Rejestr Tłumienie oferuje różne opcje ustawień, aby uwzględnić lepkie tłumienie strukturalne podczas analizy metodą liniowej analizy czasowej.
Tłumienie
Jeśli w rejestrze Basis wybrano liniową analizę implicitną Newmarka, dostępny jest tylko typ tłumienia Rayleigha. Natomiast w przypadku liniowej analizy modalnej lista oferuje dwa wybory:
- Tłumienie Lehr'a | Stałe
- Rayleigh
Gdy w liniowej analizie modalnej wybierzesz tłumienie Rayleigha, współczynniki tłumienia Rayleigha α i β zostaną skonwertowane na wartości tłumienia Lehr'a Di (patrz rozdział Parametry). Rozwiązanie jest wtedy jednoznaczne.
W przypadku tłumienia Rayleigha można automatycznie wyznaczyć parametry tłumienia z tłumienia Lehr'a. W tym celu zaznacz pole 'Obliczanie z tłumienia Lehr'a'. Następnie wprowadź parametry dwóch dominujących postaci własnych dla 'Częstotliwości własnych' f1 i f2 modelu z odpowiadającymi im wartościami dla 'Tłumienia Lehr'a' D1 i D2.
W dolnej części pokazywany jest diagram 'Częstotliwości własne - Tłumienie', który prezentuje jakie relacje zachodzą między częstością kołową własną a stałą tłumienia Lehr'a.
Parametry
W tej sekcji możesz określić parametry tłumienia. Różnią się one w zależności od rodzaju tłumienia.
Tłumienie Lehr'a
Tłumienie Lehr'a definiowane jest przez 'Stałą tłumienia Lehr'a' D. Dla każdej formy i definiuje się ją jako współczynnik między istniejącym a krytycznym tłumieniem w następujący sposób:
|
ci |
Einträge in der diagonalen Dämpfungsmatrix |
|
mi |
Modalmassen |
|
ωi |
Kreisfrequenzen des Systems |
Macierz tłumienia C musi być macierzą diagonalną.
Rayleigh
Macierz tłumienia dla tłumienia Rayleigha jest definiowana przez dwa parametry tłumienia α i β w następujący sposób:
Macierz tłumienia C dla bezpośrednich metod czasowych nie musi być koniecznie macierzą diagonalną. Dalsze informacje o tłumieniu Rayleigha można znaleźć np. w [1].
Między współczynnikami Rayleigha a tłumieniem Lehr'a istnieje następujący związek:
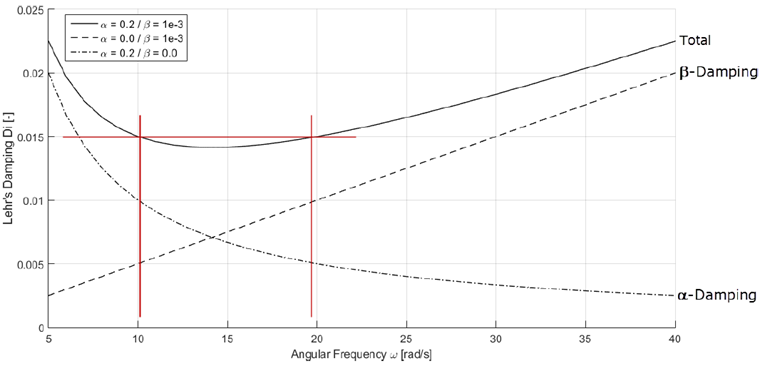
Równanie to jest przedstawione na poniższej grafice. Rozważane są różne konfiguracje dla parametrów tłumienia α = 0.2 i β = 0.001.
Dla każdej pary współczynników Rayleigha uzyskuje się różne wartości tłumienia Lehr'a. Są one zależne od częstości kołowej.