L'onglet Amortissement propose différentes options de configuration pour considérer l'amortissement structurel visqueux dans l'analyse de l'historique de temps linéaire.
Amortissement
Si vous avez sélectionné l'analyse linéaire implicite de Newmark dans l'onglet Général , seul le type d'amortissement Rayleigh est disponible. Pour la méthode d'analyse modale linéaire, deux options sont disponibles dans liste :
- Amortissement de Lehr | Constant
- Rayleigh
Lors de l'application de l'amortissement de Rayleigh à une analyse modale linéaire, les coefficients d'amortissement de Rayleigh α et β sont convertis en valeurs d'amortissement de Lehr Di (voir les paramètres). La solution est alors unique.
Dans le cas de l'amortissement de Rayleigh, il est possible de déterminer les paramètres d'amortissement automatiquement à partir de l'amortissement de Lehr. Cochez la case « Calcul à partir de l'amortissement de Lehr ». Entrez ensuite les paramètres des deux modes propres les plus dominants pour les « fréquences propres » f1 et f2 du modèle avec les valeurs correspondantes pour « l'amortissement de Lehr D1 et D2 ».
Dans la partie inférieure, le diagramme « Fréquences propres - Diagramme d'amortissement » est affiché pour l'amortissement de Rayleigh. Il représente le rapport disponible entre la fréquence angulaire propre et la constante d'amortissement de Lehr.
Paramètres
Dans cette section de la boîte de dialogue, vous pouvez définir les paramètres de l'amortissement. Elles varient selon le type d'amortissement.
Amortissement de Lehr
L'amortissement de Lehr est défini par la « constante d'amortissement de Lehr ». Il est défini pour chaque forme individuelle i comme un facteur entre l'amortissement existant et l'amortissement critique comme suit :
| ci ... | Entrées dans la matrice d'amortissement diagonale |
| mi | Masses modales |
| ωi ... | Fréquences angulaires du système structural |
La matrice d'amortissement C doit être une matrice diagonale.
Rayleigh
La matrice d'amortissement de Rayleigh est définie à l'aide des deux paramètres d'amortissement α et β comme suit :
| C | Matrice d'amortissement |
| M : | Matrice de masse |
| K | Matrice de rigidité statique |
La matrice d'amortissement C ne doit pas nécessairement être une matrice diagonale pour l'analyse directe de l'historique de temps. Vous trouverez par exemple plus d'informations sur l'amortissement de Rayleigh dans [1].
La relation suivante existe entre les coefficients de Rayleigh et l'amortissement de Lehr :
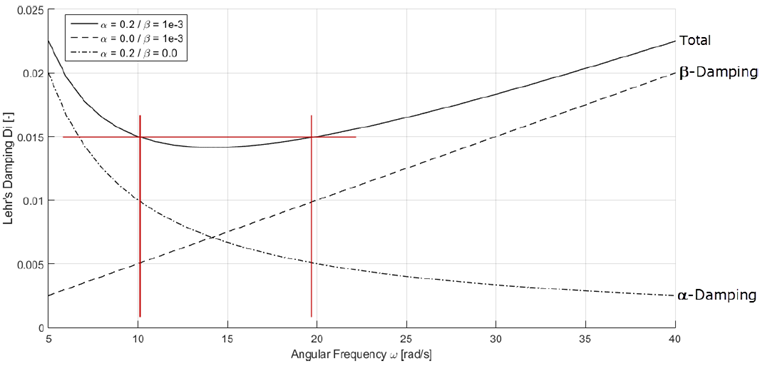
Cette équation est affichée dans le graphique suivant. Des constellations différentes pour les paramètres d'amortissement α = 0,2 et β = 0,001 sont considérées.
Des valeurs d'amortissement de Lehr différentes sont obtenues pour chaque paire de coefficients de Rayleigh. Ils dépendent de la fréquence angulaire.