O registro Amortecimento oferece várias configurações para considerar um amortecimento estrutural viscoso na análise com o método de integração direta no domínio do tempo linear.
Amortecimento
Se o método implícito de Newmark linear foi selecionado no registro Basis , apenas o tipo de amortecimento Rayleigh está disponível. No entanto, para o método de análise modal linear, a lista oferece duas opções:
- Amortecimento de Lehr | Constante
- Rayleigh
Se você aplicar o amortecimento de Rayleigh em uma análise modal linear, os coeficientes de amortecimento de Rayleigh α e β serão convertidos em valores de amortecimento de Lehr Di (veja a seção Parâmetros). A solução será então única.
No amortecimento de Rayleigh, é possível determinar automaticamente os parâmetros de amortecimento a partir do amortecimento de Lehr. Marque a opção 'Cálculo a partir do Amortecimento de Lehr'. Depois, introduza os parâmetros das duas formas próprias dominantes para as 'Frequências Próprias' f1 e f2 do modelo com os valores correspondentes para o 'Amortecimento de Lehr' D1 e D2.
Na seção inferior, o 'Diagrama de Frequências Próprias - Amortecimento' é exibido para o caso de amortecimento de Rayleigh. Ele mostra a relação entre a frequência angular própria e a constante de amortecimento de Lehr.
Parâmetros
Nesta seção, você pode definir os parâmetros de amortecimento. Eles diferem dependendo do tipo de amortecimento.
Amortecimento de Lehr
O amortecimento de Lehr é definido através da 'Constante de Amortecimento de Lehr' D. Ela é definida para cada forma i como um fator entre o amortecimento existente e o crítico da seguinte forma:
|
ci |
Entradas na matriz de amortecimento diagonal |
|
mi |
Massas modais |
|
ωi |
Frequências angulares naturais do sistema |
A matriz de amortecimento C deve ser uma matriz diagonal.
Rayleigh
A matriz de amortecimento de Rayleigh é definida pelos dois parâmetros de amortecimento α e β da seguinte forma:
|
C |
Matriz de amortecimento |
|
M |
Matriz de massas |
|
K |
Matriz de rigidez estática |
A matriz de amortecimento C não precisa obrigatoriamente ser uma matriz diagonal para os métodos de integração direta no domínio do tempo. Mais informações sobre o amortecimento de Rayleigh podem ser encontradas, por exemplo, em [1].
Existe a seguinte relação entre os coeficientes de Rayleigh e o amortecimento de Lehr:
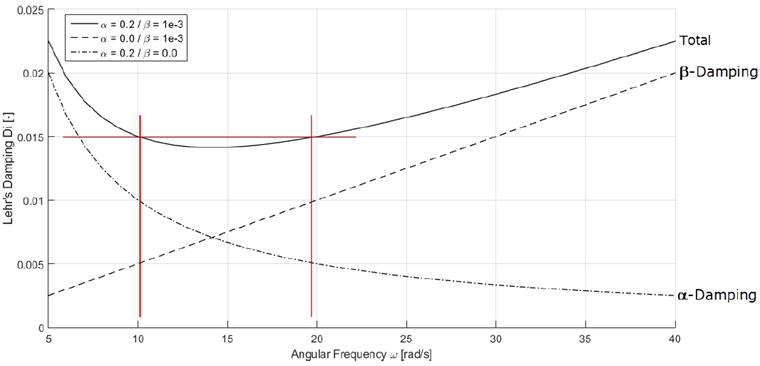
Essa equação é ilustrada no gráfico a seguir. Diferentes configurações dos parâmetros de amortecimento α = 0.2 e β = 0.001 são consideradas.
Para cada par de coeficientes de Rayleigh, são obtidos diferentes valores de amortecimento de Lehr. Eles dependem da frequência angular.