La pestaña Amortiguamiento ofrece varias opciones de configuración para considerar el amortiguamiento estructural viscoso en el análisis utilizando el análisis lineal en el dominio del tiempo.
Amortiguamiento
En la pestaña Datos básicos , el análisis lineal implícito de Newmark solo está disponible para el 'Tipo de amortiguamiento' Rayleigh. Para el método de análisis modal lineal, por otro lado, la lista proporciona dos opciones:
- Amortiguamiento de Lehr | Constante
- Rayleigh
Al aplicar el amortiguamiento de Rayleigh a un análisis modal lineal, los coeficientes de amortiguamiento de Rayleigh α y β se convierten en valores de amortiguamiento de Lehr Di (consulte el párrafo Parámetro). La solución es entonces única.
En el caso del amortiguamiento de Rayleigh, es posible determinar los parámetros de amortiguamiento automáticamente a partir del amortiguamiento de Lehr. Seleccione la casilla 'Cálculo a partir del amortiguamiento de Lehr'. Luego, introduzca los parámetros de las dos deformadas del modo más dominantes para las 'Frecuencias naturales' f1 y f2 del modelo con los valores correspondientes para el 'Amortiguamiento de Lehr' D1 y D2.
En la sección inferior, se muestra el 'Diagrama frecuencias naturales-Amortiguamiento' para el amortiguamiento de Rayleigh. Representa la relación que está disponible entre la frecuencia angular natural y la constante de amortiguamiento de Lehr.
Parámetros
En esta sección del diálogo, puede definir los parámetros del amortiguamiento. Difieren según el tipo de amortiguamiento.
Amortiguamiento de Lehr
El amortiguamiento de Lehr se define mediante la 'Constante del amortiguamiento de Lehr' D. Se define para cada forma individual i como un factor entre el amortiguamiento existente y el crítico de la siguiente manera:
| ci | Entradas en la matriz de amortiguamiento diagonal |
| mi | Masas modales |
| ωi | Frecuencias angulares del sistema estructural |
La matriz de amortiguamiento C debe ser una matriz diagonal.
Rayleigh
La matriz de amortiguamiento del amortiguamiento de Rayleigh se define por medio de los dos parámetros de amortiguamiento α y β como sigue:
| C | Matriz de amortiguamiento |
| M | Matriz de masas |
| K | Matriz de rigidez estática |
La matriz de amortiguamiento C no tiene que ser necesariamente una matriz diagonal para el análisis directo en el dominio del tiempo. Puede encontrar más información sobre el amortiguamiento de Rayleigh en [1], por ejemplo.
Existe la siguiente relación entre los coeficientes de Rayleigh y el amortiguamiento de Lehr:
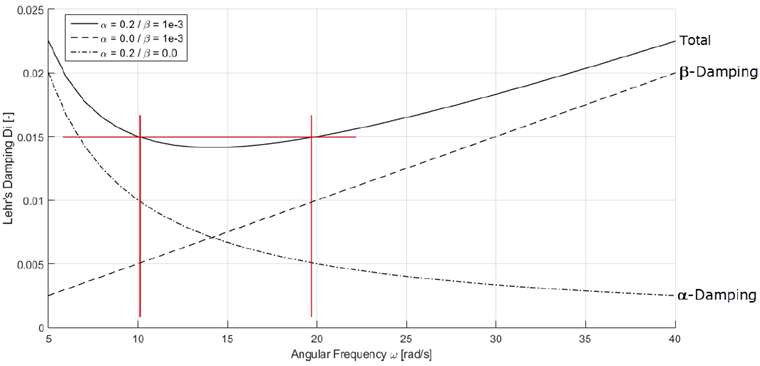
Esta ecuación se muestra en el siguiente gráfico. Se consideran diferentes constelaciones para los parámetros de amortiguamiento α = 0.2 y β = 0.001.
Para cada par de coeficientes de Rayleigh resultan valores de amortiguamiento de Lehr diferentes. Dependen de la frecuencia angular.