Nonlinear Analysis in RF-/CONCRETE

Back to Knowledge Base

Figure 01 - System and Loading

Figure 02 - Window '3.1 Provided Longitudinal Reinforcement' in CONCRETE

Figure 03 - Window '1.1 General Data' for Serviceability Limit State with Settings for Nonlinear Calculation According to [2]

Figure 04 - Window '1.3 Cross-Sections' with Settings for Creep and Shrinkage

Figure 05 - Window '6.2.3 Serviceability Limit State for Nonlinear Calculation by Member'

Figure 06 - Comparison of Deformations

Figure 07 - Distribution of Stiffness Iym ∙ E

Technical Article

This article was translated by Google Translator View original text

001488

10/23/2017

Technical Article Robert Vogl Add-on Modules RFEM RSTAB RF-CONCRETE CONCRETE RF-CONCRETE NL EC2 for RFEM/RSTAB Concrete Structures Nonlinear Analysis Eurocode 2

When designing reinforced concrete components according to EN 1992-1-1, [1] nonlinear methods of determining internal forces are possible for the ultimate and serviceability limit states. The internal forces and deformations are determined while taking the nonlinear behavior of internal forces and deformations into account. The calculation of stresses and strains in the cracked state generally results in deflections that are considerably higher than the linearly determined values.

A previous article describes general methods for the calculation and modeling of downstand beams, ribs, and slabs in the cracked state. The following descriptions describe the design of a continuous reinforced concrete beam. The calculation is possible with the modules CONCRETE and RF-CONCRETE Members in combination with licenses for EC2 and RF-CONCRETE NL.

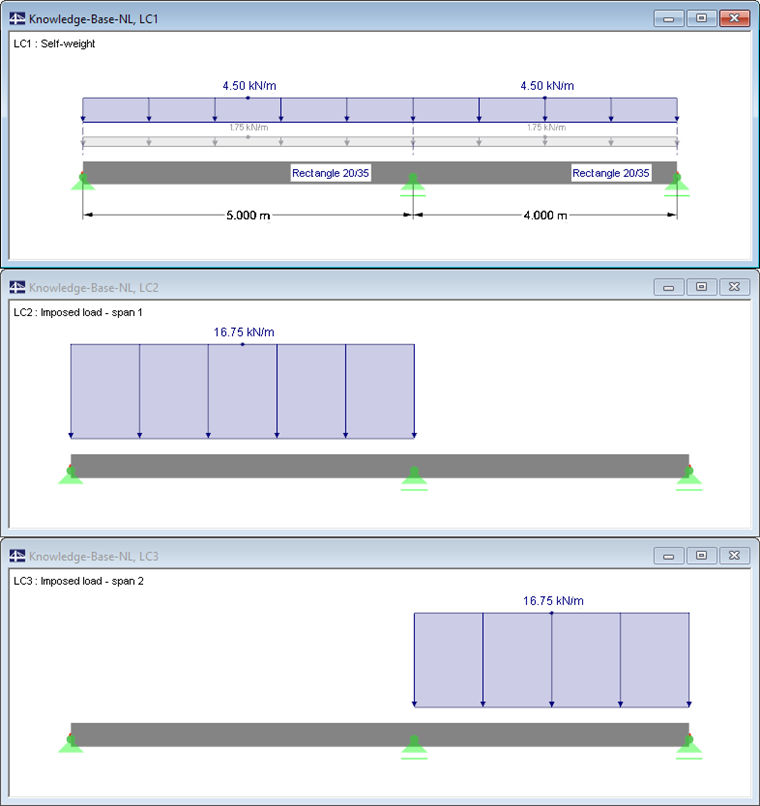
System and Loading

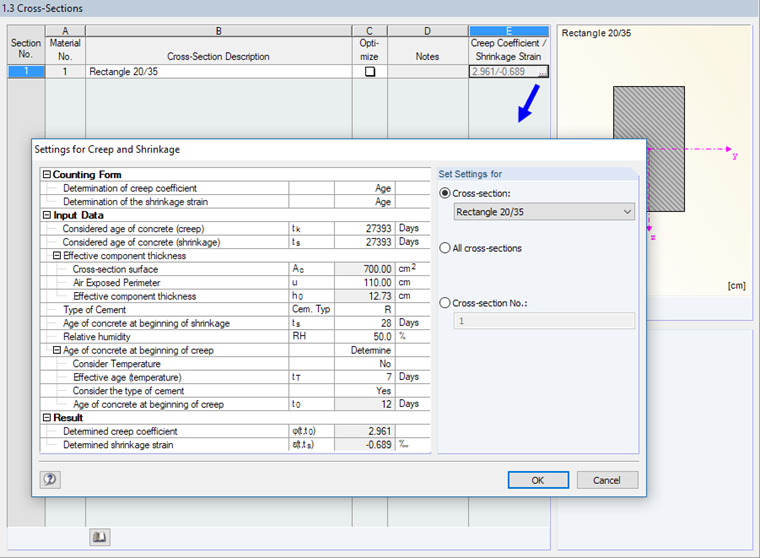
The continuous beam consists of a rectangular cross-section 20/35 cm with the concrete grade C30/37.

The permanent loads and traffic loads are organized in three load cases. For the determination of the design combinations according to EN 1990, RFEM/RSTAB uses the automatic combinatorics for ultimate and serviceability (common design situation).

Figure 01 - System and Loading

Linear Calculation of Reinforcement in ULS

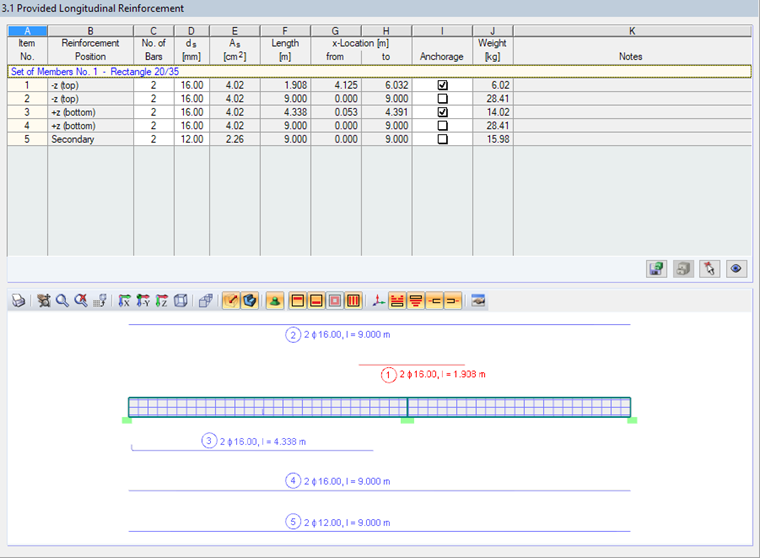
First, the reinforcement for the ultimate limit state is determined. The calculation is carried out taking into account the moment redistribution and rounding for the internal forces of the result combination RC1. Furthermore, the following reinforcement parameters are specified:

Reinforcement diameter 16 mm
Reinforcement scaling for three areas
Concrete cover 30 mm
Minimum reinforcement 2 Ø 12 for top and bottom layer
Structural reinforcement for a maximum reinforcement spacing of 15 cm with Ø 12

Based on these specifications, the program determines a reinforcement proposal according to the linear-elastic approach. In Window 3.1, you can check the reinforcement, which is the basis for the nonlinear calculation.

Figure 02 - Window '3.1 Provided Longitudinal Reinforcement' in CONCRETE

Nonlinear Calculation of Crack Widths and Deformations in SLS

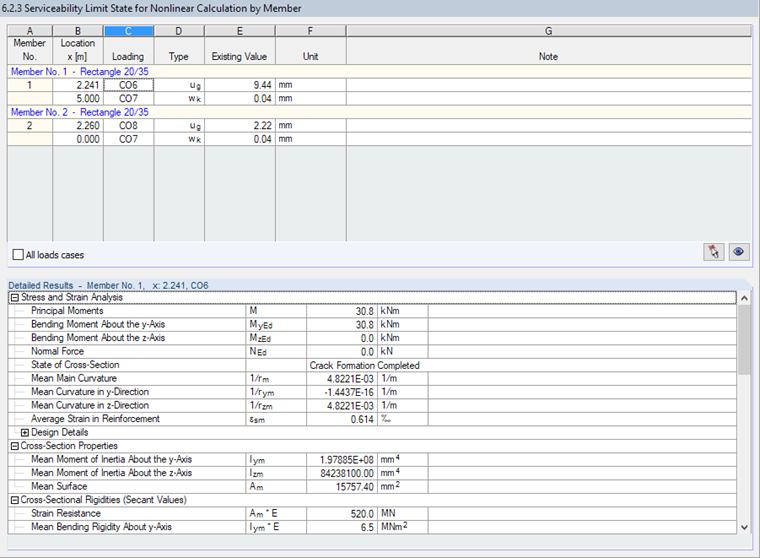
The nonlinear calculation for the serviceability limit state is performed for the load combinations CO6 to CO8 (result combinations do not allow for clear stress-strain relations). The effects of tension stiffening should be included in the nonlinear analysis. For this, the approach with modified steel characteristic according to [2] is selected.

Figure 03 - Window '1.1 General Data' for Serviceability Limit State with Settings for Nonlinear Calculation According to [2]

In addition, the effects of creep and shrinkage are taken into account. The specifications are made in window 1.3.

Figure 04 - Window '1.3 Cross-Sections' with Settings for Creep and Shrinkage

Results

A physical and geometric nonlinear calculation is performed. The iteration of the state of strain state is done on the cross-section plane. Starting from a distribution of internal forces within an iteration cycle, new and current strain-stress states are always calculated. The convergence is reached when an equilibrium state is reached.

As expected, the maximum deformations occur in field 1 for the loading of CO6 (LC1 + 0.5 ∙ LC2). The crack widths are small.

Figure 05 - Window '6.2.3 Serviceability Limit State for Nonlinear Calculation by Member'

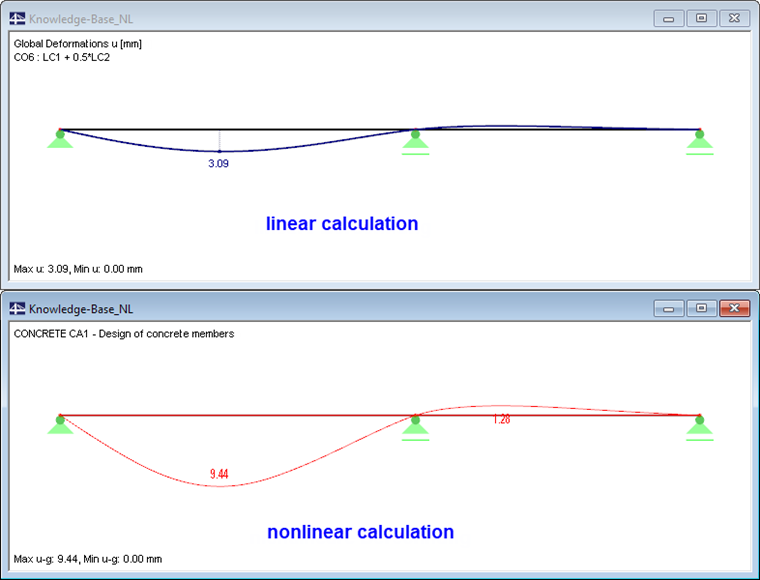
The deformation from the nonlinear calculation with consideration of the creep effect is significantly higher than the deformation of the purely linear elastic calculation without creep influence. This can be clearly seen in a comparison of the deformations.

Figure 06 - Comparison of Deformations

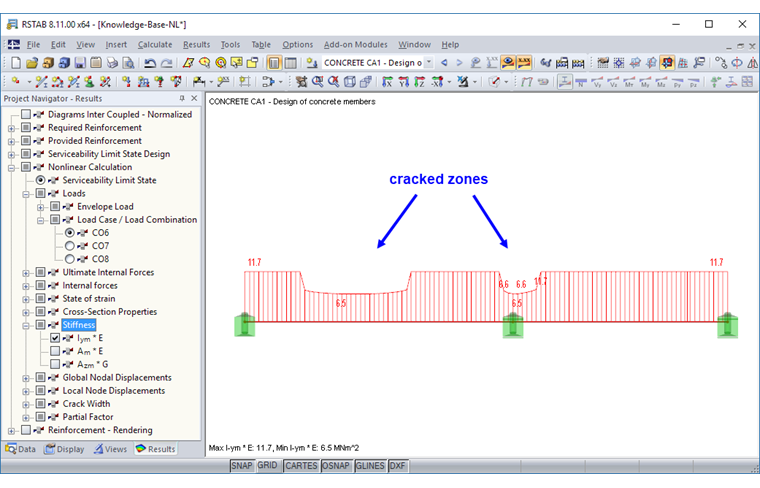
The stiffness diagram shows that a large area of panel 1 is cracked in the service state.

Figure 07 - Distribution of Stiffness Iym ∙ E

Summary

Compared to a linear-elastic calculation of reinforced concrete components, the nonlinear analysis of stiffnesses and strains provides deformation values that can be significantly higher when considering crack formation. This effect can be taken into account with the nonlinear analysis methods of the Dlubal reinforced concrete modules. It is also possible to consider the influence of creep and shrinkage.

Reference

[1]	Eurocode 2: Design of reinforced concrete and prestressed concrete structures - Part 1‑1: General rules and rules for buildings; EN 1992‑1‑1: 2004 + AC: 2010
[2]	DAfStb: DAfStb Issue 525 - Explanations of DIN 1045: 1. Berlin: Beuth, 2003
[3]	Manual CONCRETE. Tiefenbach: Dlubal Software, August 2017. Download

Keywords

Nonlinear method Cracked state State II (cracked) Crack width cracking Serviceability tension stiffening Creep Shrinkage State of strain Stiffness

Downloads

RSTAB Model File

Contact us

Contact Dlubal Software

Do you have questions or need advice?
Contact our free e-mail, chat, or forum support or find various suggested solutions and useful tips on our FAQ page.