Symbols Used
| L | Beam length |
| b | Beam width |
| h | Beam height |
| E | Modulus of elasticity |
| G | Shear Modulus |
| Iz | Second moment of area about the weak axis |
| IT | Torsion moment of inertia |
| az | Load application distance from the shear center |
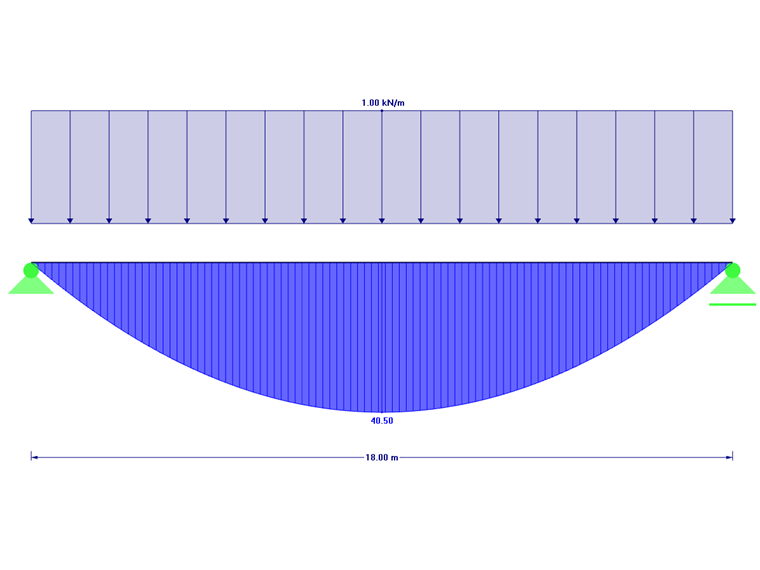
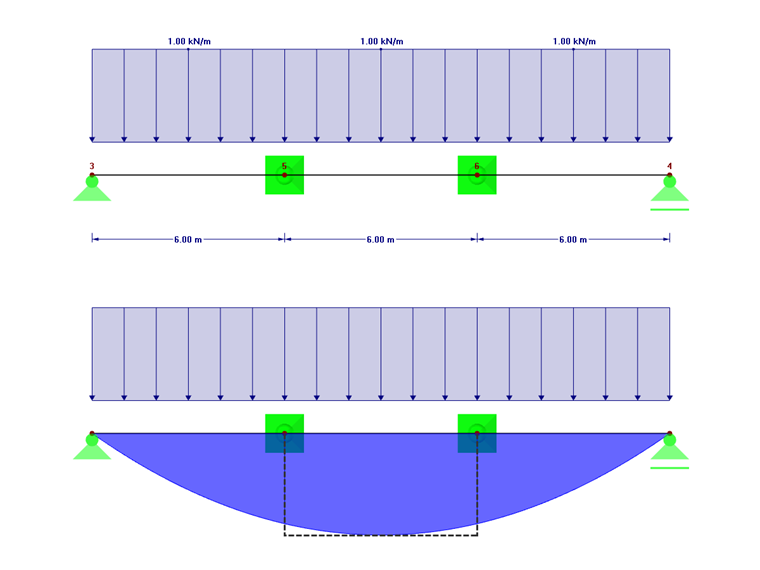
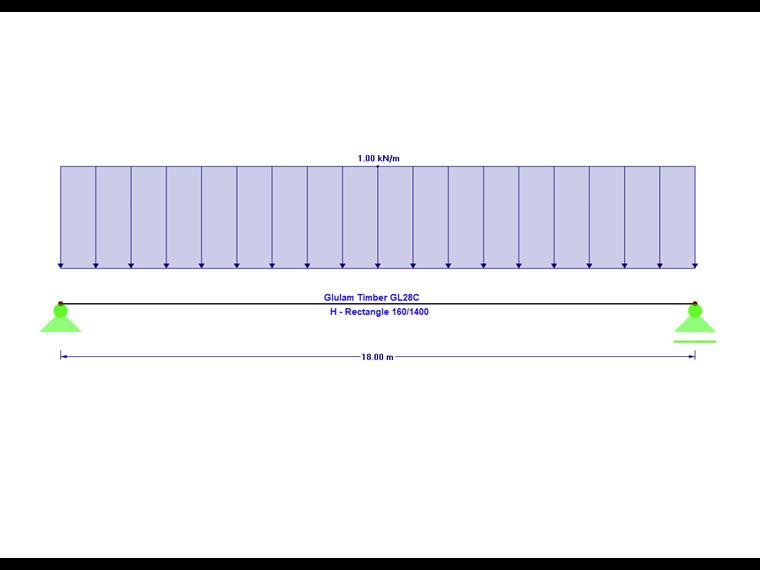
Single-Span Beam with Lateral and Torsional Restraint and Without Intermediate Support
| L | 18 | m |
| b | 160 | mm |
| h | 1.400 | mm |
| az | 700 | mm |
| Iz | 477.866.667 | mm4 |
| IT | 1.773.842.967 | mm4 |
| E0.05 | 10.400 | N/mm² |
| G0,05 | 540 | N/mm² |
For the single-span beam with lateral and torsional restraint without intermediate supports (see Image 01), the equivalent member length results in the case of a load application at the top to:
The factors a1 and a2 can be seen in Image 02 according to the moment distribution.
The critical bending moment can then be calculated as follows:
In this example, we do not increase the product of the 5% quantiles of the stiffness values due to the homogenization of beams made of glued-laminated timber.
For more complex systems, it may be advantageous to determine the critical loads, moments, or stresses using the eigenvalue solver. Use the RF-/FE-LTB add-on module, which is based on the finite element method, to calculate the stability loads of sets of members. An elastic material behavior is assumed for a geometric nonlinear behavior. The critical load factor is important for timber construction. This indicates the factor by which the load can be multiplied before the system becomes unstable.
For this example, the beam is loaded with a unit load of 1 kN/m. For this, the bending moment results in:
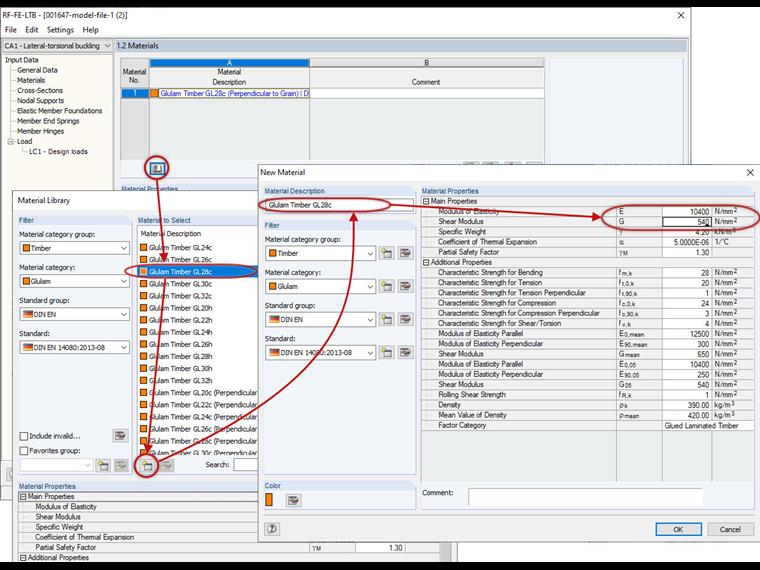
Since the lower quantile value of the critical moment is to be determined, the 5% quantiles must be used for the stiffness values E and G. To do this, you have to create a user-defined material that is only used in the add-on module. For this material, the stiffness parameters E and G have to be replaced.
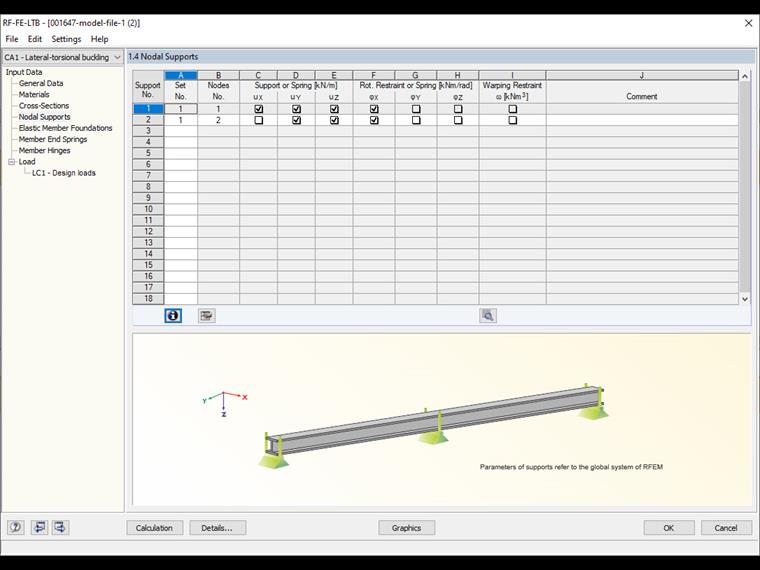
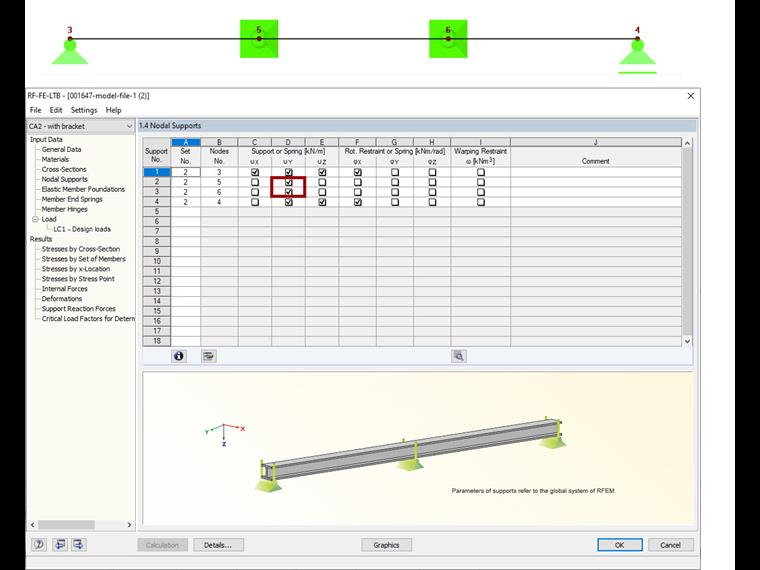
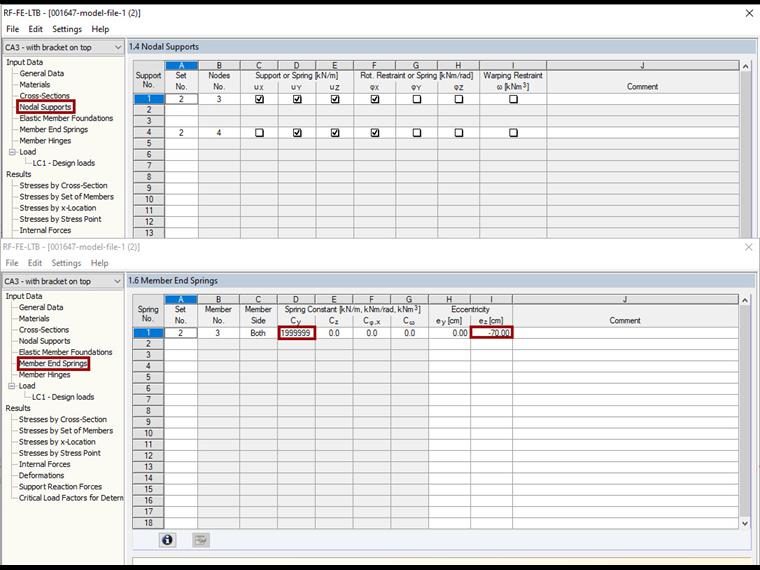
Then, define the lateral and torsional restraints. It is important to ensure that the degree of freedom φZ also needs to be solved.
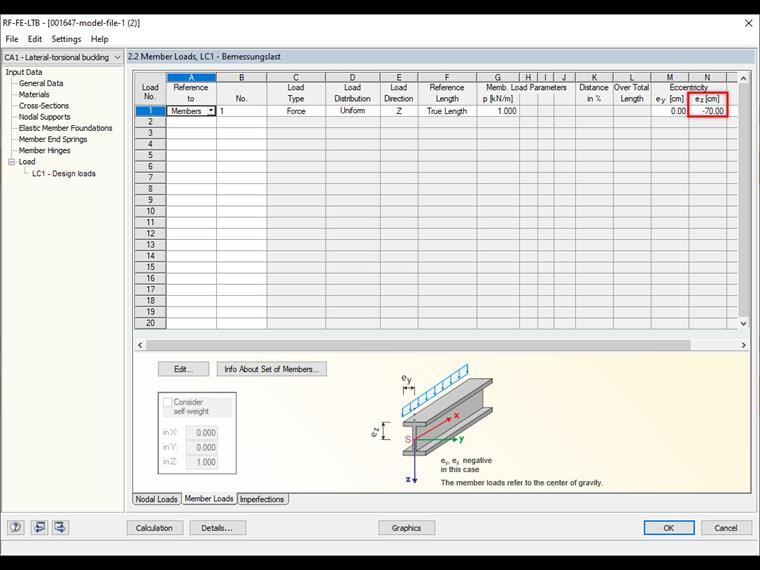
You have to set the load eccentrically so that it acts on top of the beam.
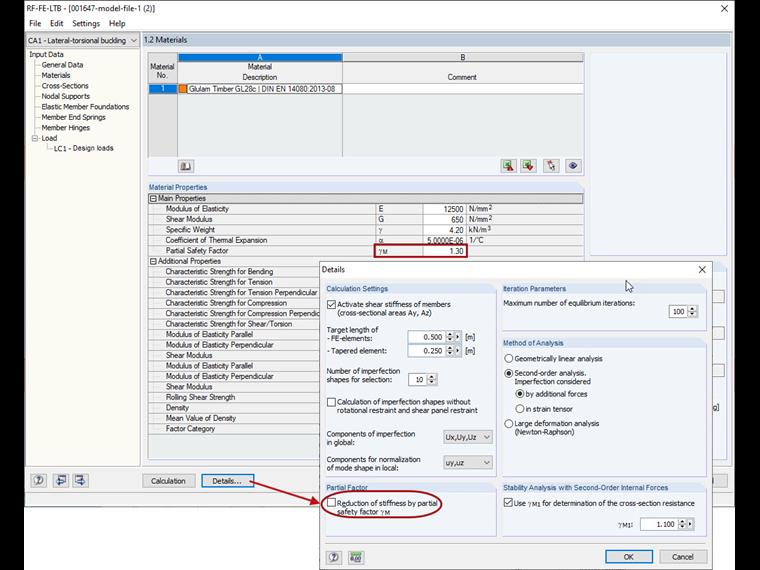
In the details, it is still necessary to deactivate the reduction of the stiffness by the partial safety factor γM (see Image 07). Alternatively, you can set the partial safety factor to 1.0 directly in the user-defined material.
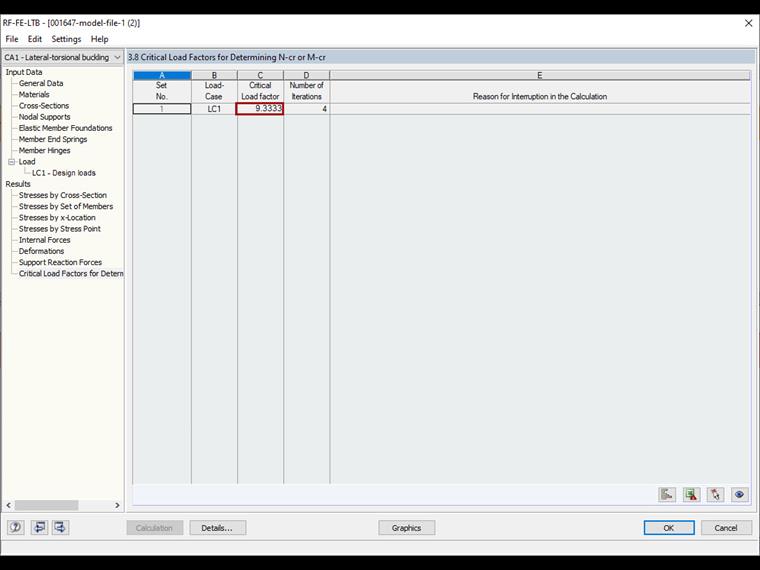
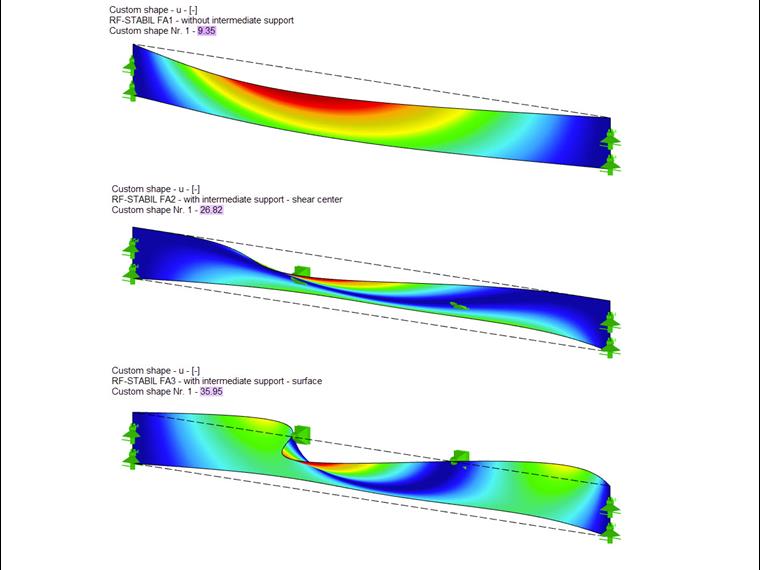
The calculation results in a critical load factor of 9.3333 (see Image 08). If the load is multiplied by this factor, the upper flange will deflect and the system becomes unstable.
The following applies for the critical moment:
This corresponds very well with the result of the analytical solution.
Single-Span Beam with Lateral and Torsional Restraint and Intermediate Support
The beam is now supported as rigidly fixed laterally at the third points by a stiffening structure.
Since the moment distribution in the middle area is almost constant, a constant moment distribution is assumed for the lateral buckling length coefficient. Thus, the value of a1 is 1.0 and a2 is 0. The effective length with L = 6.0 m results in
and the critical moment in
The eigenvalue solver results in a critical load factor of 26.1735, taking into account the intermediate supports at the shear center (see Image 10).
The following applies for the critical moment:
If the intermediate support acts on the upper side (see Image 11), the critical load factor becomes larger (32.5325), because this position has a more favorable effect on the lateral buckling behavior of the beam.
The analytical approximation is also relatively good for this case.
Alternative Analysis on a Surface Model
You can also use RFEM and the RF‑STABILITY add-on module to calculate the critical load factors. For this, it is necessary that you model the beam as an orthotropic surface. The results from RF‑STABILITY correspond very well to the member calculation from RF‑/FE‑LTB. The first mode shape and the corresponding critical load factor are shown in Image 12.
| System | Mcrit analytical | Mcrit RF-/FE-LTB | Mcrit RF-STABILITY |
|---|---|---|---|
| Without Intermediate Support | 375.42 kNm | 378.00 kNm | 378.55 kNm |
| With Intermediate Support in Shear Center | 1,142.41 kNm | 1,060.03 kNm | 1,085.81 kNm |
| With Intermediate Support on Top Chord | - | 1,317.57 kNm | 1,455.98 kNm |
In most cases, it is probably sufficient to determine the critical bending moment Mcrit or the critical bending stress σcrit using the analytical equations from the literature. For special cases, two options for implementation using Dlubal programs were shown. While the RF‑/FE‑LTB add-on module is used to perform the calculation using members, the RF‑STABILITY add-on module allows you to perform even more complex stability designs. One example is a lateral and torsional restraint that is not arranged over the entire beam height. This can be analyzed easily with a surface model.
.png?mw=760&hash=7dfb9668b098804bdded20f2b0205bbc97b03faa)