9814x

001647

Dipl.-Ing. (FH) Gerhard Rehm

17.7.2020

Klopení dřevěných konstrukcí | Příklady 1

V článku Klopení dřevěných konstrukcí | Teorie přibližujeme teoretická východiska pro analytickou metodu stanovení kritického ohybového momentu M_crit, respektive kritického ohybového napětí σ_crit pro klopení ohybového nosníku. V následujícím příspěvku na příkladech ověříme analytické řešení výsledkem analýzy vlastních čísel.

Použité symboly

L	Délka nosníku
b	Šířka nosníku
h	Výška nosníku
E	modul pružnosti
G	Smykový modul
Iz	moment setrvačnosti okolo hlavní osy nejmenší tuhosti
IT	Moment tuhosti v prostém kroucení
az	vzdálenost působiště zatížení od středu smyku

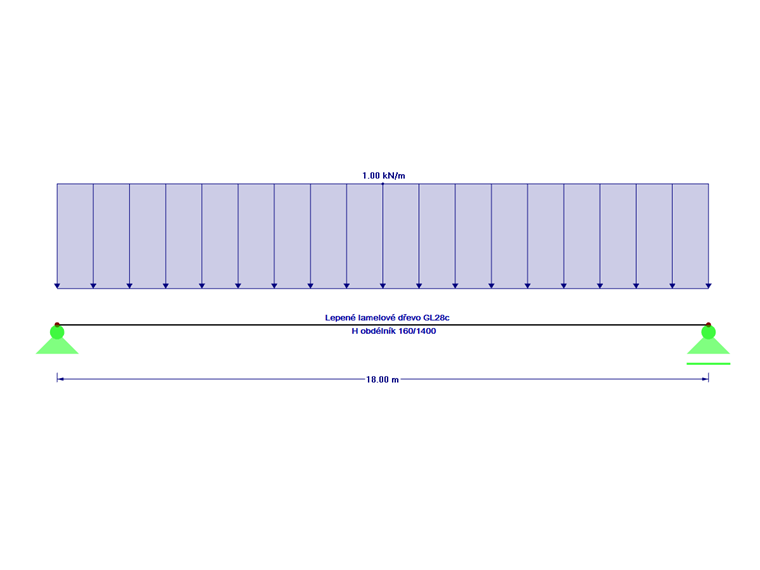
Prostý nosník s vidlicovým uložením bez mezilehlých podpor

L	18	m
b	160	mm
h	1 400	mm
az	700	mm
Iz	477.866.667	mm⁴
IT	1.773.842.967	mm⁴
E0,05	10 400	N/mm²
G0,05	540	N/mm²

Prostý nosník s vidlicovým uložením bez mezilehlých podpor

U prostého nosníku s vidlicovým uložením bez mezilehlých podpor (viz obr. 01) se délka náhradního prutu při působení zatížení na horní straně stanoví ze vztahu:

l_{ef} = \frac{L}{a_{1} \cdot [1 - a_{2} \cdot \frac{a_{z}}{L} \cdot \sqrt{\frac{{EI}_{z}}{{GI}_{T}}}]} = 18.26 m

délka náhradního prutu

Die Faktoren a₁ und a₂ können Bild 02 entsprechend dem Momentenverlauf entnommen werden.

Součinitele klopení

Kritický ohybový moment lze pak spočítat následovně:

M_{crit} = \frac{π \cdot \sqrt{E_{0, 05} \cdot I_{z} \cdot G_{0, 05} \cdot I_{T}}}{l_{ef}} = 375, 42 kNm

Vzorec 2

V našem příkladu nebudeme uvažovat zvýšení součinu 5% kvantilů tuhosti v důsledku homogenizace nosníků z lepeného lamelového dřeva.

U složitějších systémů může být výhodné použít pro stanovení kritických zatížení, momentů nebo napětí řešič vlastních čísel. Přídavný modul RF-/FE-LTB umožňuje vypočítat kritická zatížení u sad prutů metodou konečných prvků. Přitom se pro geometricky nelineární chování předpokládá pružné chování materiálu. Důležitým výsledkem pro dřevěné konstrukce je součinitel kritického zatížení, který udává, jakým součinitelem lze zatížení vynásobit, než dojde ke ztrátě stability konstrukce.

Přídavný modul RF-FE-LTB pro RFEM 5

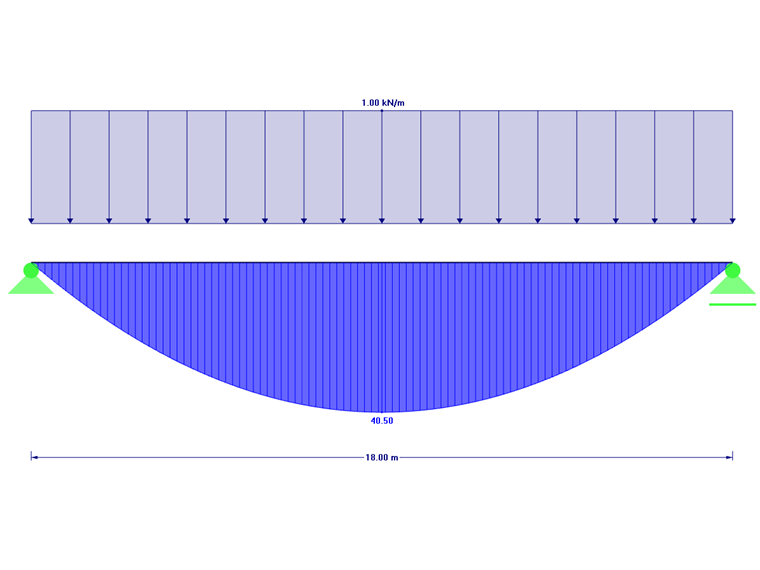
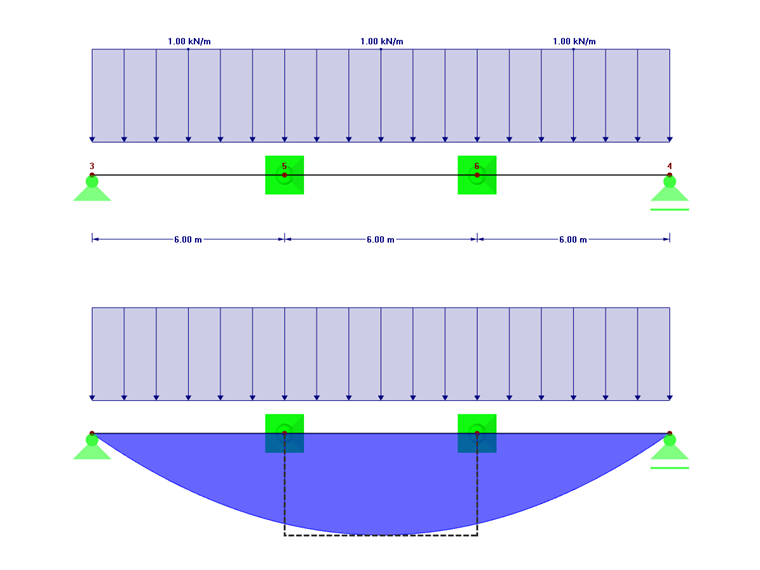
V našem příkladu zatížíme nosník jednotkovým zatížením 1 kN/m. Výsledkem je tak následující ohybový moment:

M = \frac{q \cdot L^{2}}{8} = \frac{1, 00 \cdot 18, 00^{2}}{8} = 40, 50 kNm

Vzorec 3

Průběh momentů na prostém nosníku při jednotkovém zatížení

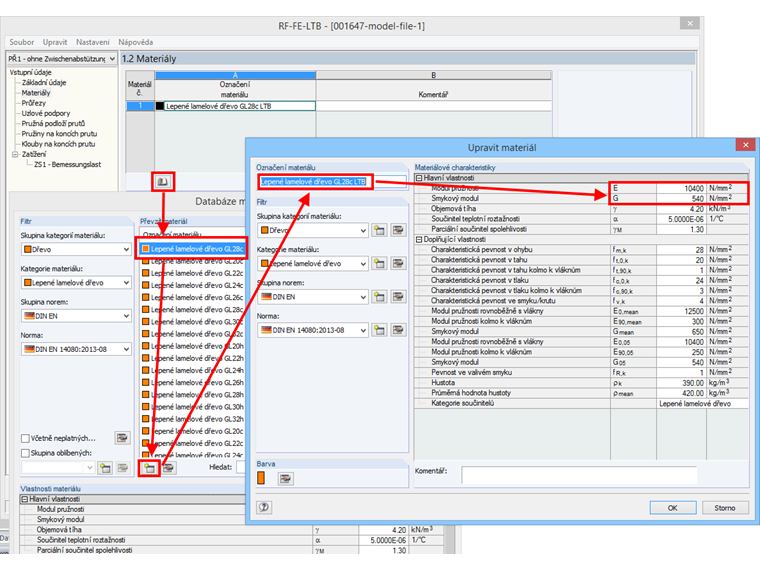
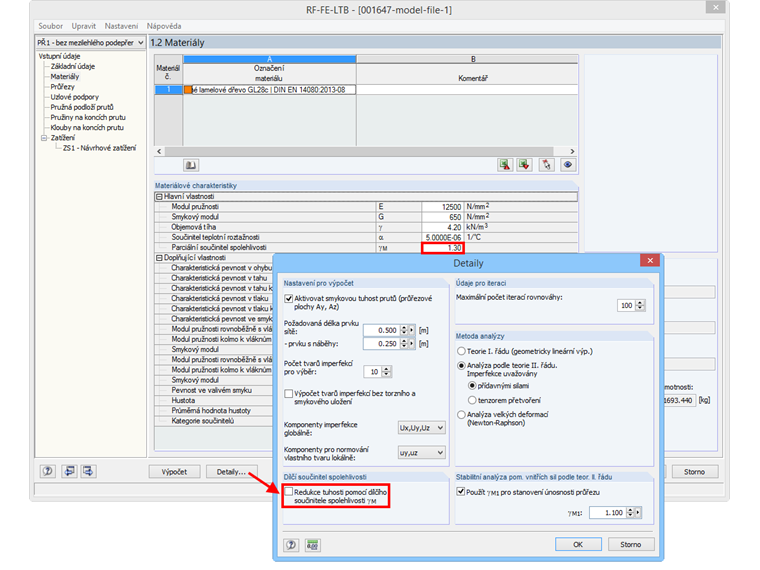
Protože se má stanovit dolní kvantil kritického momentu, použijí se pro hodnoty tuhosti E a G 5% kvantily. K tomu je třeba vytvořit uživatelsky definovaný materiál, který se použije pouze v tomto přídavném modulu. U daného materiálu nahradíme příslušné hodnoty tuhosti E a G.

Vytvoření uživatelsky definovaného materiálu

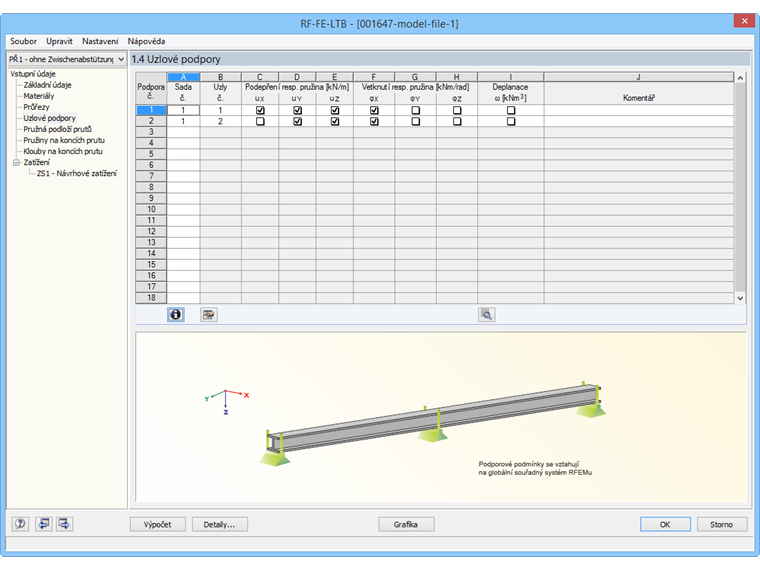
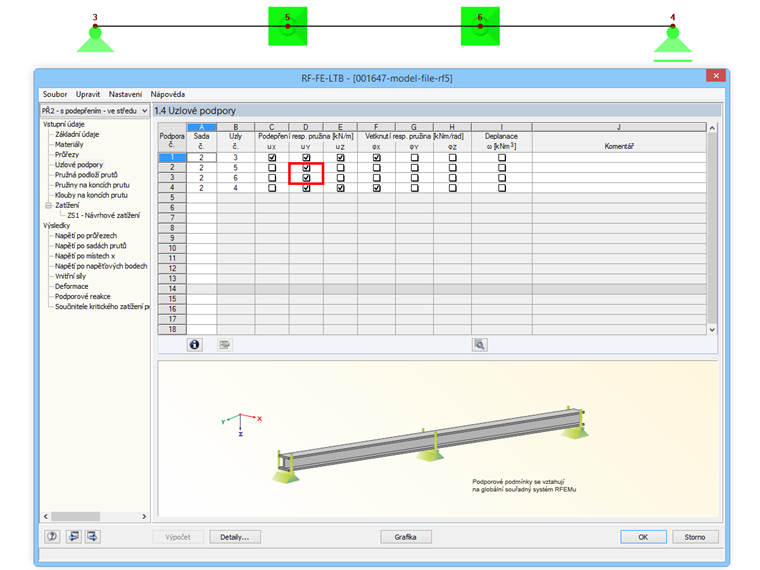
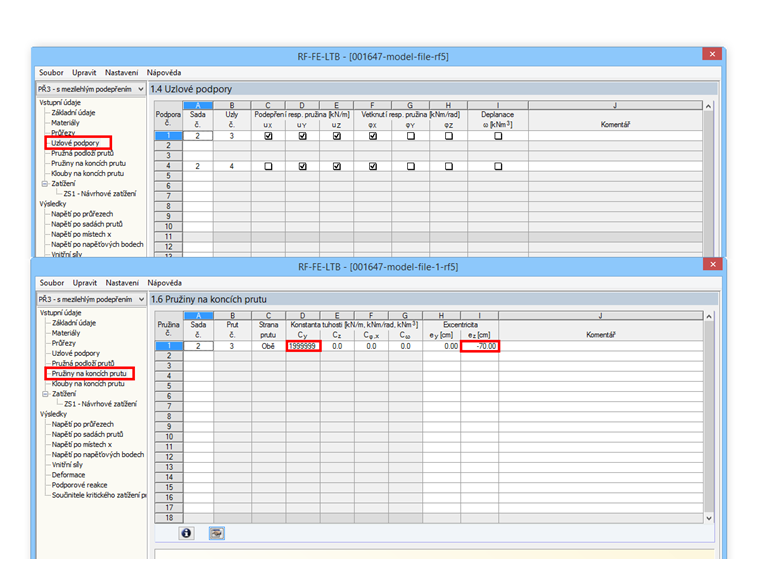
Následně zadáme vidlicové uložení. Přitom je důležité uvolnit také stupeň volnosti φ_Z.

Zadání podporových podmínek

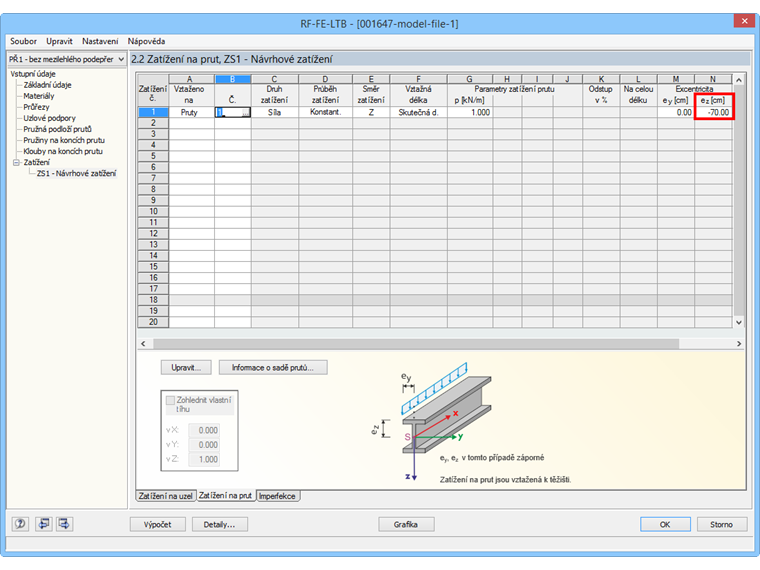
Aby zatížení působilo na horní část nosníku, je třeba ho zadat s excentricitou.

Excentrické působení zatížení

V detailech pak ještě musíme deaktivovat volbu pro redukci tuhosti dílčím součinitelem spolehlivosti γ_M (viz obr. 07), případně můžeme u materiálu zadaného uživatelem nastavit dílčí součinitel spolehlivosti na 1,0.

Detaily v RF-/FE-LTB

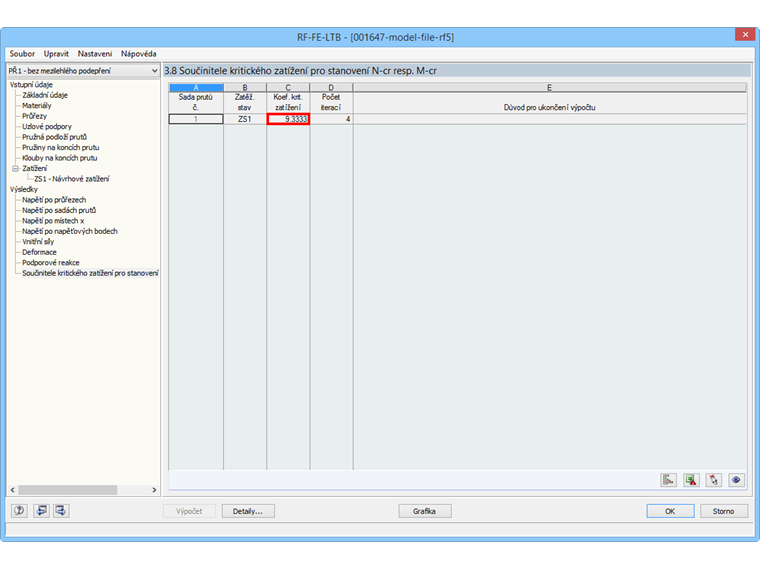
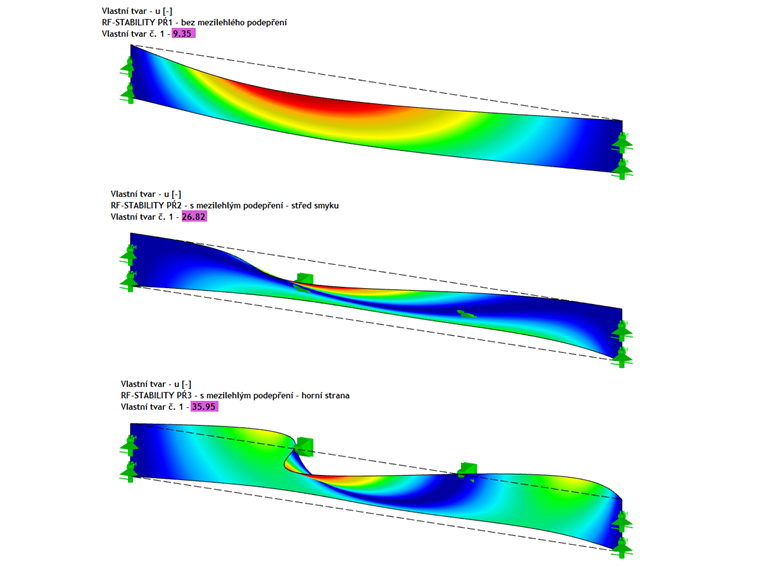
Výsledkem výpočtu je součinitel kritického zatížení 9,3333 (viz obr. 08). Pokud se zatížení vynásobí tímto součinitelem, dojde k vybočení horní pásnice a ztrátě stability systému.

Součinitel kritického zatížení

Pro kritický moment pak platí:

M_{crit} = 9, 3333 \cdot 40, 50 kNm = 378, 00 kNm

Vzorec 4

Tento výsledek odpovídá výsledku analytického řešení.

Prostý nosník s vidlicovým uložením s mezilehlým podepřením

Nosník je ve třetinách podepřen proti příčnému posunutí.

Průběh ohybového momentu ve středu pole

Vzhledem k tomu, že průběh momentů ve střední oblasti je téměř konstantní, bude se pro součinitele vzpěrné délky při klopení uvažovat konstantní průběh momentů. Hodnota a₁ je tudíž 1,0 a hodnota a₂ je 0. Vzpěrná délka je tak při L = 6,0 m

l_{ef} = \frac{L}{a_{1} \cdot [1 - a_{2} \cdot \frac{a_{z}}{L} \cdot \sqrt{\frac{{EI}_{z}}{{GI}_{T}}}]} = 6, 00 m

Vzorec 5

a kritický moment

M_{crit} = \frac{π \cdot \sqrt{E_{0, 05} \cdot I_{z} \cdot G_{0, 05} \cdot I_{T}}}{l_{ef}} = 1142, 41 kNm

Vzorec 6

Analýzou vlastních čísel se při zohlednění mezilehlého podepření ve středu smyku (viz obr. 10) stanoví součinitel kritického zatížení 26,1735.

Zadání podpor proti příčnému posunutí

Pro kritický moment pak platí:

M_{crit} = 26, 1735 \cdot 40, 50 kNm = 1060, 03 kNm

Vzorec 7

Pokud působí mezilehlé podepření na horní straně (viz obr. 11), pak je součinitel kritického zatížení větší (32,5325), protože toto umístění má příznivější vliv na stabilitní chování nosníku.

M_{crit} = 32, 5325 \cdot 40, 50 kNm = 1317, 57 kNm

Vzorec 8

Zadání excentrického podepření

I v tomto případě přináší přibližné řešení analytickou metodou poměrně dobrý výsledek.

Analýza plošného modelu jako alternativní řešení

Součinitele kritického zatížení lze vypočítat také pomocí programu RFEM a přídavného modulu RF-STABILITY. K tomu je třeba modelovat nosník jako ortotropní plochu. Výsledky z modulu RF-STABILITY velmi dobře odpovídají výpočtu prutu v modulu RF-/FE-LTB. První vlastní tvar a příslušný součinitel kritického zatížení jsou znázorněny na obr. 12.

Přídavný modul RF-STABILITY pro RFEM 5

Vlastní tvary plošného modelu s příslušným součinitelem kritického zatížení

Systém	M_crit analytisch	M_crit RF-/FE-BGDK	M_crit RF-STABIL
bez mezilehlých podpor	375,42 kNm	378,00 kNm	378,55 kNm
s mezilehlým podepřením ve středu smyku	1.142,41kNm	1 060,03 kNm	1 085,81 kNm
mit Zwischenabstützung am Obergurt	-	1 317,57 kNm	1 455,98 kNm

Ve většině případů pravděpodobně stačí určit kritický ohybový moment M_crit, resp. kritické ohybové napětí σ_crit pomocí analytických rovnic z odborných příruček. Pro zvláštní případy jsme předvedli dvě možnosti, k nimž můžeme využít programy Dlubal. Während mit dem Zusatzmodul RF-/FE-BGDK,die Berechnung mittels Stäben erfolgt, können mit dem Zusatzmodul RF-STABIL noch komplexere Stabilitätsbetrachtungen durchgeführt werden. Jako příklad jsme uvedli vidlicové uložení, které není uspořádáno po celé výšce nosníku. Takový případ lze snadno posoudit pomocí plošného modelu.

Databáze znalostí

KB 001647 | Klopení dřevěných konstrukcí | Příklady 1

Autor

Ing. Rehm se podílí na vývoji programů pro dřevěné konstrukce a zajišťuje technickou podporu zákazníkům.

Odkazy

Stahování

Model | Soubor RFEM 5

1,96 MB

Model | Soubor RSTAB 8

1,96 MB

;