Nonlinear Reinforced Concrete Analysis – General Method for Stability Analysis According to DIN EN 1992-1-1

General Method for Stability Analysis According to DIN EN 1992-1-1 in RFEM 6

Theoretical Background

The general method according to 5.8.6 imposes the following additional requirements on analysis and design.

Geometric Nonlinearity - Second-Order Theory

According to subsection 5.8.6(1), geometric nonlinearities must be considered. Consequently, internal forces are determined on the deformed system according to the second-order theory taking into account imperfections.

Physical Nonlinearity - Material

The general rules for nonlinear methods according to 5.7 still apply. Subsection 5.7(1) states that "nonlinearities of construction materials must be appropriately considered." According to 5.7(4)P, when using nonlinear methods, material properties that lead to realistic stiffness and account for uncertainties in failure must be used.

Thus, appropriate stress-strain curves for concrete and reinforcing steel are to be used.

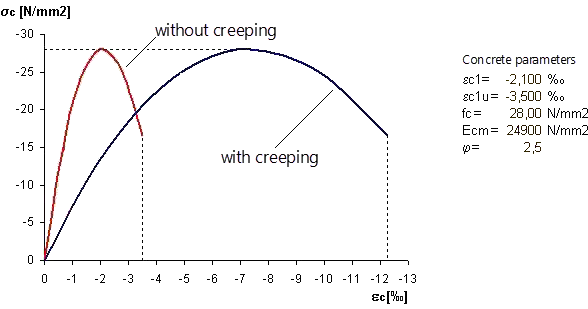
• Creep Deformation

Creep must be considered and may be applied using a modified stress-strain curve according to 5.8.6 (3). For this, the strain values of concrete are multiplied by the factor (1 + ϕ_ef), where ϕ_ef is the effective creep coefficient according to 5.8.4. The procedure is exemplary shown in the following image.

Distortion of Stress-Strain Curve in Reinforced Concrete

• Tension Stiffening

The involvement of concrete between cracks (Tension Stiffening) may be considered. For this, an appropriate method, either using a suitable concrete curve for the tensile area (1 in the image below) or through a modified reinforcement steel curve (2 in the image below), is to be chosen.

Considering Tension Stiffening Effect in RFEM

Safety Concept

• Internal Forces and Deformations

According to EN 1992-1-1, Section 5.8.6 (NDP 5.8.6 (3)), internal forces and deformations may be determined using mean material properties (f_cm, f_ctm, ...).

• Cross-Section Verification in ULS

The verification of the ultimate limit state in the relevant cross-sections, however, must be conducted using the design values (f_cd, f_yd, ...) of the material properties.

Subject of the Analysis

The column to be examined was modeled based on the evaluation example 0033-D-DBV-AK from [1] and is based on example 10 from [2]. It is located at the edge of a three-span frame structure, consisting of four cantilever columns and three individual beams that are pinned to them.

For the verification, the column is modeled as a single column. It is subjected to the vertical force of the precast beam as well as snow and wind.

System Sketch | Center of Single Column

Nonlinear Stability Verification in RFEM 6

Based on the fundamentals, the nonlinear analysis and verification in the ultimate limit state for the example mentioned above is now carried out.

The Concrete Design and Nonlinear Material Behavior add-ons are required for this purpose.

Materials

Concrete of class C30/37 and reinforcing steel of class B500S(B) are initially selected from the material library.

Concrete

For the material type "Concrete," the nonlinear material model "Anisotropic | Damage" is very well suited for design using the general method.

Stress-Strain Diagram In the material model-specific register "Anisotropic | Damage," various types of diagram definitions can be selected under the category "General," including "ULS C+T | Design Values according to 5.8.6." For this option, the safety factors, which result from the standard chosen in the basic settings for concrete design, are also indicated below.

In the lower part of the dialog in the category "Strengths," the course of the diagram for both the compressive and tensile areas can be controlled by the strength parameters.

For the nonlinear analysis of the column, the compressive area is represented using the diagram type "Parabola" (according to 3.1.5) with compressive strength f_cm and the tensile area with f_ctm.

There is still the option to activate the consideration of tension stiffening using appropriate concrete curves for the tensile area.

The register "Stress-Strain Diagram" shows the resulting diagram underlying the nonlinear analysis.

The following image contains pictures of the input dialog for concrete of the material type "Anisotropic | Damage."

Material Model Anisotropic | Damage – Image 1/4: Assigning Material Model

Creep In the register "Time-dependent Concrete Parameters," creep can be activated.

Reinforcing Steel

For the material type "Reinforcing Steel," the suitable nonlinear material model "Isotropic | Plastic" should be selected.

Stress-Strain Diagram For reinforcing steel, the diagram type can also be set in the specific register. In this example, the default setting is used.

The following image contains pictures of the input dialog for reinforcing steel of the material type "Isotropic | Plastic."

Material Model Assignment for Reinforcing Steel: Isotropic | Plastic (Members)

Structural System and Loading

The modeled structural system and its loading correspond to the specifications from [1] and are summarized in the following image.

Image 1/2: Structural System

Cross-Section – Extended Time-Dependent Parameters When creep is activated in the material dialog, the "Extended Time-Dependent Concrete Parameters" option is available in the dialog for cross-section definition.

The creep parameters applied for the present example are shown in the image below.

Advanced Creep Properties | Concrete Cross-Section Analysis

Member – Design Properties Design properties are activated for the column in the member dialog. The reinforcement is defined according to the reference solution [1] and is summarized in the following image.

Reinforcement Arrangement in Column

Imperfections

Imperfections are determined according to the specifications from Eurocode 2. For the example to be analyzed, the inclination ("initial sway") results in θ_i = 1/315.

Member Imperfection According to EN 1992-1-1

Mesh Settings

In the settings for generating the FE mesh in the Mesh Settings dialog, the option for member divisions, as highlighted in the following image, should be active for the nonlinear analysis of concrete members.

Nonlinear Analysis | Reinforced Concrete Members Settings

Static Analysis

For the nonlinear analysis according to the General Method in EC 2, 5.8.6, the settings are made as highlighted in the image below.

Nonlinear Analysis | Concrete Imperfection

1 - Analysis Type for Linear Creep

In the present example, creep is represented linearly using a modified stress-strain line (see section Creep Deformation). For this, the analysis type "Static Analysis | Creep and Shrinkage (linear)" should be set.

2 - Creep Load Duration

The definition of load durations for creep takes place in the "Times" section.

3 - Second-Order Theory

In the structural analysis settings, the required second-order theory for load combinations is already preset by default.

4 - Consideration of Imperfection

The imperfection to be considered must be activated for the corresponding combinations. The respective assignment can be made in the imperfection case, in the combination assistant, or in the load combination. Further information is provided in the professional article "Consideration of Member Imperfection" as well as in the RFEM 6 online manual chapter Imperfection Cases.

5 - Activate Reinforcement in Structure Modification

In order for the reinforcement stiffness to already be considered in the finite element analysis, it is required to activate the member reinforcement using a Structure Modification for reinforced concrete, as shown below.

Structure Modification | Influence of Reinforcement

6 - Creep-Inducing Load

The relevant quasi-permanent load combination should be used as the creep-inducing load level. The governing combination is set in the "Creep caused by sustained load from" option.

Settings for Concrete Design

For the concrete design, the relevant design situation, the objects to be designed, and their bearing capacity configurations are assigned.

Further information on the input for concrete design is provided in the section Settings for Concrete Design of the introductory example for concrete design.

ULS Design Situations for Concrete Design

The results of the material and physical nonlinear analysis are directly adopted into the concrete design.

The settings for concrete design can be examined in detail in the RFEM file available for download below the article.

Calculation and Results

With the start of the calculation, the nonlinear analysis is followed by the concrete design. Finally, the results are made available for evaluation.

Static Analysis

The following images show results from the nonlinear analysis according to the General Method in EC 2, 5.8.6.

The course of the design moment and the deformations are obtained as follows.

Nonlinear Analysis Results | Creep Behavior

The next image shows the deformation course dependent on the load factor in the calculation diagram for the leading combination LK103 considering creep for the sustained load level. For comparison, the deformations of LK102 without creep are also shown.

Nonlinear Result Analysis | Calculation Diagram

Concrete Design

The proofs of concrete design in the ultimate limit state, including the stability proof according to the General Method in EC 2, 5.8.6, were provided.

An excerpt from the design results is shown in the next image.

Concrete Design Results | ULS Analysis

Conclusion

In the present technical article, the verification according to the general design method of Eurocode 2, 5.8.6, was provided using the example of a reinforced concrete column.

In summary, the procedure can be divided into the following steps.

• Definition of the material with appropriate material models, stress-strain curves, and activation of creep
• Creating the cross-section and setting creep parameters
• Modeling the structural system including design properties
• Defining the loading with imperfections
• Checking mesh settings
• Setting up the Nonlinear Analysis
  • Analysis type (here: "Static Analysis | Creep and Shrinkage (linear)")
  • Second-Order Theory
  • Load durations for creep
  • Activating reinforcement
• Starting the analysis and design
• Result evaluation