V našem příspěvku nejdříve představíme nejčastější typy přípojů s deskou na stojině a uvedeme a částečně vysvětlíme jejich výhody a nevýhody. Přípoji nosníku na sloup se již nebudeme dále zabývat, i když jsou v zásadě možné. Kromě toho bychom neměli opominout ani realizačně technické otázky. Bohužel se v praxi při návrhu spojů v ocelových konstrukcích stále znovu stává, že se vůbec nebo jen nedostatečně vezme v úvahu proveditelnost spoje. Proto se budeme věnovat i těmto případným problémům.
V druhé části našeho příspěvku si ukážeme a vysvětlíme výpočet spojů s deskou na stojině podle EN 1993-1-8 [1] na příkladu spočítaném v modulu RF-/JOINTS Steel-Pinned. Zaměříme se přitom na některá posouzení, která se tu a tam v praxi opomíjejí. Existují pro to různé důvody, z nichž dva nejčastější jsou pravděpodobně tyto: Výpočet by neměl být příliš náročný, neboť se koneckonců jedná „jen“ o přípoj vedlejšího nosníku. Statik není obeznámen s nutností provést to či ono posouzení.
V následujícím příspěvku chceme objasnit, která posouzení je nezbytné provést. V případě škody totiž nepochodíme se zdánlivým argumentem „Dříve to fungovalo i bez tohoto posouzení!“ V průběhu posouzení vychází velmi brzy najevo, jak náročné je posoudit kloubový spoj s deskou na stojině a jak užitečný může být program jako RF-/JOINTS Steel - Pinned, pokud chceme posouzení provést hospodárně a v souladu s normou v rozumném čase.
V poslední části našeho článku si ukážeme, jak velkou nevýhodu přípoje s deskou na stojině a také jiné kloubové spoje mají: Jedná se často o značné zmenšení kritického momentu při klopení. Většinu kloubových spojů a zvlášť pak přípoje s deskou na stojině totiž nelze uvažovat jako vidlicové uložení, což může u potenciálně nestabilních nosníků vést ke značnému snížení jejich únosnosti.
Uspořádání spojů s deskou na stojině
V této části si představíme nejčastější typy spojů s deskou na stojině v provedení nosníku na nosník a zvážíme jejich výhody a nevýhody při výpočtu a posouzení a také při jejich výrobě a montáži. Neusilujeme přitom o vyčerpávající výklad, předkládáme pouze určité poznámky a podněty.
Spoj s deskou na stojině lze v podstatě navrhnout jako přípoj nosníku na sloup anebo také jako přípoj nosníku na nosník. První možností se nebudeme blíže zabývat. U přípojů nosníku na sloup jsou ve většině případů vhodnějším řešením jiné typy kloubového připojení.
Zásadním problémem při montáži spojů s deskou na stojině je, že nelze cíleně vyrovnat výrobní tolerance například v délce nosníku tak, jak je to možné u kloubových spojů s čelní deskou nebo dvojitými úhelníky. Nosníky se tu přitom úmyslně vyrábějí se zkrácenou délkou, která odpovídá maximální toleranci dané normou. Toto zkrácení lze pak na místě stavby vyrovnat dodanými vložkami.
U spojů s deskou na stojině nelze tento postup uplatnit, a proto by se neměly používat mezi dvěma sloupy. Může se pak totiž stát, že nosník lze vsadit pouze silou. Pokud odhlédneme od potíží, které takové vsazení představuje pro montéry, vnášíme do nosné konstrukce navíc také zatížení od vynucených přetvoření, kterých bychom se měli ve skutečnosti vyvarovat.
Velkou výhodou spojů s deskou na stojině obecně je, že není zapotřebí tolik drobných součástí jako u většiny ostatních kloubových spojů. Až na šrouby nejsou potřeba žádné další malé součásti.
Nyní představíme oba nejčastější typy přípojů nosníku na nosník s deskou na stojině. Lze přitom hovořit o spoji s „dlouhou“ anebo s „krátkou“ deskou na stojině.
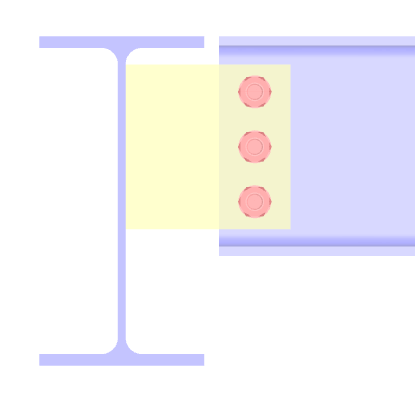
Přípoj nosníku na nosník s „dlouhou“ deskou na stojině:
Spoje s „dlouhou“ deskou na stojině se vyznačují tím, že v připojeném nosníku nejsou zapotřebí žádné výřezy. Deska na stojině je pak dlouhá. Dvě největší výhody tohoto typu spoje tak představují menší nároky kladené na výrobu vzhledem k tomu, že není potřeba složitě zhotovovat výřezy, a dále bezproblémová montáž jednotlivých nosníků.
Výraznou nevýhodou tohoto typu připojení je, že se často velmi vzdálíme od vidlicového uložení. Pokud tedy má být u nosníku možné klopení, pak je bezpodmínečně nutné zohlednit při posouzení nosníku menší tuhost přípoje v kroucení. Vzhledem k tomu, že statický posudek ocelové konstrukce často zpracovává někdo jiný než ten, kdo posuzuje spoje, mohou se vyskytnout problémy.
Protože u tohoto typu přípoje bývá deska také přivařena na jedné nebo na obou pásnicích hlavního nosníku, vzniká téměř bariéra. U žárově pozinkovaných konstrukcí jsou pak zapotřebí přídavné otvory v desce, aby mohl tekutý zinek po vynoření ze zinkové lázně odtékat. Často přitom závisí na smlouvě, zda tyto otvory musí konstruktér zahrnout již do plánování. Ve statickém výpočtu, respektive posouzení lze tyto přídavné otvory zpravidla zanedbat.
Velká excentricita u tohoto typu přípoje si ovšem okamžitě vyžádá větší tloušťku plechu desky. Což ovšem opět vede k tomu, že je potřeba značně zesílit svary, protože k zajištění duktility dílce musí mít svary větší únosnost než připojený plech. Přitom nesmíme zapomínat na to, že koutové svary s kořenem 6 mm a větším je třeba provařit v několika vrstvách. Přípoj se tak rychle stává z materiálově technického a výrobního hlediska nehospodárný.
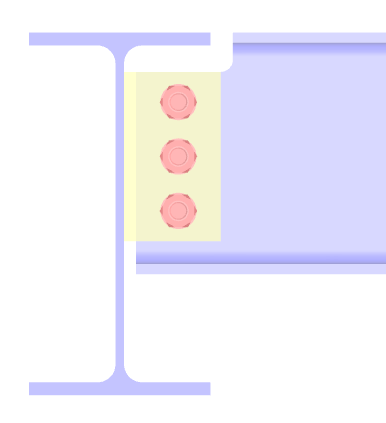
Přípoj nosníku na nosník s „krátkou“ deskou na stojině:
Toto uspořádání přípoje vykazuje veškeré výhody varianty s „dlouhou“ deskou na stojině až na bezproblémovou montáž jednotlivých nosníků. V případě menších vzdáleností mezi nosníky se může stát, že jednotlivý nosník nelze na místě stavby vmontovat.
Protože se ale pracovní plošiny a lávky často předem smontují na zemi a následně se osazují na místě stavby vcelku anebo po velkých konstrukčních částech, bývají se vsazením jednotlivých nosníků zřídkakdy problémy. Pokud je to možné, měl by se projektant anebo také konstruktér každopádně s montážní technologií prováděcí firmy dobře obeznámit.
Další předností spoje s „krátkou“ deskou na stojině je zpravidla mnohem menší excentricita přípoje, což často vede k hospodárnějším výsledkům než u spoje s „dlouhou“ deskou.
Naopak nevýhodou tohoto spoje je zpravidla nutnost provést výřez u vedlejšího nosníku, což s sebou také v určitých případech přináší tři problémy. V první řadě se jedná o náročnější výrobu, která však již v moderních výrobních halách téměř nestojí za zmínku.
Druhý problém spočívá v nižší únosnosti nosníku v oblasti výřezu, což vyžaduje další zvláštní posouzení, která mnohdy také mohou být rozhodující. Zejména se jedná o případ, kdy je zapotřebí výřez na obou stranách, tedy na horní i dolní pásnici nosníku. Taková situace nastává, pokud jsou vedlejší i hlavní nosník přibližně stejně vysoké.
Třetí problém, který z výřezu může vyplynout, se týká pouze žárově pozinkovaných konstrukcí z vysokopevnostní oceli (od S355). V tomto případě je třeba posoudit, zda při žárovém zinkování nedochází k tvorbě trhlin v oblasti výřezu. Provést lze podle směrnice 022 německého výboru pro ocelové konstrukce (DASt-Richtlinie 022) buď statický výpočet anebo klasifikaci detailu, přičemž klasifikaci lze označit za standardní postup.
Příklad posouzení krátkého spoje s deskou na stojině s výřezem
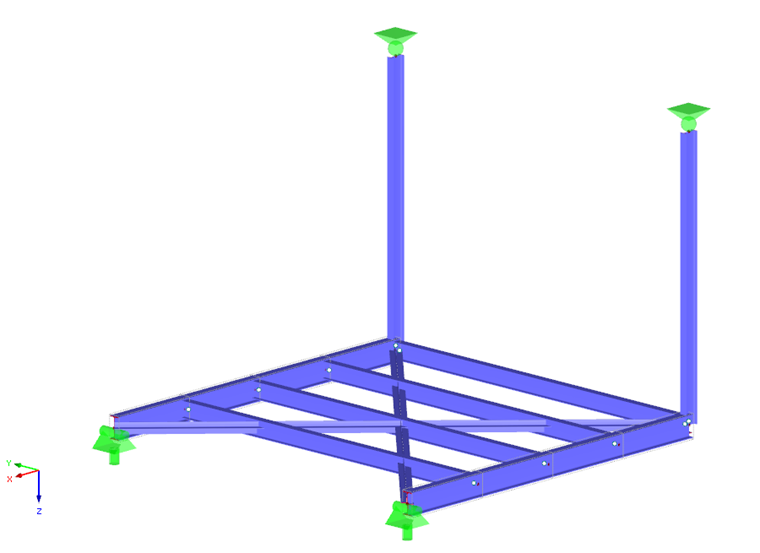
V této části si ukážeme a do jisté míry vysvětlíme výpočet spoje s deskou na stojině podle EN 1993-1-8 [1]. Na obr. 03 je znázorněna příslušná pracovní plošina. Její půdorys má rozměry 4,00 m x 4,00 m. Na jedné straně je zavěšena na hlavní plošinu, která se nachází nad ní, a na druhé straně je připojena k hlavní konstrukci. Plošinu tak lze vzhledem k jejímu uložení „vyjmout“ z globálního výpočtu. Není to sice nezbytně nutné, výpočet a posouzení jsou ale pak většinou přehlednější a někdy i rychlejší.
Po (předběžném) posouzení v přídavném modulu RF-/STEEL EC3 byl pro hlavní nosník zvolen průřez IPE220-S235JR a pro plošinový nosník průřez IPE180-S235JR. Pro závěsy byl z konstrukčních důvodů navržen profil IPE160-S235JR. Vyztužení plošiny se tu dále nemá uvažovat.
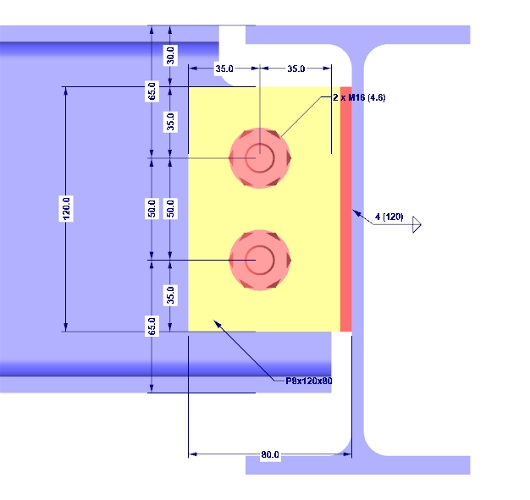
Na obr.04 můžeme vidět spoj s deskou na stojině a jeho nejdůležitější rozměry. Další rozměry případně uvedeme v průběhu posouzení. Vnitřní síly ve spoji činí:
Ještě než provedeme jednotlivé kroky posouzení a částečně je vysvětlíme, tak musíme zmínit, že základním předpokladem samozřejmě je, aby výška styčníkové desky byla menší než výška stojiny vedlejšího nosníku. Má se tak zabránit kontaktu mezi připojeným nosníkem a podpůrnými konstrukčními prvky. S tímto záměrem se také provádí první část posouzení, na kterou se nyní podíváme.
Dovolené pootočení v kloubovém spoji:
Toto posouzení patří k těm, kterou statici v praxi rádi opomíjejí, přitom lze díky tomuto posouzení bezpečně uvažovat kloubový spoj tam, kde se uvažoval při výpočtu vnitřních sil. Při tomto posouzení se střed otáčení uvažuje v geometrickém těžišti sestavy šroubů. Vypočítá se přitom úhel, od kterého dochází ke kontaktu mezi pásnicí nosníku a podpůrným dílcem (zde stojinou hlavního nosníku).
Kontakt je v podstatě možný.
Spoj připouští návrhová pootočení 0,45°, posouzení je splněno.
Zabránění předčasnému porušení svarů:
Posouzení svarů se v zásadě provádí podle článku 4 normy EN 1993-1-8 [1]. Při relativně malých zatíženích v porovnání s únosností připojeného nosníku ve smyku mohou mít nutné svary velmi malou tloušťku. V takovém případě je často únosnost svarů menší než únosnost jiných komponent. Případné selhání přípoje se pak vyznačuje křehkým porušením svaru. Přípoj nemá téměř žádnou duktilitu.
Pro svar jsme zvolili tloušťku 4 mm. Kritérium je tak splněno.
Porušení jednotlivých šroubů střihem:
Obtížné u tohoto posouzení je pouze správně rozdělit vnitřní síly ve spoji na jednotlivé šrouby. Obecně popisuje rozdělení sil mnoho příruček, proto se jím na tomto místě nebudeme podrobněji zabývat.
Křehké porušení skupiny šroubů střihem:
Podmínka posouzení má v tomto případě zaručit možnost plastického přerozdělení vnitřních sil ze skutečného stavu do návrhového stavu. Toto kritérium by kromě toho nemělo být nikdy rozhodující, to znamená, že při tomto posouzení by nikdy nemělo být dosaženo maximální využití.
Únosnost otvoru pro šroub v otlačení ve styčníkové desce:
Vzhledem k tomu, že spoj s deskou na stojině má vždy jednu střihovou plochu, odpovídají složky sil silám při porušení ve střihu. Další výpočet tak není třeba.
Porušení smykem v neoslabeném průřezu styčníkové desky:
Porušení smykem v oslabeném průřezu styčníkové desky:
Vytržení skupiny šroubů v desce:
Návrh na vytržení skupiny šroubů představuje stejně jako posouzení na střih a otlačení jednotlivých šroubů standardní posouzení. Podrobněji se jím nyní nebudeme zabývat. Přesnější popis vzorců pro posouzení najdeme v různých příručkách.
Porušení desky ohybem:
Tento mechanismus porušení v mnoha případech odpadá. Protože však výpočet únosnosti desky v ohybu opravdu není náročný, většinou se hodnota únosnosti vypočítá. Lze však vyloučit, že tento mechanismus selhání může být rozhodující, pokud výška desky na stojině přesahuje rameno ramene z 2,73. V tomto případě je únosnost v ohybu vždy vyšší než smyková únosnost v neoslabeném průřezu desky.
Boulení desky:
Toto posouzení se v praxi často opomíjí. Při nevýhodných geometrických podmínkách může přitom jít právě o rozhodující posouzení. Toto posouzení vychází ze starého britského předpisu BS 5950-1 [3] z roku 2000. Pro přesnější popis tak odkazujeme na tuto směrnici a také na komentáře k ní.
Únosnost při boulení, respektive únosnost při klopení tedy závisí na pevnosti desky ve vzpěru, která se zas odvíjí od štíhlosti desky. Hodnotu pevnosti lze převzít z britské normy BS 5950-1 [3] v tabulce 17, přičemž je třeba zmínit, že ve Velké Británii se konstrukční oceli o pevnosti S235 nepoužívají nebo používají jen zřídka; proto pro tuto ocel nejsou výslovně uvedeny žádné hodnoty. Lze ovšem použít hodnoty pro ocel S275 a mez kluzu pro S235.
Teoreticky by tak byl návrh na boulení možný, postrádá ovšem smysl. Zdá se, že lepší je tento způsob porušení styčníkové desky zcela vyloučit. Je třeba k tomu splnit následující posouzení.
Porušení styčníkové desky tahem v neoslabeném průřezu:
Toto posouzení je nutné, pouze pokud působí v přípoji normálové síly. Ačkoli je namáhání normálovou silou malé a lze ho označit za zanedbatelné, příslušné posouzení pro úplnost uvedeme.
Porušení stojiny nosníku tahem v oslabeném průřezu:
Posouzení pevnosti nosníku v oblasti výřezu:
Toto posouzení je často rozhodující, pokud je nutné zhotovit výřezy na obou stranách nosníku. Přitom je třeba prokázat, že působící ohybové momenty a posouvající síly lze také bezpečně přenášet v oblasti výřezu.
Posouvající sílu lze při dalším posouzení zanedbat. Teoreticky by bylo možné provést také posouzení srovnávacího napětí, od kterého ovšem upustíme. Pouze spočítáme a vyhodnotíme normálové napětí od ohybových momentů a normálových sil.
Únosnost otvoru pro šroub v otlačení ve stojině nosníku:
Působící síly odpovídají silám v desce. Hodnoty únosnosti je ovšem třeba vzhledem k rozdílným tloušťkám plechu znovu spočítat.
Porušení smykem v neoslabeném průřezu stojiny nosníku:
Porušení smykem v oslabeném průřezu stojiny nosníku:
Vytržení skupiny šroubů ve stojině nosníku:
Porušení stojiny nosníku tahem v neoslabeném průřezu:
Toto posouzení je nutné, pouze pokud působí v přípoji normálové síly. Ačkoli je namáhání normálovou silou malé a lze ho označit za zanedbatelné, příslušné posouzení pro úplnost uvedeme.
Porušení stojiny nosníku tahem v oslabeném průřezu:
Porušení stojiny hlavního nosníku ohybem:
Toto posouzení je nezbytné u jednostranných anebo oboustranných, ale nestejně zatížených přípojů na stojinu sloupu. Toto posouzení je třeba provést i v případě, že je deska přivařena pouze na stojinu nosníku. Jistě se nejedná o běžný případ, protože v praxi se deska obvykle přivaří ještě na pásnici hlavního nosníku. V našem příkladu jsme ovšem toto uspořádání spoje zvolili úmyslně, abychom v krátkosti předvedli i toto posouzení.
Vzhledem k malým normálovým silám by se v praxi neprovádělo ani toto posouzení, protože porušení stojiny hlavního nosníku lze předem vyloučit.
Nyní jsme posouzení přípoje úspěšně dokončili. Veškeré podmínky posouzení byly splněny.
Na tomto místě je ještě třeba podotknout, že při posouzení jsme uvažovali pouze jednu kombinaci zatížení. Teoreticky by bylo třeba provést posouzení jednotlivě pro všechny potenciální návrhové kombinace, čímž by se ovšem posouzení značně rozšířilo. V praxi se přitom často postupuje tak, že se použijí vnitřní síly z obálky hodnot, což ovšem v nejhorším případě může vést k velmi nehospodárným přípojům.
Vliv typu spoje na stabilitu konstrukčního prvku
Nakonec je třeba zmínit největší problém spojů s deskou na stojině a s jinými typy kloubových spojů: Jedná se o značný odklon od vidlicového uložení. Při tomto odklonu většinou nejsme na rozdíl od ohybově tuhých spojů na straně bezpečnosti, což je z bezpečnostně-technického hlediska důležitý fakt.
Našim cílem teď není ukázat jedinou správnou cestu, nýbrž jak se statik může s tímto problémem vypořádat.
U ocelových konstrukcí se často stává, že osoba odpovědná za návrh nosníků neposuzuje všechny spoje v konstrukci. Zpravidla navrhne patky sloupů a hlavní spoje konstrukce a vedlejší přípoje přenechá prováděcí firmě. Projektanti a konstruktéři z prováděcí firmy beztak vědí nejlépe, jaké spoje jsou vhodné při používané výrobní a montážní technologii.
Velkým problémem při daném postupu práce je, že statik odpovědný za návrh nosníků se sotva zaobírá tím, zda přípoje vedlejších nosníků také odpovídají jeho předpokladům. U plošinových nosníků náchylných ke klopení bude běžně vycházet z vidlicového uložení na koncích nosníku, což ovšem statikovi posuzujícímu přípoje může někdy působit problémy. Otázka tak zní, co lze učinit již při návrhu nosníků, aby byla snazší práce s následným návrhem přípojů.
Stará německá norma DIN 18800-2 platná pro ocelové konstrukce ještě nabízela možnost zohlednit výřezy v nosníku při posouzení na klopení tak, že nosníku s výřezem se přiřadil součinitel n = 2,0 (na rozdíl od součinitele pro nosníky bez výřezu n = 2,5). Tomu by při posouzení podle aktuálního Eurokódu odpovídalo přiřazení o jeden stupeň nepříznivější křivky klopení, například křivky c místo křivky b. Takové zohlednění zářezu není v EN 1993-1-1 [2] stanoveno. U kloubově připojených vedlejších nosníků v ocelové konstrukci by se měla křivka klopení vždy překlasifikovat, aby osoba pověřená návrhem přípojů nemusela v daném bodě nutně vytvářet vidlicové uložení. Alternativu k překlasifikování křivky klopení by představovalo omezení míry vytížení vedlejších nosníků při klopení určitou hodnotou (například 80 %).
Při posouzení přípojů je beztak nezbytné navrhnout vedlejší nosník na menší tuhost spoje, což lze ovšem pouze v případě, že nám byla ponechána určitá rezerva v původním návrhu. O tom, jak má dané posouzení vypadat, pak rozhoduje sám statik. O normy se bohužel v tomto případě nelze opřít.
Menší tuhost spoje při posouzení nosníku lze uvažovat v podstatě dvěma způsoby: Buď ji zohledníme přímo v podepření zadáním torzní pružiny anebo použijeme tabulkové hodnoty či diagramy pro výpočet ideálního kritického momentu vzpěru.
Doporučit lze přitom druhé řešení, pokud se má ručně provést posouzení metodou náhradního prutu. Protože není naším úmyslem zabývat se v tomto příspěvku konkrétně tímto posouzením, odkážeme pouze na užitečnou literaturu. Velmi doporučujeme články [5] , [6] a [7]. Bohužel dosud nebyla zveřejněna příslušná výzkumná zpráva DASt k [6] a [7] , což by mohl být v této oblasti nejužitečnější zdroj v němčině.
Možnost zohlednit vhodnou torzní pružinu je jistě řešením, pokud se má posouzení provést obecnou metodou podle čl. 6.3.4 normy EN 1993-1-1 [2] nebo výpočtem podle druhého řádu klopení teorie. Při výpočtu můžeme uplatnit metodu konečných prvků, a využít přitom lze například program RFEM.