Description
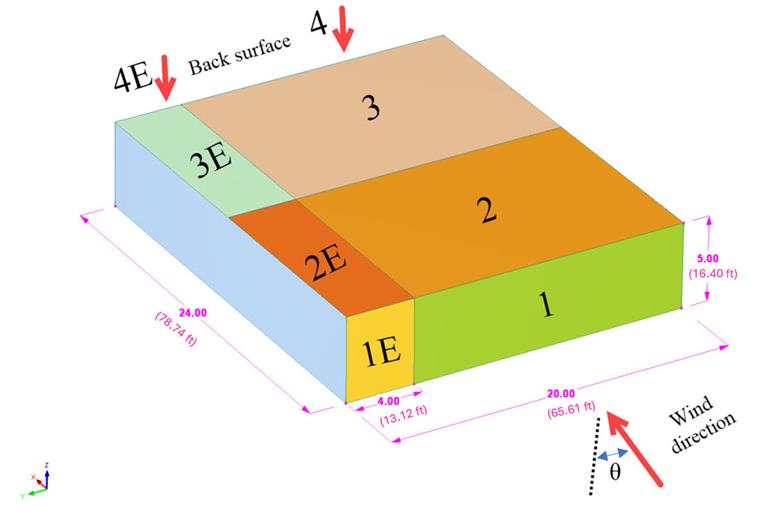
In the current validation example, we investigate the wind pressure coefficient (Cp) of the flat roof and walls with ASCE 7-22 as minimum design loads and associated criteria for buildings and other structures [1]. In section 28.3 (Wind loads - main wind force resisting system) and Figure 28.3-1 (load case 1), there is a table that shows the Cp value for different roof angles. In the current example, we selected θ=0 as a flat roof.
Although computational fluid dynamics (CFD) simulations are being utilized more often in wind engineering applications, ASCE 49 does not clearly describe all of the essential techniques for CFD. Any use of CFD to determine the design main wind force resisting system (MWFRS), C&C, or other structures' wind loads requires peer review as well as a verification and validation (V&V) study [2]. This is because a similar standard is still needed to document the procedures required to obtain reliable and accurate wind loads using CFD tools. In the meantime, this standard will be developed. To address quality assurance and quality control of this procedure in the absence of a standard, this is required [1].
Finding the most compatible configurations with standards regarding input data, such as turbulence models, wind velocity profiles, turbulence intensities, boundary layer conditions, order of discretization, and other factors, is the key factor of CFD simulation. The important point is the standards do not cover the required information for numerical simulation, such as CFD simulation. In the current VE, we presented the most compatible RWIND settings in relation to the example of the ASCE 7-22 roof and walls.
Analytical Solution and Results
The three-dimensional enclosed model (unit: m (ft)) is assumed according to Figure 1 which illustrate 8 wind zones (1,2,3,4,1E,2E,3E,4E). The external pressure coefficients (GCpf ), for enclosed, partially enclosed, and partially open buildings with low-rise walls and roofs is presented in Figure 28.3-1 of ASCE 7-22. The important assumptions and input data are also shown in Table 1.
| Table 1: Dimensional Ratio and Input Data | |||
| Basic Wind Velocity | V | 30 (67.10) | m/s (mph) |
| Terrain Category | 2 | - | - |
| Mean Roof Height | h | 5 (16.40) | m (ft) |
| Horizontal Dimension (Edge Distance) | α | 4 (13.12) | m (ft) |
| Roof Angle | θroof | 0 | Degree |
| Air Density - RWIND | ρ | 1.25 (0.078) | kg/m3 (lb/ft3) |
| Wind Directions | θwind | 0, 22.5, 45 | Degree |
| Turbulence Model - RWIND | Steady RANS k-ω SST | - | - |
| Kinematic Viscosity (Equation 7.15, EN 1991-1-4) - RWIND | ν | 1.5*10-5 (1.6*10-4) | m2/s (ft2/s) |
| Scheme Order - RWIND | Second | - | - |
| Residual Target Value - RWIND | 10-4 | - | - |
| Residual Type - RWIND | Pressure | - | - |
| Minimum Number of Iterations - RWIND | 800 | - | - |
| Boundary Layer - RWIND | NL | 10 | - |
| Type of Wall Function - RWIND | Enhanced / Blended | - | - |
| Turbulence Intensity (Best Fit) - RWIND | I | Terrain 2 | - |
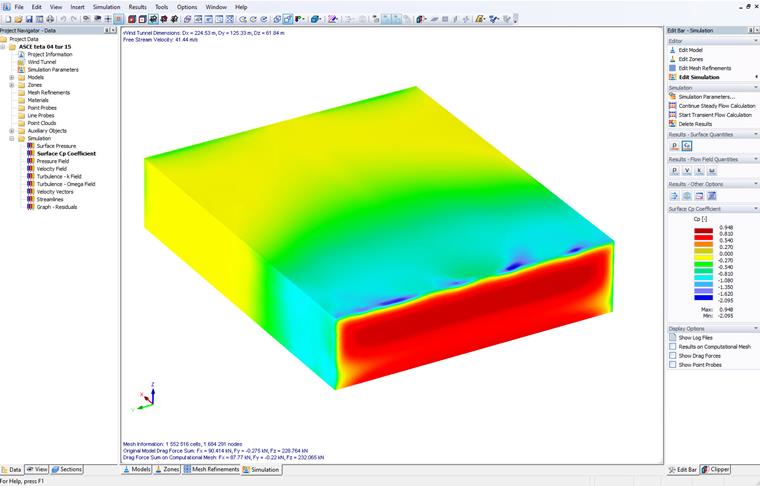
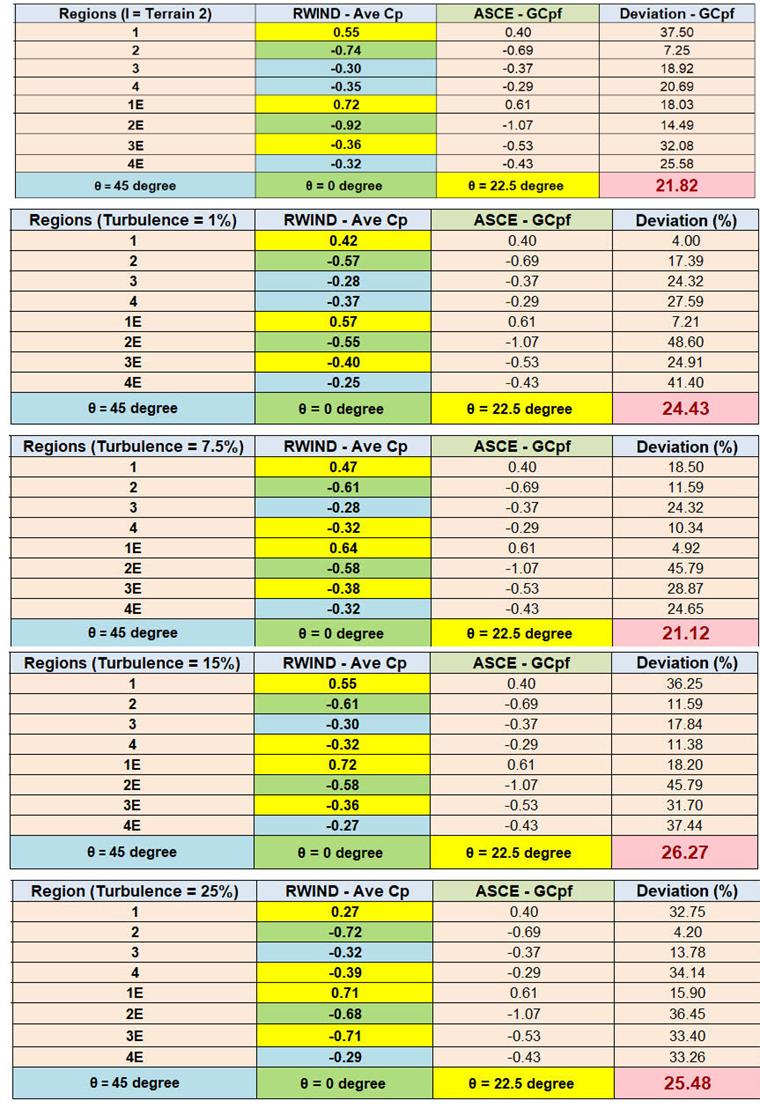
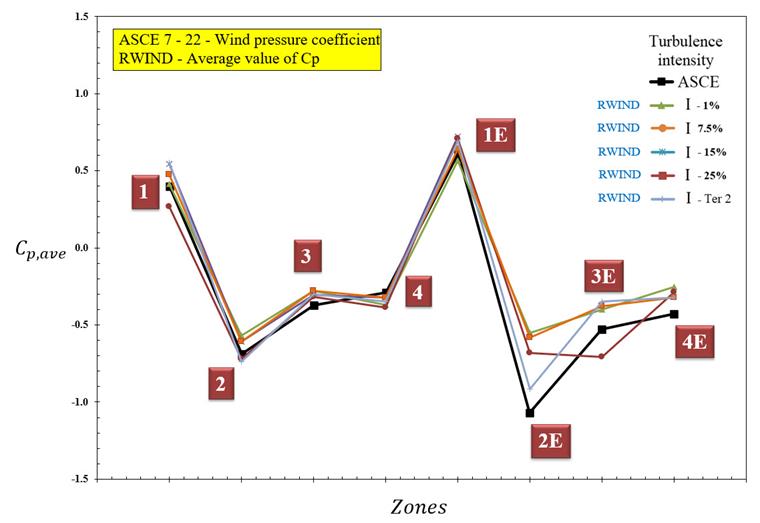
The average wind pressure coefficient Cp is calculated for various zones with different turbulence intensities. Three wind directions (θ= 0, 22.5, 45 degrees) are considered to find the critical value of Cp. The Cp contour is illustrated in Figure 2. The table of the deviation values and the diagram of the Cp value under different turbulence intensities are shown in Figure 3 and Figure 4. Four constants and one variable (based on terrain 2) of turbulence intensity are considered for performing wind simulations. The results show a good agreement when the turbulence profile is close to the Terrain 2 category.
Conclusion
In the current example, we investigated the validation of average roofs and walls Cp value, which was presented in ASCE 7-22 using RWIND. The results show that recommended RWIND configuration has good agreement with the standard. The higher turbulence intensity close to the variant turbulence profile of Terrain 2 shows more accurate results rather than the low turbulence profile. It is important to consider the critical wind direction Scenario to obtain an extreme value of ASCE 7-22. The deviation values (around 20% differences) mostly came from safety factors and the statistical approach used in standards.
Also, the flat roof model with recommended settings is available to download here: