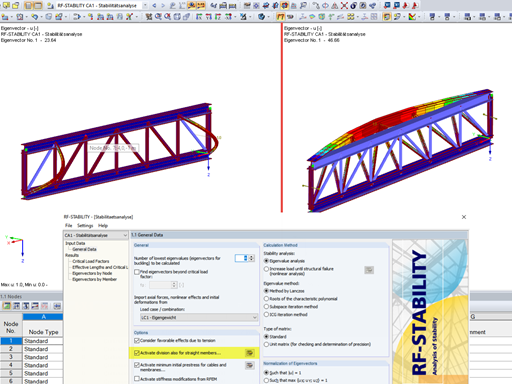
RSBUCK uses a momentary representation of the axial force distribution in the respective load state. The axial forces are increased iteratively until the critical load case occurs. In the numerical analysis, the stability load is indicated by the fact that the determinant of the stiffness matrix becomes zero.
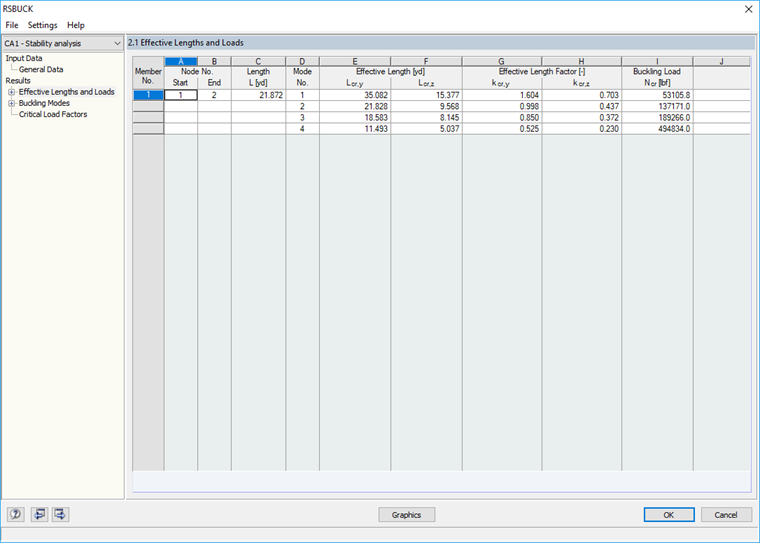
If the effective length factor is known, the buckling load and buckling mode are determined based on this. For the lowest buckling load, all effective lengths and effective length factors are determined.
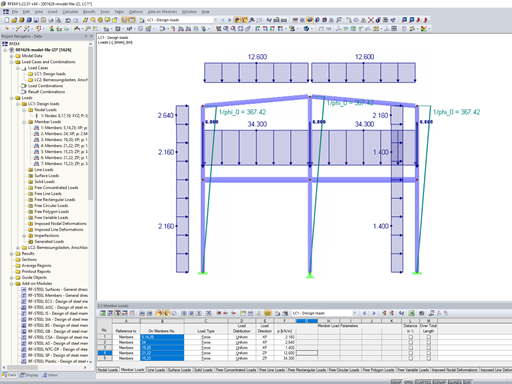
Example: A hinged column with a length of 20 m, cross-section HE‑B 500, self-weight load
For the first buckling mode, you obtain the effective length factor of kcr,y = 2.92 for the buckling about the major axis. For the buckling about the minor axis with a buckling load of 651.3 kN, you obtain an effective length factor of 1.00.
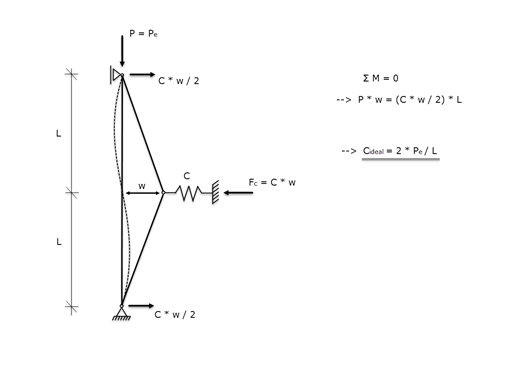
If you set the expression for determining the buckling load Ncr = π² * E * I / Lcr² to Lcr and apply Ncr = 651.3 kN and Iy = 107,200 cm4, you obtain the Lcr,y of 58.4 m, which results in the effective length factor kcr,y of 2.92.
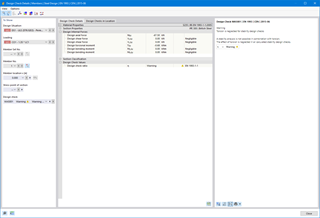
In RSBUCK, two effective length factors are determined for each buckling mode and buckling load.
In order to obtain the correct effective length factor for the deflection perpendicular to the y-axis (buckling about the major axis), it is necessary to calculate several buckling modes (mode shapes). The correct value is displayed in Window 2.1. In the example, it is the third buckling mode with a buckling load of 5,485.5 kN. For this load, the effective lengths and effective length factors are determined as follows: kcr,y = 1.0 and kcr,z = 0.345.
In the case of a quadratic cross-section, two equal effective lengths result, as the stiffnesses in both directions are the same.