The shear area is calculated as follows:
|
Iz |
Second moment of area in relation to the axis z or y |
|
Sz |
First moment of area in relation to the axis z |
|
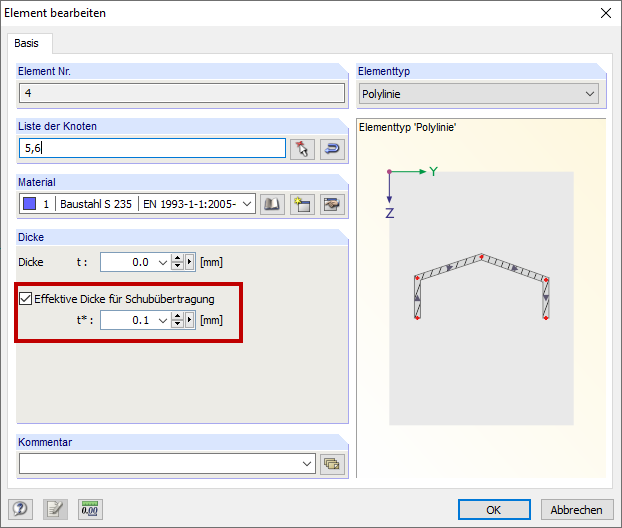
t* |
Effective element thickness for the shear transfer |
|
A* |
Surface area based on the effective shear thickness t* |
|
Iy |
Second moment of area in relation to the axis y |
|
Sy |
First moment of area related to the axis y |
|
t* |
Effective element thickness for the shear transfer |
|
A* |
Surface area based on the effective shear thickness t* |
The effective element thickness for the shear transfer t* has a significant influence on the shear area. Therefore, the defined effective element thickness for the shear transfer t* (Image 01) of the elements should be checked.