General
The limit values for the appearing deformation of reinforced concrete components are predefined by the uncracked and cracked cross-section conditions. RF-CONCRETE Deflect offers deformation analysis taking into account the cracked state in the cross-section. The effective stiffnesses in the finite elements according to the existing cross-section condition are calculated. These effective stiffnesses are used for the surface elements in a subsequent FEM calculation. The effective stiffnesses are controlled by the distribution coefficient ζ, which will be explained further in the following text.
Applying the Deformation Coefficient ζ in the Deformation Analysis
The deformation coefficient ζ is also called cracking or damage factor in literature. Use of the deformation coefficient ζ in the deformation analysis is specified in Equation 7.18 of EN 1992-1-1 [1].
The variable a represents the analyzed deflection parameter (for example, curvature). aI and aII are the deformation parameters for the uncracked and cracked states. The equation shows that ζ = 0 will govern for the uncracked cross-section state (state I).
If you use the general deflection parameter a for the cross-section curvature
, you will receive an approach to determine the effective cross-section stiffness.
Determining the Distribution Coefficient ζ
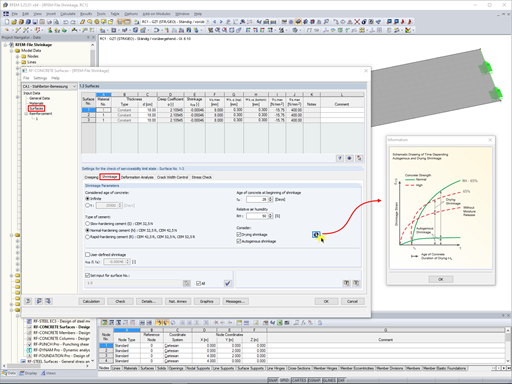
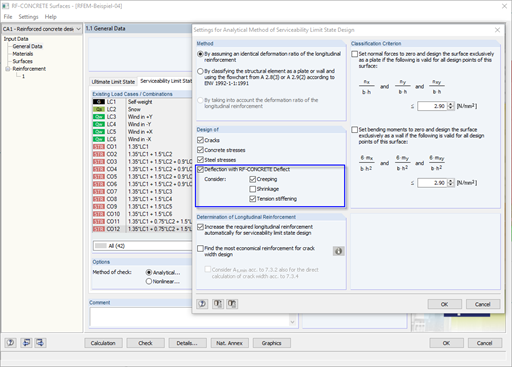
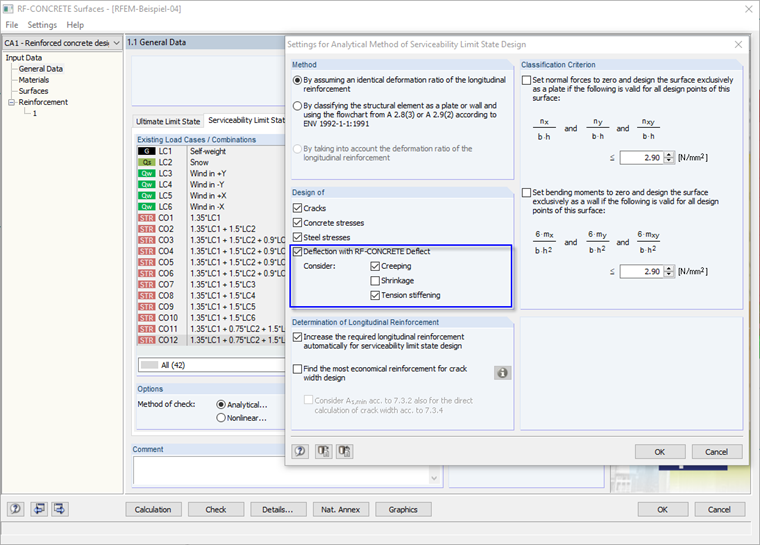
The distribution coefficient ζ is an indicator in the deformation analysis that shows whether a cross-section is uncracked or cracked. In addition, the factor ζ considers the interaction of the concrete between the cracks (tension stiffening). Applying tension stiffening can be controlled in the settings of RF-CONCRETE Deflect (see Figure 01). Therefore, these two situations (taking into account and not taking into account the tension stiffening between the cracks) will be examined in the following text.
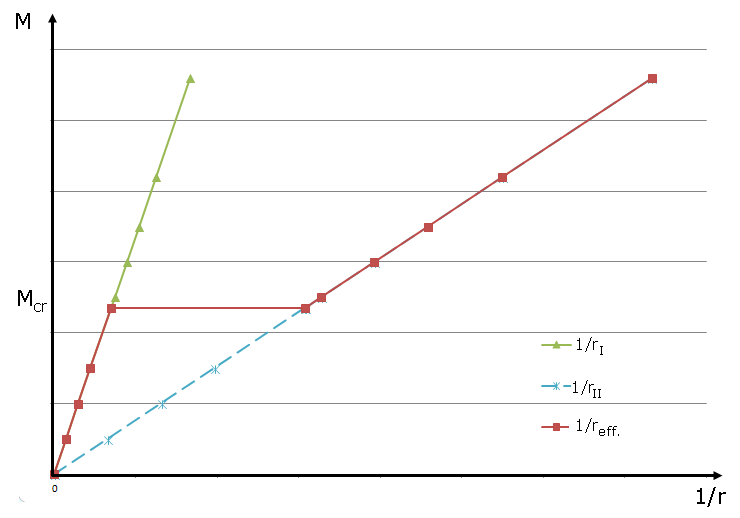
If the interaction of the concrete between the cracks is not applied in the deformation analysis, the distribution coefficient has only two values. ζ equal 0 is set for the uncracked cross-section and equal 1 for the cracked cross-section. This effect is clearly visible in the corresponding moment-curvature diagram. The curvature remains in state I for a loading with crack internal force Mcr. When the crack's internal force is exceeded, the curvature for the fully cracked cross-section will govern.
If the approach for tension stiffening is used in the deformation analysis, the distribution coefficient is in a range between 0 and 1. For loading above the cracking internal forces, the distribution coefficient is determined according to the specifications of the respective design standard. When performing the deformation analysis according to EN 1992-1-1 [1], the factor is calculated as follows in RF-CONCRETE Deflect:
where
β = parameter for the influence of load duration or load repetitions
fctm = mean tensile strength of concrete
σmax = concrete tension stress under the assumption of linear-elastic material behavior
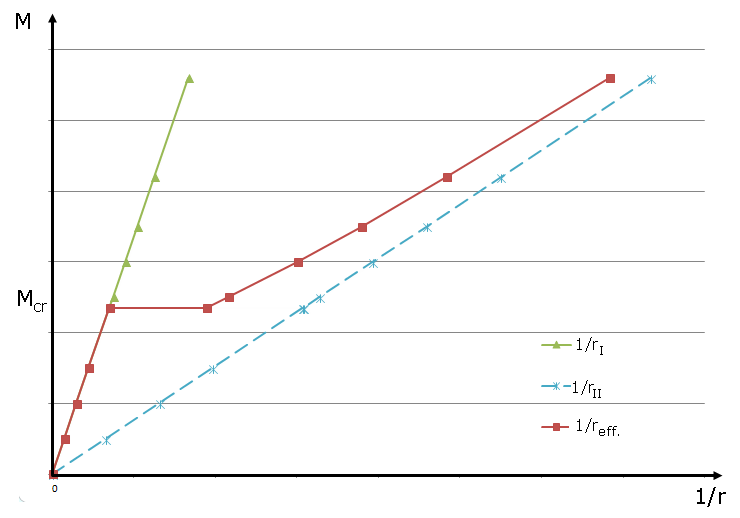
The influence of tension stiffening on the mean deformation or curvature is clearly visible in the moment-curvature diagram of Figure 03. When loaded, the effective curvature is above the crack's internal forces between the uncracked and cracked areas and continuously approaches the cracked state with higher loading.
Summary
The moment-curvature diagrams shown in this article indicate that the approach of tension stiffening has a significant impact on the determination of the distribution value ζ and thus on the mean curvature and the deformation. Depending on the task in question, it is up to the engineer to decide whether or not to apply the load capacities from the contribution of concrete between the cracks when performing deformation analysis. Not considering the tension stiffening effect is a safe approach, as shown in Figure 02, because a completely cracked cross-section state is used for the deformation analysis when the crack's internal forces are exceeded.





















.png?mw=350&hash=5c4b2144aa52cd2928e41d7b311671dea882afa3)