2688x

001857

Dipl.-Ing. (FH) Richard Haase

2024-02-01

Fatigue Design According to EN 1992-1-1 in RFEM

The fatigue design according to EN 1992-1-1 must be performed for the structural components subjected to large stress ranges and/or many load changes. In this case, the design checks for the concrete and the reinforcement are performed separately. There are two alternative design methods available.

Introduction

The fatigue design of reinforced concrete components is based on an explicit fatigue design (Design Level 3). This design has a high accuracy, but as a result, it requires a large amount of computational effort. Therefore, two simplified design methods have been developed to keep the computation time low. There are Design Level 1, which defines the maximum allowable stress range, and Design Level 2, which performs a simplified fatigue design with damage equivalent stresses.

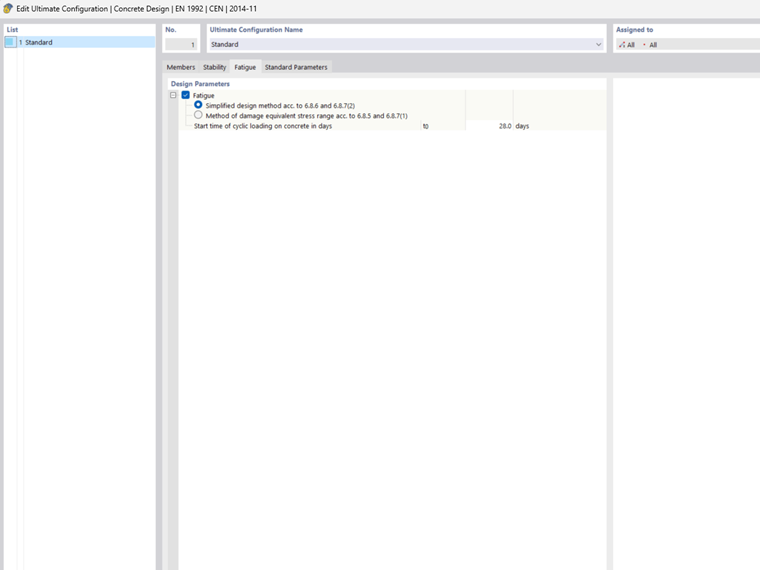
In RFEM 6, Design Level 1 and Design Level 2 are implemented.

Design Level 1 = Simplified Method

Design Level 1 – Ultimate Configuration

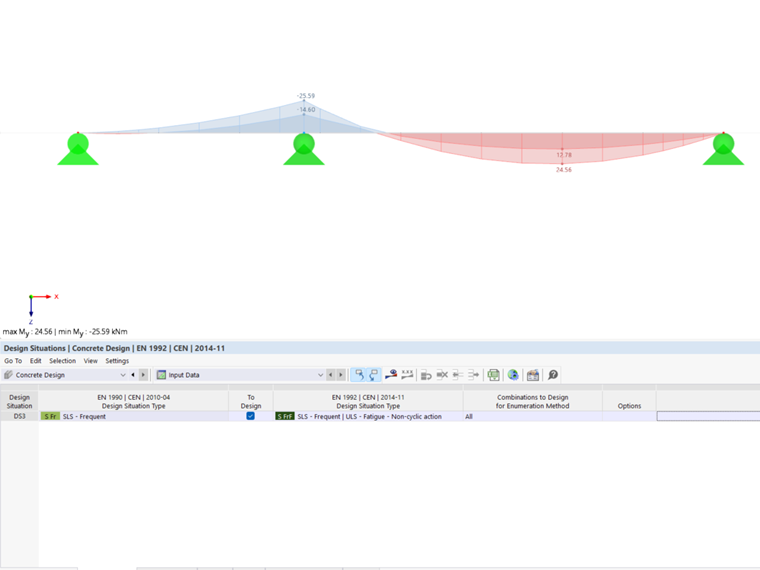
Design Level 1 – Design Setting

For this design, the basic combination of the acyclic actions according to Eq. 6.67, EN 1992‑1‑1 is required. It corresponds to the "SLS – Frequent" action combination in accordance with Eq. 6.15 according to EN 1990).

\sum_{j \geq 1} G_{k, j} " + " P " + " ψ_{1, 1} Q_{k, 1} " + " \sum_{i > 1} ψ_{2, i} Q_{k, i}

Action Combination SLS Frequent

In the case of longitudinal reinforcement design, the maximum steel stress range must not exceed the stress range value specified in the standard. The loads from bending and axial force, as well as an interaction of torsion, bending, axial force, and shear, are each designed. In this case, Δσ_S,max is the maximum steel stress range, and k₁ is the factor for the allowed stress range.

η = \frac{∆ σ_{S, m a x}}{k_{1}}

Longitudinal Reinforcement Design, Simplified Design Method According to 6.8.6

The shear design is performed with and without reinforcement. For the design check without shear reinforcement, it is necessary to meet the following condition.

V_{Ed, \min} / V_{Ed, \max} \geq 0

\frac{|V_{E d, m a x}|}{|V_{R d, c}|} \leq 0.5 + 0.45 \frac{|V_{E d, m i n}|}{|V_{R d, c}|} \{\begin{cases} \leq 0.9 until C 50 / 60 \\ \leq 0.8 as of C 55 / 67 \end{cases}

V_{Ed, \min} / V_{Ed, \max} < 0

|\frac{V_{Ed, \max}}{V_{Rd, c}}| \leq 0.5 - |\frac{V_{Ed, \min}}{V_{Rd, c}}|

Shear Design Without Reinforcement According to 6.8.7 (4)

In the case of a design with shear reinforcement, the shear force stress range must not exceed the stress range specified in the standard.

∆ σ_{S w, m a x} = |V_{E d, m a x} - V_{E d, m i n}| \times \frac{\tan (θ_{f a t})}{a_{s w, V_{E d}} \times d \times 0.9}

η_{S w} = |\frac{∆ σ_{S w, m a x}}{k_{1}}|

Shear Design with Reinforcement, Simplified Design Method According to 6.8.6

The design checks for the concrete compressive stress and the concrete compression struts need to meet the following condition. For the design check of the concrete compression struts, f_cd,fat is reduced by the factor ν₁ for shear cracks. The concrete compressive stresses are determined from the bending and axial forces, and the concrete strut stresses from the shear and torsional forces.

\frac{σ_{c, m a x}}{f_{c d, f a t}} \leq 0.5 + 0.45 \frac{σ_{c, m i n}}{f_{c d, f a t}} \begin{array}{rcl} \leq & 0.9 & for f_{ck} \leq 50 N / mm ² \\ \leq & 0.8 & for f_{ck} \geq 50 N / mm ² \end{array}

Design of Concrete Compressive Stress and Concrete Compression Struts, Simplified Analysis Method According to 6.8.7 (2)

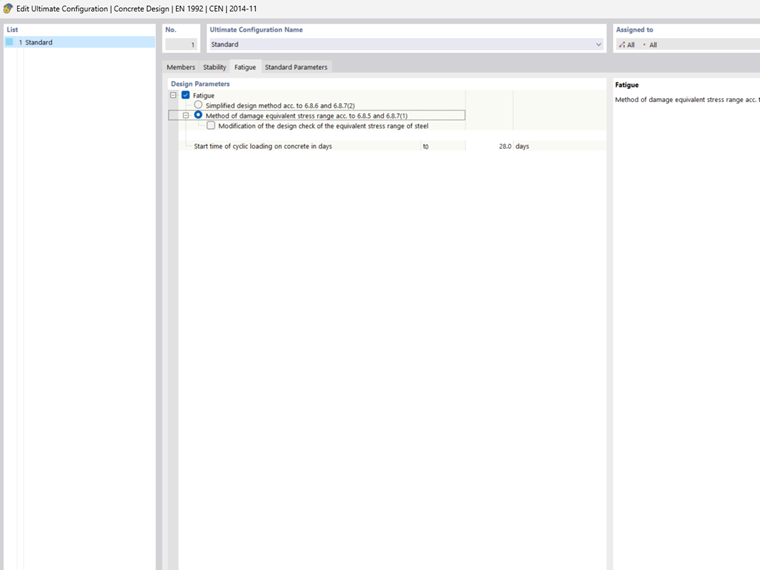
Design Level 2 = Method of Damage Equivalent Stress Range

Design Level 2 – Ultimate Configuration

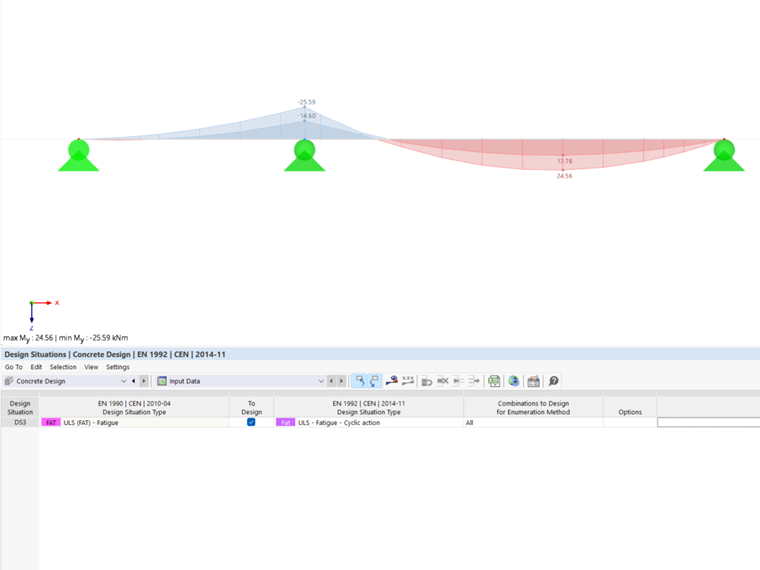
Design Level 2 – Design Setting

For this design check, it is necessary to combine the cyclic action with the unfavorable basic combination according to Eq. 6.69 in EN 1992‑1‑1.

(\sum_{j \geq 1} G_{k, j} " + " P " + " ψ_{1, 1} Q_{k, 1} " + " \sum_{i > 1} ψ_{2, i} Q_{k, i}) " + " Q_{f a t}

Action Combination as per Eq.6.69

The following design check has to be fulfilled for the longitudinal reinforcement. The loads from bending and axial force, as well as an interaction of torsion, bending, axial force, and shear, are each designed.

γ_{F, f a t} \times ∆ σ_{s, e q u} (N *) \leq ∆ σ_{R s k} (N *) / γ_{s, f a t}

Longitudinal Reinforcement Design, Method of Damage Equivalent Stress Range According to 6.8.5 (3)

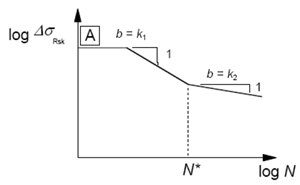
The damage equivalent stress ranges for the N* load cycles must be smaller than the allowable stress ranges for the N* load cycles according to the S-N curves.

Wöhler Line

The shear design is performed with and without reinforcement. For the design check without shear reinforcement, it is necessary to meet the following condition.

V_{Ed, \min} / V_{Ed, \max} \geq 0

\frac{|V_{E d, m a x}|}{|V_{R d, c}|} \leq 0.5 + 0.45 \frac{|V_{E d, m i n}|}{|V_{R d, c}|} \{\begin{cases} \leq 0.9 until C 50 / 60 \\ \leq 0.8 as of C 55 / 67 \end{cases}

V_{Ed, \min} / V_{Ed, \max} < 0

|\frac{V_{Ed, \max}}{V_{Rd, c}}| \leq 0.5 - |\frac{V_{Ed, \min}}{V_{Rd, c}}|

Shear Design Without Reinforcement According to 6.8.7 (4)

In the case of the design check with shear reinforcement, the shear force stress range must not exceed the damage equivalent stress ranges according to the S-N curve specified in the standard.

∆ σ_{S w, e q u (N *)} = |V_{E d, m a x} - V_{E d, m i n}| \times \frac{\tan (θ_{f a t})}{a_{s w, V_{E d}} \times d \times 0.9}

∆ σ_{S w, R s k (N *)} = (0.35 + 0.026 \times \frac{d_{s, w, m}}{d_{s, w}}) \times ∆ σ_{R s k (N *)}

η_{S w} = |\frac{γ_{F, f a t} \times ∆ σ_{S w, e q u (N *)}}{\frac{∆ σ_{S w, R s k (N *)}}{γ_{s . f a t}}}|

Shear Design with Reinforcement, Method of Damage Equivalent Stress Range According to 6.8.5 (3)

The design checks for the concrete compressive stress and the concrete compression struts need to meet the following condition.
The concrete compressive stresses are determined from the bending and axial forces, and the concrete strut stresses from the shear and torsional forces.

E_{c d, m a x, e q u} + 0.43 \sqrt{1 - R_{e q u}} \leq 1

R_{e q u} = E_{c d, m i n, e q u} / E_{c d, m a x, e q u}

E_{c d, m i n, e q u} = σ_{c d, m i n, e q u} / f_{c d, f a t}

E_{c d, m a x, e q u} = σ_{c d, m a x, e q u} / f_{c d, f a t}

Design of Concrete Compressive Stress and Concrete Compression Strut, Method of Damage Equivalent Stress Range According to 6.8.7

Modifying Method of Damage Equivalent Stress Range

In the design configurations, you can manually adjust the following parameters. They affect the stress ranges.

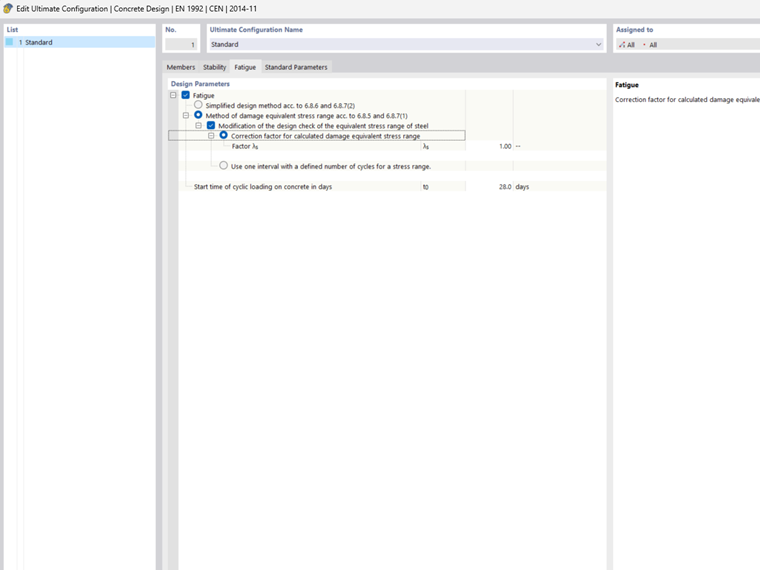
Correction Factor λ_s

This damage equivalent factor for fatigue is based on the bridge construction according to EN 1992‑2, NN.2.1, and NN.3.1. The factor increases the load-acting stress range. This factor takes into account the traffic volume, service life, and span of the supporting elements, as well as the number of lanes, traffic type, and surface roughness.

Correction Factor λs

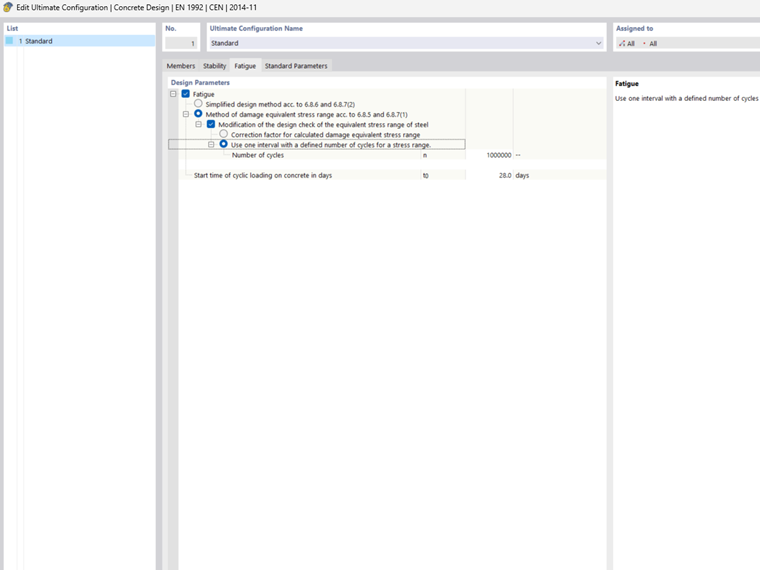
Specification of Load Cycles

The number of cycles has an influence on the allowable characteristic stress ranges according to the S-N curves in compliance with Table 6.3N.

Number of Cycles

Conclusion

The fatigue design allows you to consider the stress differences due to load changes and the material-weakening effects due to the high number of loads. With both design methods mentioned above, two options for a simplified fatigue design are available.

Note

The fatigue design check is performed by means of the extreme values of one or more result combinations. Thus, you need to create at least one result combination for the calculation.

Knowledge Base

KB 001857 | Fatigue Design According to EN 1992-1-1 in RFEM

Author

Mr. Haase is responsible for development in the area of reinforced concrete structures, and provides technical support to our customers.

References

European Committee for Standardization (CEN). (2011). Eurocode 2: Design of Concrete Structures – Part 1-1: General Rules and Rules for Buildings, EN 1992-1-1:2011-01. Berlin: Beuth Verlag GmbH.

;