The results that are related to the surfaces of the model are displayed as "Surface Quantities". These include the surface pressure, Cp coefficient results, and surface shear stress τ. You can set the type of results by clicking the
![]() ,
,
![]() , or
, or
![]() button in the "Results - Surface Quantities" area of the panel.
button in the "Results - Surface Quantities" area of the panel.
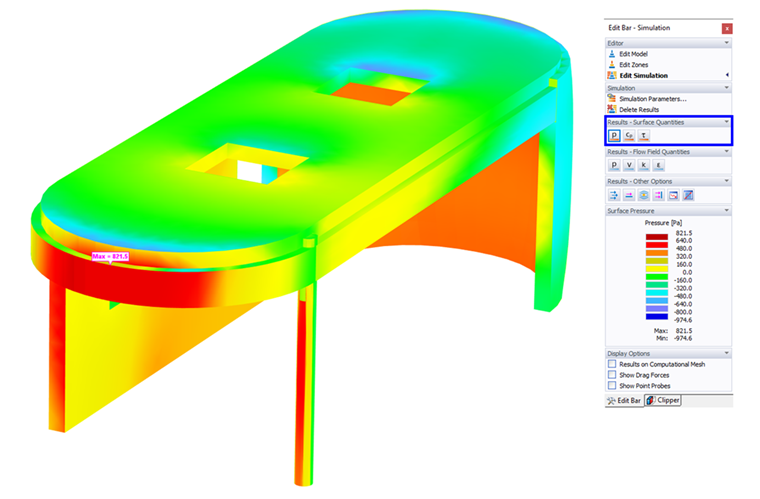
By default, the pressure due to the wind acting on the surfaces is displayed as a "Color Map": A pressure value is allocated to every point on each surface. The color assignment classifies the locations within surfaces that have specific pressure magnitudes. In the panel, the colors and respective values are represented.
The pressure acts perpendicularly on the surfaces, thus showing you drag (positive magnitudes) and lift (negative magnitudes).
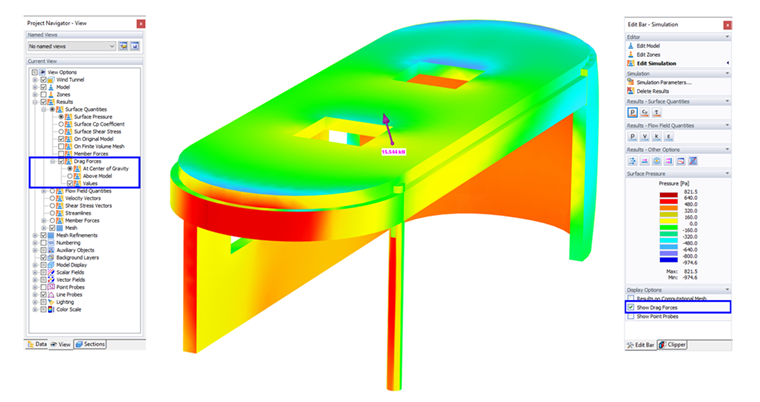
When you activate the "Show Drag Forces" option in the panel or navigator, you can review the resulting force of the wind load acting on the model and its location.
If required, you can modify the colors and assigned values (see Chapter Color Map).
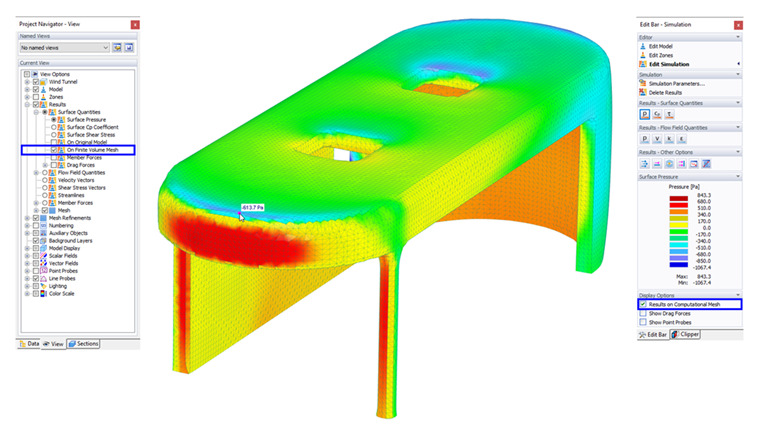
When you activate the "Results on Finite Volume Mesh" option in the panel or navigator, the surface pressure results are displayed on the mesh featuring the finite volumes used for the calculation. Thus, you can check how openings or connections of beams are treated in the simulation, for example.
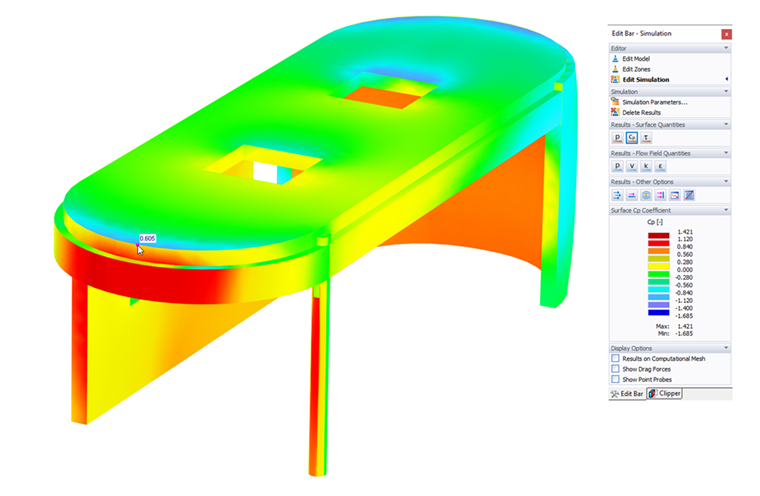
Surface Cp Coefficient
These values show the pressure coefficients that represent the relation between the static pressure and the stagnation pressure.
The coefficient Cp is useful to represent the pressure as a dimensionless quantity, which describes the relative pressures throughout a flow field. The formula is
|
p |
Static pressure |
|
p∞ |
Static pressure in the freestream |
|
ρ |
Fluid density (homogeneous and incompressible flow) |
|
v∞ |
Freestream velocity of the fluid |
where the freestream velocity v∞ is assumed as a value occurring at the top edge of the model. It is very useful to represent pressure in terms of a dimensionless quantity. More at Wikipedia.
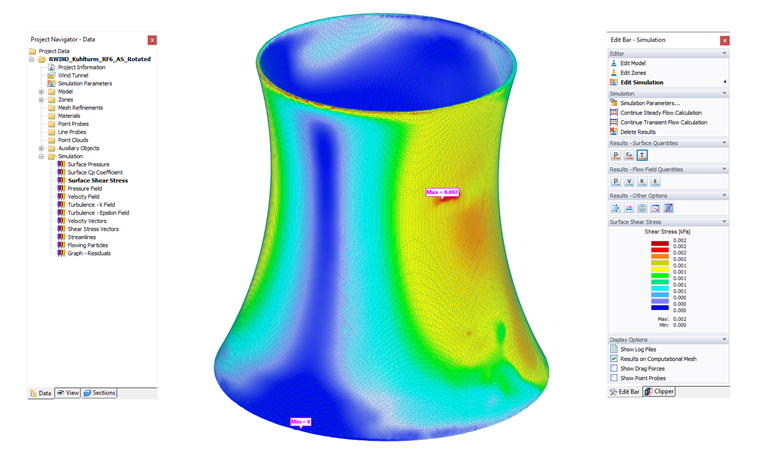
Surface Shear Stress
These results are only available for Steady Flow simulation and must be enabled in the Advanced options before calculation.
Shearing forces act differently in fluids than in solids, where the resistance to a shear deformation depends on the deformation itself. Resistance to the action of shearing forces in a fluid appears only when the fluid is in motion. The shear stress τω is a function of the shear rate gradient ∂u/∂y and dynamic viscosity, which is the property of a fluid to resist the growth of shear strain. The form of the relationship between shear stress and strain rate (shear rate gradient) depends on the fluid; for a Newtonian fluid, the shear stress is a stress proportional to the strain rate:
In the general form of Newton's constitutive law, the shear stress is proportional to the flow velocity gradient (second-order tensor); then, the equation takes the form:
More about surface shear stress and its implementation in RWIND 3 can be found here OpenFoam.