Veličiny plochy

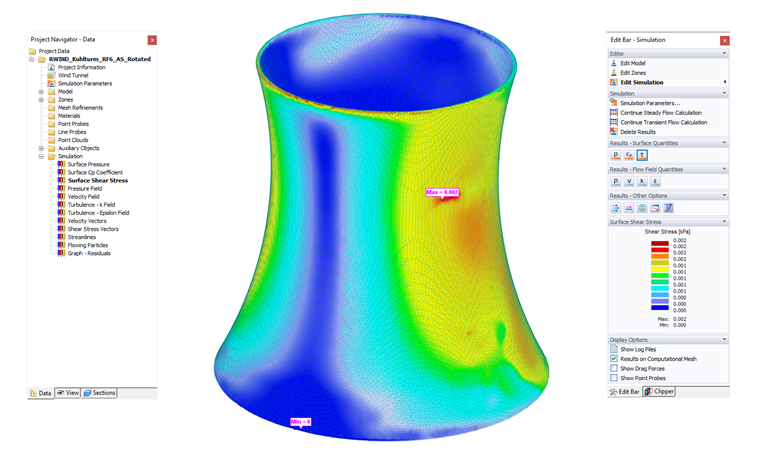
Výsledky, které se vztahují k plochám modelu, se zobrazují jako „Veličiny plochy“. Mezi ně patří tlak na povrchu, výsledky koeficientu C_p a smykové napětí na povrchu τ. Typ výsledků můžete nastavit kliknutím na tlačítko , nebo v oblasti „Výsledky – Veličiny na povrchu“ panelu.

Veličiny plochy, Plošný tlak

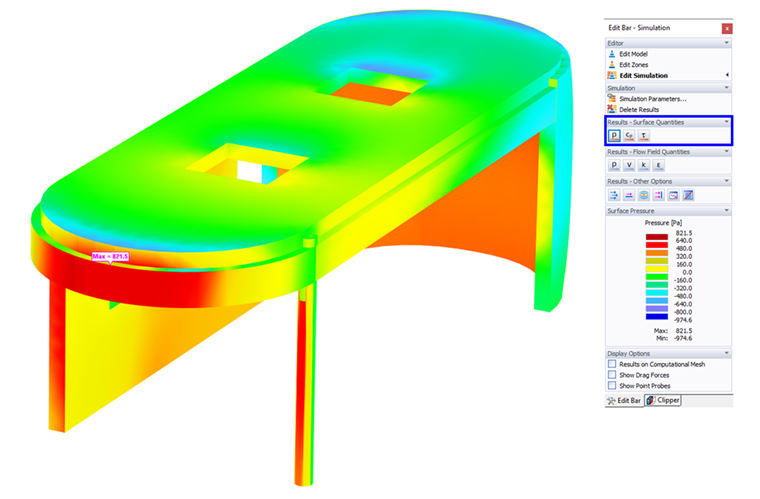
Standardně se tlak způsobený působením větru na plochy zobrazuje jako „Barevná mapa“: Každému bodu na každé ploše je přiřazena hodnota tlaku. Přiřazení barev klasifikuje místa v rámci ploch, která mají specifické velikosti tlaku. V panelu jsou zobrazeny barvy a příslušné hodnoty.

Tlak působí kolmo na plochy, čímž se zobrazí odpor (kladné hodnoty) a vztlak (záporné hodnoty).

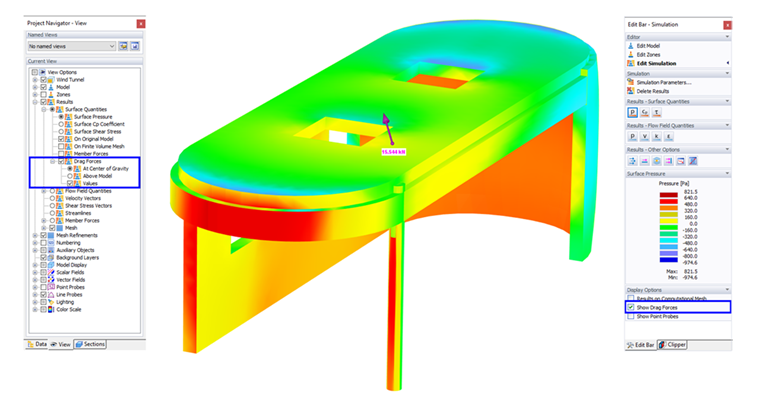
Pokud v panelu nebo navigátoru aktivujete možnost „Zobrazit odporové síly“, můžete zkontrolovat výslednou sílu zatížení větrem působící na model a její polohu.

Plošný tlak s výslednou odporovou silou

V případě potřeby můžete barvy a přiřazené hodnoty změnit (viz kapitola Barevná mapa).

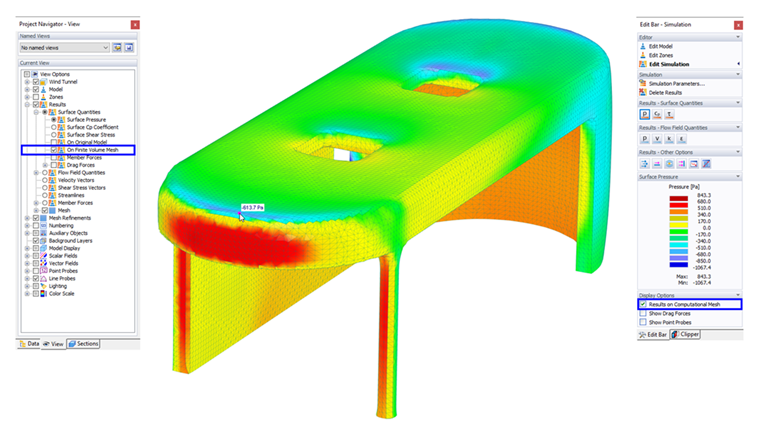
Pokud v panelu nebo navigátoru aktivujete volbu „Výsledky na síti konečných objemů“, zobrazí se výsledky tlaku na plochách na síti s konečnými objemy použitými pro výpočet. Můžete tak například zkontrolovat, jak jsou v simulaci zpracovány otvory nebo spoje nosníků.

Výsledky na síti konečných objemů

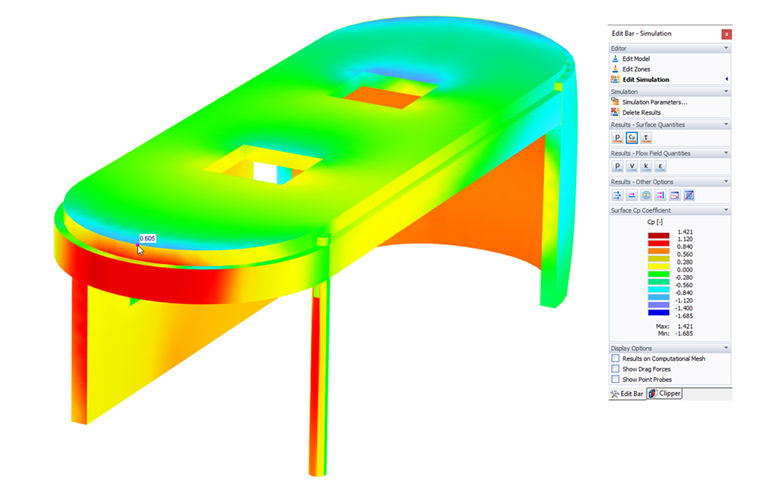
Koeficient povrchu Cp

Součinitel Cp plochy

Tyto hodnoty udávají tlakové koeficienty, které představují vztah mezi statickým tlakem a tlakem v místě stagnace.

Koeficient C_p je užitečný pro vyjádření tlaku jako bezrozměrné veličiny, která popisuje relativní tlaky v celém proudovém poli. Vzorec je

kde je rychlost volného proudu v_∞ považována za hodnotu vyskytující se na horním okraji modelu. Je velmi užitečné vyjádřit tlak jako bezrozměrnou veličinu. Více na Wikipedia.

Napětí ve smyku na ploše

Tyto výsledky jsou k dispozici pouze pro simulaci Steady Flow a musí být před výpočtem povoleny v Advanced options.

Smykové napětí plochy

Smykové síly působí v tekutinách jinak než v tělesech, kde odolnost proti smykové deformaci závisí na samotné deformaci. Odolnost proti účinku smykových sil v tekutině se projevuje pouze tehdy, když je tekutina v pohybu. Napětí ve smyku τ_ω je funkcí gradientu smykové rychlosti ∂u/∂y a dynamické viskozity, která je vlastností tekutiny odolávat růstu smykového ochabnutí. Tvar vztahu mezi napětím ve smyku a rychlostí přetvoření (gradientem smykové rychlosti) závisí na tekutině; u newtonovské tekutiny je napětí ve smyku napětím úměrným rychlosti přetvoření:

V obecné podobě Newtonova konstitutivního zákona je smykové napětí úměrné gradientu rychlosti proudění (tenzor druhého řádu); rovnice pak má tvar:

Více informací o smykovém napětí na povrchu a jeho implementaci v programu RWIND 3 naleznete zde OpenFoam.