Эта модель для учета участия бетона при растяжении между трещинами основана на определенной линии напряжений-деформаций бетона в области растяжения (параболо-прямоугольная диаграмма).
Основные предположения подхода Хсу и Мо [1] можно резюмировать следующим образом:
- До достижения деформации трещины εcr или расчетного напряжения трещины бетона fcr действует полное участие бетона при растяжении. Отношение напряжения к деформации показывает линейное поведение.
- С началом трещинообразования проявляется спад с выпуклым (конкавным) характером отношения напряжения к деформации.
- Сильно сниженное жесткое участие бетона в растянутой зоне остается.
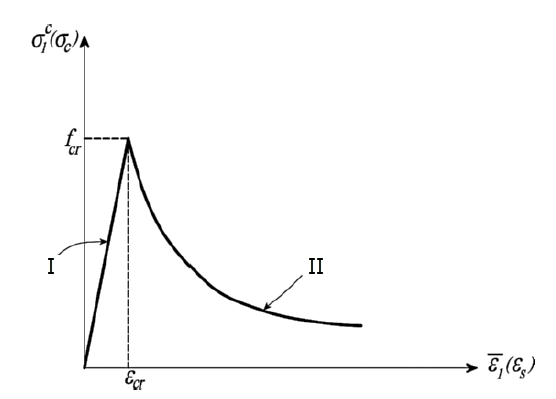
В заключение это означает, что отношение напряжение-деформация для растяжения можно разделить на два участка. До трещины связь между напряжением и деформацией в основном линейная. После трещины происходит значительное снижение прочности. Угасающая кривая имеет вогнутый (конкавный) характер. В ниспадающей ветви бетон потрескался, и бетонное растягивающее напряжение σc1 и деформация ε1 значительно отличаются от тех, что до трещины. σc1 определяется как среднее (размазанное) бетонное растягивающее напряжение, а ε1 — как средняя (размазанная) бетонная деформация растяжения. Следующее изображение показывает описанную зависимость напряжения от деформации для армированного бетона в области растяжения с учетом напряжения укрепления по подходу Хсу и Мо.
Линия напряжения-деформации в области растяжения может быть описана по [1] с помощью следующих уравнений.
- Для 0 < ε < εcr
|
|
Средняя (размытие) деформация трещин по Хсу и Мо |
|
|
Модуль упругости бетона |
- Для ε > εcr
|
|
Деформация трещины бетона |
|
|
Расчётная напряжённость трещин в бетоне |
|
|
Средняя (сглаженная) деформация трещины по Хсу и Мо |
|
|
Показатель степени для управления функцией |
В RFEM 6 к кривой добавлен параметр εct,max, с помощью которого можно ограничить прочность на растяжение. С деформации εct,max прочность на растяжение снижается до нуля.