Tento model pro zachycení přispění betonu při tahu mezi trhlinami je založen na definované napěťově-deformační čáře betonu v tažené oblasti (parabola-oblouk-dijagram).
Základní předpoklady přístupu Hsu a Mo [1] lze shrnout následovně:
- Až do dosažení trhlinového přetvoření εcr nebo vypočteného trhlinového napětí betonu fcr je plné přispění betonu při tahu. Napěťově-deformační vztah vykazuje lineární chování.
- S počátkem tvorby trhlin se projevuje klesající konkávní průběh napěťově-deformačního vztahu.
- Velmi omezené tuhé přispění betonu v tažené oblasti zůstává.
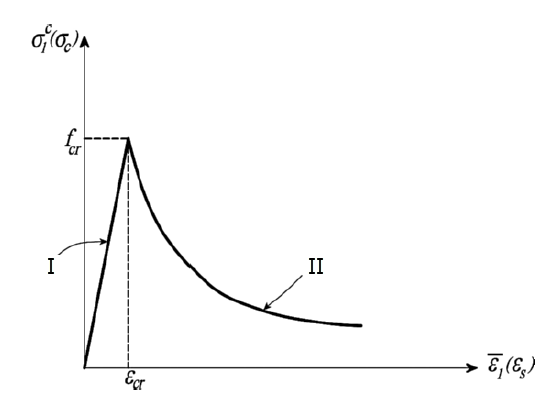
Souhrnem to znamená, že napěťově-deformační vztah pro tahové zatížení lze rozdělit do dvou oblastí. Před trhlinou je vztah mezi napětím a přetvořením v podstatě lineární. Po trhlině dochází k výraznému poklesu pevnosti. Klesající křivka vykazuje konkávní průběh. Na sestupné větvi je beton trhlinami, a betonové tahové napětí σc1 a betonové tahové přetvoření ε1 se výrazně liší od těch před trhlinou. σc1 je definováno jako střední (roztírané) betonové tahové napětí a ε1 je střední (roztírané) betonové tahové přetvoření. Následující obrázek ukazuje popsaný průběh napěťově-deformačního vztahu pro vyztužený beton v tažené oblasti s ohledem na Tension Stiffening podle přístupu Hsu a Mo.
Napěťově-deformační čára v tažené oblasti může být podle [1] popsána následujícími rovnicemi.
- Pro 0 < ε < εcr
|
|
Střední (rozptýlená) deformace trhlin podle Hsu a Mo |
|
|
Modul pružnosti betonu |
- Pro ε > εcr
|
|
Deformace trhlin betonu |
|
|
Výpočtové napětí trhlin v betonu |
|
|
Průměrné (rozmazané) tahové napětí trhliny podle Hsu a Mo |
|
|
Exponent pro ovládání průběhu funkce |
V RFEM 6 je průběh křivky doplněn o parametr εct,max, kterým lze omezit tahovou pevnost. Od přetvoření εct,max je tahová pevnost snížena na nulu.