Стержни
Внутренне для метода нелинейного расчета выполняется разбиение поперечного сечения на сетку, где отдельным элементам присваиваются разные материалы (армирование и бетон), и отдельные бетонные элементы во время расчета могут принимать разные жесткости (раскрытие трещин в бетоне).
Сетку метода конечных элементов (МКЭ) для нелинейного анализа можно просмотреть в диалоговом окне поперечного сечения и настроить её плотность. Следующая иллюстрация показывает соответствующий диалог ввода.
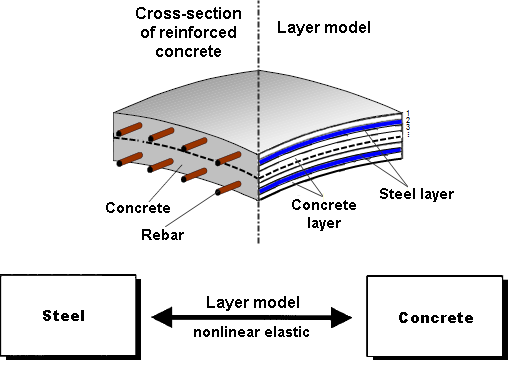
Плоскости
Внутренне для метода нелинейного расчета элемент конечного элемента (КЭ) отображается слоями, где отдельным слоям присваиваются разные материалы (армирование и бетон), и отдельные бетонные слои во время расчета могут принимать разные жесткости (раскрытие трещин в бетоне).
Методы интеграции
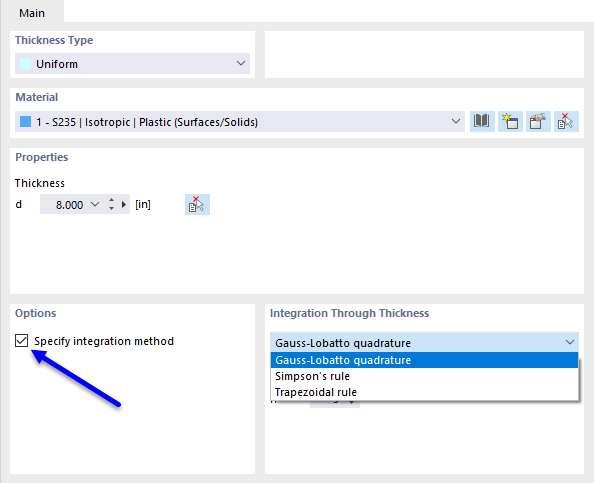
Стандартный метод интеграции для плоскостей в RFEM — это квадратура Гаусса-Лобатто с девятью точками интеграции. Этот параметр по умолчанию достаточно для большинства случаев. Чтобы особенно точно отображать нелинейные кривые напряжение-деформация, может быть целесообразно увеличить количество точек интеграции. Именно поэтому при использовании нелинейного материала возможно задать количество точек интеграции в каждом слое между тремя и 99 точками. Обратите внимание, что увеличение количества точек интеграции связано с увеличением времени расчета.
Доступны следующие три метода интеграции на выбор.
- Квадратура Гаусса-Лобатто
- Правило Симпсона
- Правило трапеций
Дальнейшее описание методов интеграции приведено в руководстве по многослойным плоскостям в следующей связанной главе Теория: Методы интеграции.
Метод интеграции можно задать по толщине плоскости. На следующей иллюстрации показано соответствующее диалоговое окно ввода.
Обзор методов с примером представлен в технической статье Влияние различных методов интеграции на расчет сталефибробетонной плиты .