TS według Hsu i Mo

Ten model do uchwycenia udziału betonu w rozciąganiu między pęknięciami opiera się na zdefiniowanej linii naprężenie-odkształcenie betonu w zakresie rozciągania (parabola-prostokąt).

Podstawowe założenia podejścia Hsu i Mo [1] można podsumować w następujący sposób:

• Do momentu osiągnięcia odkształcenia przy pęknięciu ε_cr lub obliczeniowego naprężenia betonu przy pęknięciu f_cr, istnieje pełen udział betonu w rozciąganiu. Związek naprężenie-odkształcenie wykazuje liniowe zachowanie.
• Z początkiem formowania się pęknięć pojawia się malejący konkawowy przebieg zależności naprężenie-odkształcenie.
• Istnieje znacznie zredukowane usztywniające oddziaływanie betonu w strefie rozciągania.

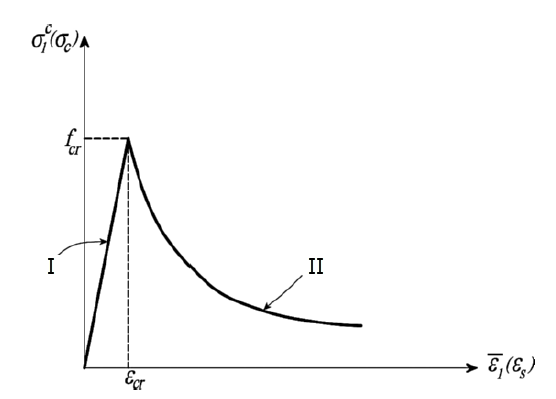
Podsumowując, oznacza to, że związek naprężenie-odkształcenie dla obciążenia rozciągającego można podzielić na dwa obszary. Przed pęknięciem związek między naprężeniem a odkształceniem jest zasadniczo liniowy. Po pęknięciu następuje silny spadek wytrzymałości. Opadająca krzywa wykazuje przebieg konkawowy. Na opadającej gałęzi beton jest pęknięty, a naprężenie rozciągające betonu σ^c₁ i odkształcenie rozciągające betonu ε₁ wyraźnie różnią się od tych przed pęknięciem. σ^c₁ jest zdefiniowane jako średnie (rozmyte) naprężenie rozciągające betonu, a ε₁ jest średnim (rozmytym) odkształceniem rozciągającym betonu. Poniższy rysunek przedstawia opisany przebieg zależności naprężenie-odkształcenie dla zbrojonego betonu w zakresie rozciągania, uwzględniając Tension Stiffening według podejścia Hsu i Mo.

Wykres naprężenie-odkształcenie betonu przy rozciąganiu

Linię naprężenie-odkształcenie w zakresie rozciągania można opisać według [1] za pomocą następujących równań:

• Dla 0 < ε < ε_cr

• Dla ε > ε_cr

W RFEM 6 przebieg krzywej uzupełniony jest o parametr ε_ct,max, za pomocą którego można ograniczyć wytrzymałość na rozciąganie. Od odkształcenia ε_ct,max wytrzymałość na rozciąganie zostaje zredukowana do zera.