Онлайн-руководства RFEM 6 / RSTAB 9 | Расчёт железобетонных конструкций

Назад к руководствам онлайн

415x

005936

Ann-Kathrin Dannwerth, B.Sc.

2025-01-23

Выбрать руководство

Обзор

Аддон Расчёт железобетонных конструкций

Основы теории

Параметры анализа

Расчетные характеристики

Расчет

Результаты

Таблицы для расчета бетона
Графика для расчета бетона
- Расчётные проверки
  
  Стержни
  
  Репрезентанты стержней
  
  Поверхности
  
  Узлы
- Арматура
  
  Стержни
  
  Репрезентанты стержней
  
  Поверхности
  
  Узлы
Подробный вывод результатов

Документация

Прямой расчёт деформаций

с использованием метода эффективной жесткости (ESM)

1. Описание теоретической основы

Для анализа деформации в рамках бетонного армирования используется аналитический метод для 2D-структур и 1D-элементов, подверженных воздействию нормальных сил и моментов изгиба. Он основан на расчете эффективных жесткостей (метод эффективной жесткости) на уровне сечения с учетом состояния трещин, а также эффектов, таких как напряженное упрочнение и простые долговременные эффекты (усадка и ползучесть).

1.1. Основные предположения по материалам и геометрии

Для прямого анализа деформации в бетонном армировании применяется линейно-упругое поведение при сжатии и линейно-упругое поведение до достижения прочности на растяжение. Такие предположения достаточны для проверки пригодности. Если напряжения превышают прочность бетона на сжатие, развитие повреждений происходит в соответствии с EN 1992-1-1, раздел 7.3.4. Расчет основан на простом изотропном модели механики разрушения, определенном индивидуально для двух направлений армирования. Согласно EN 1992-1-1, эффективная матрица жесткости материала вычисляется путем интерполяции между нерастресканным состоянием (Состояние I) и растресканным состоянием (Состояние II) в соответствии с разделом 7.4.3, уравнение (7.18). Таким образом, железобетон моделируется как ортотропный материал. При этом учитываются такие эффекты, как напряженное упрочнение и простые долговременные эффекты (усадка и ползучесть). Расчет матриц жесткости материала осуществляется для типов моделей 2D-XY (u_z / φ_x / φ_y) и 3D. В 3D-модели дополнительно учитывается влияние эксцентриситетов идеальных центров тяжести в матрице жесткости.

1.2. Проектные внутренние силы

Как описано выше, расчет жесткости основан на линейно-упругих предположениях. Внутренние силы преобразуются ортогонально по направлению армирования ф и двум поверхностям s (верхняя и нижняя). Полученные внутренние силы - изгибающие моменты m_s,ф и нормальные силы n_s,ф (крутящие моменты устраняются преобразованием) - зависят от: (a) типа модели; (b) метода расчета; (c) критерия классификации.

1.3. Критическая поверхность

Для определения критической поверхности каждое направление армирования ф рассматривается отдельно. Стрессовое состояние анализируется на нижней поверхности (по локальной +z оси) и на верхней поверхности (по локальной -z оси). Поверхность с большим бетонным растягивающим напряжением считается основной. Внутренние силы на критических поверхностях обозначаются как n_ф и m_ф.

Нормальная сила n_ф,s, преобразованная в направлении армирования ф, имеет одинаковое значение для обеих поверхностей (n_ф = n_ф,верх = n_ф,низ). Поэтому нормальные силы не принимаются в расчет критической поверхности; только изгибающие моменты рассматриваются для нахождения главной поверхности. Знаки изгибных моментов m_ф,s определяются в зависимости от того, вызывают ли они растяжение или сжатие на соответствующей поверхности. Критическая поверхность - это та, на которой действует больший изгибающий момент (т.е. более подвергнутая растяжению поверхность).

При расчете жесткостей учитываются только внутренние силы n_ф и m_ф на критической поверхности. До настоящего момента термин "нижняя поверхность" относился к локальной +z оси. Далее "нижняя поверхность" будет относиться к главной стороне поверхности.

1.4. Свойства сечения

Свойства сечения определяются для обоих направлений армирования и для обоих состояний сечения c (растресканное/нерастресканное). Для состояния I (нерастресканное сечение) принимается линейно-упругое поведение бетона при растяжении. Для состояния II (растресканное сечение) прочность бетона на растяжение не учитывается.

Расчет геометрических параметров для состояния I независим от внутренних сил, что позволяет непосредственно производить расчет. Для состояния II глубина нейтральной оси рассчитывается итерационно. По численным причинам программа использует минимальную степень армирования ρ_min = 10^-4 для обеих решающих поверхностей (верхней и нижней), но только при положительной нормальной составляющей. Это означает, что при отсутствии армирования принимается виртуальная минимальная площадь армирования. Такое малое значение не оказывает значительного влияния на результаты (жесткости).

Рассчитанные идеальные свойства сечения (по отношению к бетонному сечению) в направлении армирования ф и для состояния трещин c следующие: (a) Момент инерции относительно идеального центра тяжести I_c,ф; (b) Момент инерции относительно геометрического центра тяжести сечения I_0,c,ф; (c) Площадь сечения A_c,ф; (d) Эксцентриситет идеального центра тяжести e_c,ф.

1.5. Долговременные эффекты

Усадка и ползучесть являются зависящими от времени свойствами бетона. Согласно EN 1992-1-1, долговременные эффекты должны учитываться отдельно.

1.5.1. Ползучесть

Эффекты ползучести учитываются путем снижения модуля упругости бетона E_c с использованием эффективного коэффициента ползучести ϕ_eff согласно EN 1992-1-1, уравнение (7.20):

E_{c, eff} = \frac{E_{cm}}{1 + φ}

Эффективный модуль упругости по по 7.4.3 (5) форм. 7,20

1.5.2. Усадка

В расчете прогиба согласно EN 1992-1-1, есть два аспекта, которые подвержены влиянию усадки.

1.5.2.1. Снижение жесткости материала Жесткость материала в каждом направлении армирования φ уменьшается с использованием так называемого коэффициента влияния усадки k_sh,c,φ. Для обоих состояний трещин c (растресканное/нерастресканное) нормальные силы усадки n_sh,c,φ и изгибающие моменты m_sh,c,φ определяются из свободной деформации усадки ε_sh:

n_{sh, ϕ} = - ε_{sh} \cdot E_{s} (a_{s 1} + a_{s 2})

m_{sh, ϕ} = n_{sh} \cdot e_{sh}

m_sh,φ	Дополнительный момент от усадки в центре тяжести идеального сечения по направлению армирования ф
n_sh,φ	Добавочная осевая сила вследствие усадки в направлении арматуры ф
a_S1	Нижняя поверхность арматуры
a_S2	Верхняя поверхность арматуры
E_s	Модуль упругости арматурной стали
ε_sh	Усадочная деформация
e_sh	Экцентричность усадочных сил (состояние I и состояние II) от центра тяжести идеального сечения

Дополнительная осевая сила и момент из-за усадки в арматуре

Диаграмма, показывающая распределение усилий Nsh и Msh по конструктивному элементу.

Анализ внутренних сил: N_sh и M_sh

Рис. 1.1: Внутренние силы n_sh,ф и m_sh,ф С использованием этих внутренних сил из усадки рассчитывается дополнительная кривизна κ_sh,c,ф в анализируемой точке – без учета влияния окружающей модели. Затем рассчитывается коэффициент влияния усадки

k_{sh, c, ϕ} = (κ_{sh, c, ϕ} + κ_{ϕ}) / κ_{ϕ}

κ_ф	Изгиб, вызванный внешней нагрузкой без влияния усадки в направлении армирования
κ_{sh, c, ϕ}	Кривизна, вызванная усадкой (и расположением армирования) без влияния ползучести в направлении армирования

Кривизна, вызванная усадкой (и расположение арматуры), без влияния ползучести в направлении арматуры

Коэффициент k_sh,c,ф ограничен диапазоном k_sh,c,ф ∈ (1, 100). Таким образом, k_sh,c,ф не должен уменьшать жесткость более чем в 100 раз (по численным и физическим причинам). Минимальное значение k_sh,c,ф = 1,0 означает, что влияние усадки не может быть учтено, если оно имеет противоположное направление по отношению к кривизне κ_d, вызванной нагрузкой. Если усадка отключена, коэффициент k_sh,c,ф = 1,0. Влияние усадки на мембранную жесткость не учитывается.

1.5.2.2. Расчет распределительного коэффициента Второй эффект усадки касается расчета распределительного коэффициента (параметра повреждения) ζ в соответствии с EN 1992-1-1, раздел 7.4.3, уравнение (7.18). Следующая глава описывает распределительный коэффициент в деталях.

1.6. Распределительный коэффициент

Расчет распределительного коэффициента ζ_d представлен для направления армирования ф. Сначала программа рассчитывает максимальное растягивающее напряжение бетона σ_max,ф при предположении линейно-упругого поведения материала. Если долговременные эффекты (ползучесть или усадка) активированы, максимальное напряжение должно быть рассчитано дважды, в противном случае - один раз.

Краткосрочный расчет: Проверяет, появляются ли трещины сразу после нагрузки. Долгосрочный расчет: Учитывает поведение трещин под влиянием ползучести или усадки в конце рассматриваемого периода.

Этапы расчета: При активированной ползучести: Рассчитываются краткосрочные геометрические параметры и максимальное напряжение. При активированной усадке: Необходимо лишь заново рассчитать краткосрочное напряжение. Затем окончательное максимальное напряжение σ_max,ф определяется как максимум из долгосрочного напряжения σ_max,lt,ф и краткосрочного напряжения σ_max,st,ф.

с_{\max, lt, ϕ} = \frac{n_{ϕ} + n_{sh, ϕ}}{A_{I, ϕ}} + \frac{m_{ϕ} - n_{ϕ} \cdot (z_{I, ϕ} - h / 2) + m_{sh, I, ϕ}}{I_{I, ϕ} \cdot (h - z_{I, ϕ})}

с_{\max, st, ϕ} = \frac{n_{ϕ}}{A_{I, st, ϕ}} + \frac{m_{ϕ} - n_{ϕ} \cdot (z_{I, st, ϕ} - h / 2)}{I_{I, st, ϕ} \cdot (h - z_{I, st, ϕ})}

с_{\max, ϕ} = \max (с_{\max, st, ϕ}, с_{\max, lt, ϕ})

n_φ	Усилие растяжения от внешней нагрузки
n_sh,φ	Дополнительная продольная сила из-за усадки
m_φ	Момент из-за внешней нагрузки
m_sh,I,ϕ	Дополнительный момент из-за усадки в состоянии I
h	Глубина сечения
z_I,ф	Расстояние центра тяжести идеального сечения от поверхности бетона в сжатии в состоянии I
A_{I, φ}	Площадь идеального сечения в состоянии I
I_I,φ	Идеальный момент инерции в стадии I
z_I,ст,ф	Расстояние центра тяжести идеального сечения от бетонной поверхности при сжатии в состоянии I по направлению арматуры ф, кратковременная нагрузка
A_I,st,ф	Площадь идеального сечения в состоянии I в направлении арматуры ф, кратковременная нагрузка
I_I,st,ф	Идеальный момент инерции в состоянии I в направлении армирования ф, кратковременная нагрузка

Окончательное максимальное напряжение

Влияние сил усадки на максимальное растягивающее напряжение σ_max,ф учитывается за счет дополнительных внутренних сил из усадки. Расчет распределительного коэффициента ζ_d,ф зависит от того, учитывается ли напряженное упрочнение согласно EN 1992-1-1 в расчете деформации.

1.6.1. Распределительный коэффициент ζ_d,ф с учетом напряженного упрочнения

Для σ_{\max, ф} > f_{ctm} : ζ_{d, ϕ} = 1 - β \cdot {(\frac{fctm}{σ_{maxϕ}})}^{n}

и для σ_{\max, ф} \leq f_{ctm} : ζ_{d, ϕ} = 0

β	Параметр с учётом длительности нагрузки
f_ctm	Средняя прочность на растяжение
n	= 2 для EN 1992-1-1

Коэффициент распределения ζ с учётом натяжного армирования

1.6.2. Распределительный коэффициент ζ_d,ф без учета напряженного упрочнения

1.6.3. Определение состояния трещин

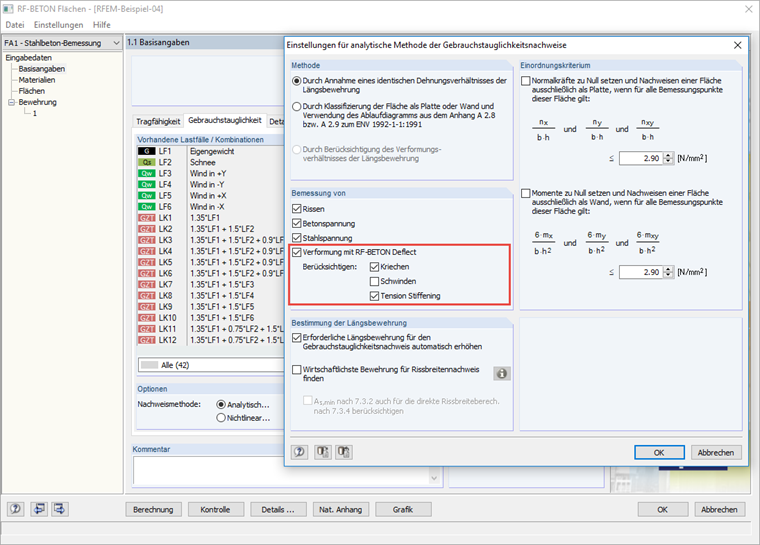
Определение состояния трещин может быть настроено в конфигурации пригодности к эксплуатации (Serviceability Configuration). Доступны следующие варианты: (a) Состояние трещин рассчитывается на основе соответствующей нагрузки; (b) Состояние трещин на основе соответствующей характерной комбинации (CO) ситуации расчета SLS; (c) Состояние трещин определено как оболочка из всех ситуаций расчета SLS; (d) Состояние трещин независимо от нагрузки.

Интерфейс отображения конфигурации для определения состояние трещин с техническими параметрами.

Конфигурация пригодности к эксплуатации | Обнаружение состояния трещин

Рис. 1.2: Конфигурация пригодности к эксплуатации Если выбрана опция Состояние трещин рассчитывается на основе соответствующей нагрузки, состояние трещин (распределительный коэффициент ζ_d) рассчитывается только на основе текущей нагрузки (комбинации нагрузок). Если выбрана опция Состояние трещин на основе соответствующей характерной комбинации (CO) ситуации расчета SLS, распределительный коэффициент ζ_d рассчитывается как максимум из всех соответствующих нагрузок. Соответствующие нагрузки могут быть заданы при определении комбинирования нагрузок.

Иллюстрация соответствующей комбинации нагрузок с техническими аннотациями для взаимодействия нагрузок.

Соответствующее сочетание нагрузок

Рис. 1.3: Соответствующие нагрузки Если выбрана опция Состояние трещин определено как оболочка из всех ситуаций расчета SLS, распределительный коэффициент ζ_d рассчитывается как максимум из всех ситуаций расчета. Если выбрана опция Состояние трещин независимо от нагрузки, распределительный коэффициент всегда равен 1,0.

1.6.4. Ситуации расчета SLS

Обычно прогиб рассчитывается для квазипостоянных нагрузок. Тем не менее, возможно выбрать желаемые расчетные ситуации (в конфигурации пригодности к эксплуатации, опция Пользовательское назначение типа ситуации расчета), для которых должен быть рассчитан прогиб. Могут быть выбраны следующие типы ситуаций расчета пригодности к эксплуатации: - Квазипостоянная, - Частая, - Характеристическая. Для каждого типа может быть задано предельное значение прогиба (см. Рис. 1.2). Кроме того, желаемые ситуации расчета также определяются для бетонного армирования.

Интерфейс с настраиваемыми параметрами расчёта железобетона и техническими опциями

Design Settings for Concrete Design

Рис. 1.4: Настройка ситуаций расчета для бетонного армирования Для определения состояния трещин (особенно при выборе, определяются ли они из соответствующих нагрузок или из всех ситуаций расчета пригодности к эксплуатации) настройка в бетонном армировании имеет важное значение. Другими словами: - Если ситуация расчета отключена в конфигурации пригодности к эксплуатации, но активирована в настройке бетонного армирования, то она учитывается. - Если ситуация расчета активирована в конфигурации пригодности к эксплуатации, но отключена настройки бетонного армирования, то она не учитывается.

1.7. Свойства сечения для анализа деформации

В матрице жесткости материала D для анализа деформации программе необходимы свойства сечения в каждом направлении армирования, зависящие от состояния трещин. Эти свойства: (a) Момент инерции относительно идеального центра тяжести I_ф; (b) Момент инерции относительно геометрического центра тяжести сечения I_0,c; (c) Идеальная площадь сечения A_ф; (d) Эксцентриситет идеального центра тяжести e_ф относительно геометрического центра тяжести. Среднее удлинение ε_ф и средняя кривизна κ_ф рассчитываются путем интерполяции между растресканным и нерастресканным состоянием согласно EN 1992-1-1, уравнение (7.18):

ε_{ϕ} = ζ_{d, ϕ} \cdot ε_{II, ϕ} + (1 - ζ_{d, ϕ}) \cdot ε_{I, ϕ}

κ_{ϕ} = ζ_{d, ϕ} \cdot κ_{II, ϕ} + (1 - ζ_{d, ϕ}) \cdot κ_{I, ϕ}

Средняя деформация и средняя кривизна

Деформация в нерастресканном и растресканном состоянии c (Состояние I и II) рассчитывается по следующим уравнениям:

ε_{c, ϕ} = \frac{n_{ϕ}}{E \cdot A_{c, ϕ}}

κ_{c, ϕ} = k_{sh, c, ϕ} \cdot \frac{m_{ϕ} - n_{ϕ} \cdot e_{c, ϕ}}{E \cdot I_{c, ϕ}}

Деформация в состоянии без трещин и с трещинами c

Идеальные свойства сечения рассчитываются относительно идеального центра тяжести сечения. Влияние усадки учитывается через фактор k_sh,c,ф:

A_{f, ϕ} = \frac{A_{I, ϕ} \cdot A_{II, ϕ}}{ζ_{d, ϕ} \cdot A_{I, ϕ} + (1 - ζ_{d, ϕ}) \cdot A_{II, ϕ}}

I_{f, ϕ} = \frac{I_{I, ϕ} \cdot I_{II, ϕ}}{ζ_{d, ϕ} \cdot I_{I, ϕ} \cdot k_{sh, II, ϕ} + (1 - ζ_{d, ϕ}) \cdot I_{II, ϕ} \cdot k_{sh, I, ϕ}}

Идеальные характеристики сечения с учетом усадки

Если нормальная сила отлична от нуля, свойства сечения рассчитываются относительно геометрического центра тяжести сечения с учетом эксцентриситета:

e_{f, φ} = \frac{m_{φ} - κ_{φ} \cdot E \cdot I_{φ}}{n_{φ}}

I_{0, f, φ} = I_{φ} + A_{φ} \cdot e_{φ}^{2}

Характеристики сечения, относящиеся к геометрическогому центру сечения при использовании эксцентриситета

1.8. Матрица жесткости материала D (стержни)

Аксиальная жесткость EA и изгибающая жесткость EI_y,0 рассчитываются только в направлении армирования ф = 1 (направление стержня) следующим образом:

{EA}_{f} = E_{c, eff} \cdot A_{f}

{EI}_{y, 0, f} = E_{c, eff} \cdot I_{y, 0, f}

Осевая жёсткость и жесткость на изгиб

1.9. Матрица жесткости материала D (поверхности)

При расчете свойств сечения начальное значение коэффициента Пуассона ν_init в обоих направлениях независимо снижается по следующему уравнению:

ν_{ϕ} = (1 - ζ_{d, ϕ}) \cdot ν_{init}

характеристики сечения

Матрица жесткости материала рассчитывается согласно теории для ортотропных поверхностей.

1.9.1. Изгибающая жесткость - пластины и оболочки

Изгибающие жесткости в направлениях армирования ф определяются следующим образом: Для оболочек:

D_{d, d} = \frac{I_{0, f, d} \cdot E_{c, eff}}{1 - ν_{1} \cdot ν_{2}}

d	= {1,2} по направлению

Жёсткости на изгиб в направлении армирования φ для оболочек

Для пластин:

D_{d, d} = \frac{I_{f, d} \cdot E_{c, eff}}{1 - ν_{1} \cdot ν_{2}}

d	= {1,2} по направлению

Жёсткость на изгиб в направлениях армирования ф для пластин

Не-диагональная компонента матрицы жесткости для пластин и оболочек идентична:

D_{1, 2} = D_{2, 1} = \sqrt{ν_{1} \cdot ν_{2} \cdot D_{1, 1} \cdot D_{2, 2}}

Недиагональный компонент матрицы жёсткости материала для пластин и оболочек

Для оболочек различия в изгибающих жесткостях за счет моментов инерции компенсируются эксцентриситетными компонентами в матрице жесткости.

1.9.2. Крутильная жесткость пластин и оболочек

Элементы матрицы жесткости для пластин и оболочек рассчитываются следующим образом:

D_{3, 3} = \frac{1 - \sqrt{v_{1} \cdot ν_{2}}}{2} \cdot \sqrt{D_{1, 1} \cdot D_{2, 2}}

Матрица жесткости для плит и оболочек

1.9.3. Сдвиговая жесткость пластин и оболочек

Элементы матрицы жесткости для сдвига не уменьшаются при анализе деформации. Они рассчитываются из модуля сдвига G идеального сечения и высоты сечения h. Выражение одинаково для оболочек и пластин:

D_{3 + d, 3 + d} = 5 / 6 \cdot G \cdot h

d	= {1,2} в зависимости от направления

Матрица жёсткости при сдвиге из данных о сдвиге

1.9.4. Мембранная жесткость оболочек

Мембранные жесткости в направлениях армирования ф рассчитываются следующим образом:

D_{5 + d, 5 + d} = \frac{A_{f, d} \cdot E_{c, eff}}{1 - ν_{1} \cdot ν_{2}}

d	= {1,2} по направлению

Мембранные жёсткости в направлениях армирования

Не-диагональная часть матрицы жесткости материала определяется следующим образом:

D_{6, 7} = D_{7, 6} = \sqrt{ν_{1} \cdot ν_{2} \cdot D_{6, 6} \cdot D_{7, 7}}

Недигональная часть матрицы жёсткости материала

Доля компонента сдвиговой жесткости равна:

D_{8, 8} = G \cdot h

Компонент жесткости при сдвиге в матрице жесткости материала

1.9.5. Эксцентриситет – оболочки

Элементы матрицы жесткости для эксцентриситета центра тяжести (идеальное сечение) в направлении армирования ф рассчитываются следующим образом:

D_{d, d + 5} = D_{d + 5, d} = D_{5 + d, 5 + d} \cdot e_{f, d}

d	= {1,2} по направлению

Элементы матрицы жёсткости эксцентриситета центра тяжести (идеальное сечение) в направлении армирования

Не-диагональная часть матрицы жесткости материала определяется следующим образом:

D_{1, 7} = \frac{\sqrt{ν_{1} \cdot ν_{2}}}{2} \cdot (e_{f, 1} + e_{f, 2}) \cdot \sqrt{D_{6, 6} \cdot D_{7, 7}}

Недиагональный компонент матрицы жесткости материала

Эксцентриситетная компонента для кручения рассчитывается следующим образом:

D_{3, 8} = \frac{1}{2} \cdot G \cdot h \cdot (e_{f, 1} + e_{f, 2})

Компоненты эксцентриситета для кручения

1.9.6. Проверка на положительную определенность

Положительная определенность матрицы жесткости материала D тестируется с помощью модифицированного (с учетом нулевых блоков) критерия Сильвестра. Если матрица жесткости D не является позитивно определенной, не-диагональные компоненты матрицы жесткости материала последовательно устанавливаются в нуль. В крайнем случае, остаются только положительные компоненты главной диагонали.

1.10. Расчет прогибов

Прогибы объекта (стержня или поверхности) определяются с использованием предварительно рассчитанной матрицы жесткости D. Определяется расчетное значение (Design Ratio) на основе прогиба и предельного значения.

1.10.1. Соответствующая нагрузка

Когда соответствующая нагрузка назначается основной нагрузке, окончательный прогиб рассчитывается как сумма отдельных значений. Основная комбинация нагрузки рассчитывается без учета зависящих от времени свойств (ползучести и усадки) и поэтому должна быть краткосрочной (частой или характерностной). Однако соответствующая комбинация нагрузки всегда рассчитывается с учетом зависящих от времени свойств и, следовательно, должна быть долгосрочной (постоянно). Если назначается более одной соответствующей нагрузки, учитывается та, для которой значение прогиба является наибольшим. Общий прогиб рассчитывается следующим образом:

u_{z} = u_{z, tot, QP, lt} + (u_{z, tot, st} - u_{z, tot, QP, st})

u_z,tot,QP,lt	Долговечный прогиб (с учётом ползучести и усадки) квазипостоянной нагрузки
u_z,tot,QP,st	Кратковременный прогиб (без ползучести и усадки) квазипостоянной нагрузки
u_z,tot,st	Краткосрочный прогиб (без учёта ползучести и усадки) текущей (частой или нормативной) нагрузки

Общий прогиб

1.11 Различия между RFEM 5 и RFEM 6

Расчет высоты бетонной зоны сжатия В RFEM 5 высота бетонной зоны сжатия рассчитывалась на основе чистой высоты сечения, тогда как в RFEM 6 используется брутто высота сечения. Этот подход обеспечивает более быстрое и наглядное выполнение расчетов, что также позволяет лучше отслеживать их результаты. Эта упрощенная методика не снижает точности расчета, что означает отсутствие значительных различий в результатах для практических применений. Таким образом, RFEM 6 предлагает более эффективное решение с неизменно точными результатами.

Коэффициент распределения армирования Коэффициент распределения, описывающий распределение напряжения по сечению, в RFEM 5 определялся исключительно на основе долговременного напряжения. Это означало, что учитывалось только напряжение, действующее на протяжении длительного времени. В RFEM 6 методика расчета была усовершенствована: теперь учитывается максимум из долговременного и кратковременного напряжения. Это изменение обеспечивает более реалистичное отображение фактических напряжений в сечении.

Исходная глава

Ограничение деформаций

Дополнительные ссылки

Modell eines Stahlbetonbalkens, der durch Kriechen und Schwinden beeinflusst wird

Прямой расчёт деформаций железобетонной балки с учётом ползучести и усадки

Настройки для расчета деформаций в RF-CONCRETE Deflect

Коэффициент распределения ζ в расчете деформаций железобетонных элементов