Модифицированное TS по Квасту и Квасту

Quast

Эта модель, которая используется для определения эффективности бетона при растяжении между трещинами, основана на заданной кривой напряжения-деформации бетона в зоне растяжения (параболическо-прямоугольная диаграмма).

Основные допущения подхода Quast' можно резюмировать следующим образом:

• полное участие бетона в растяжении до достижения деформации при образовании трещин ε_cr или расчетной прочности бетона на растяжение f_ct,R
• Сниженная доля жесткости бетона в растянутой зоне согласно существующей деформации бетона.
• Не применяется усиление при растяжении после того, как определяющая арматура начинает текучесть.

Подводя итог, это означает, что прочность на растяжение f_ct,R, используемая в расчете, не является фиксированной величиной, а относится к существующей деформации в определяющем стальном (растяжении) волокне. Максимальный предел прочности на растяжение f_ct,R уменьшается линейно до нуля, начиная с заданной деформации при образовании трещин ε_cr до достижения деформации текучести арматурной стали в определяющем стальном волокне.
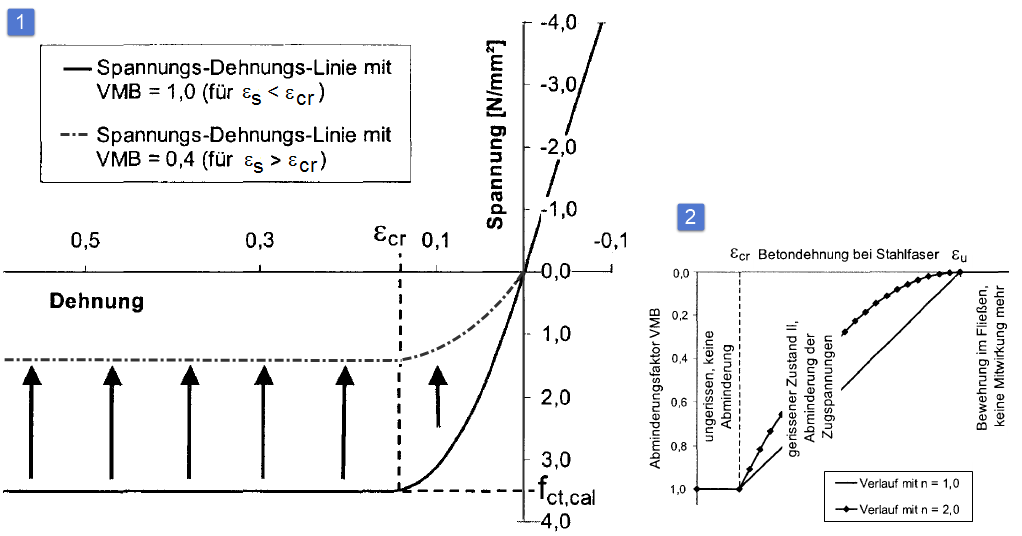
Этого можно достичь с помощью диаграммы напряжения-деформации в области растяжения бетона (параболическо-прямоугольная диаграмма), показанной на следующем рисунке, и определения понижающего коэффициента VMB (упрочнение бетона).

Диаграмма напряжение-деформация бетона на растянутой стороне с коэффициентом редукции γMB = 0.4

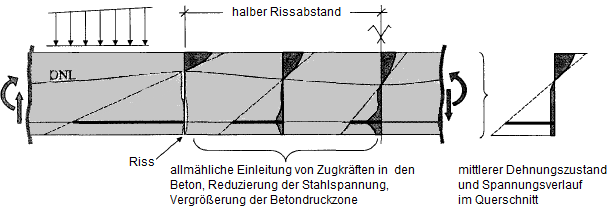
На следующем рисунке показана схема напряженного состояния при увеличении нагрузки из-за усиления жесткости при растяжении.

Напряженное состояние для увеличения нагрузки с учетом жёсткости растяжения

Диаграмма напряжения-деформации в области растяжения может быть описана с помощью следующих уравнений:

• Кривизной параболы в первой части можно управлять с помощью экспоненты n_PR.
• Экспонента должна быть подобрана таким образом, чтобы переход из зоны сжатия в зону растяжения достигается с одинаковым модулем упругости.

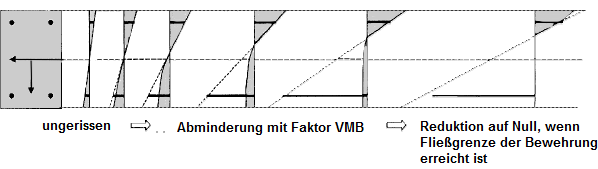
Для определения понижающего коэффициента VMB используется деформация у наиболее растянутого стального волокна. Положение точки-ориентира показано на рисунке ниже.

Тензорная диаграмма для натяжения армирования согласно Quast

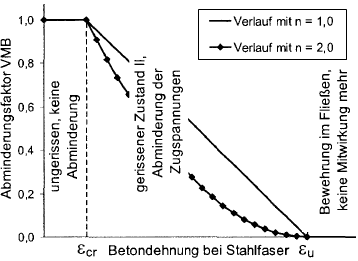
Параметр редукции VMB уменьшается с увеличением деформации стали. На диаграмме для коэффициента VMB (см. рисунок ниже) видно, что коэффициент VMB уменьшается до нуля точно в точке, где начинается текучесть арматуры.

Коэффициент редукции VMB – напряженное состояние по Квасту

Распределение для понижающего коэффициента VMB в состоянии II (ε > ε_cr ) можно контролировать с помощью экспоненты n_VMB.

• Значения от n_VMB = 1 (линейная) до n_VMB = 2 (парабола) являются эмпирическими для конструктивных элементов, подверженных изгибу.
• Кваст [3] использует в своей модели экспоненту n_VMB = 1 (линейный), благодаря чему достигается хорошее согласование при перерасчете испытаний колонны.
• Согласно Pfeifer {%><#Refer [2]]], можно описать испытания на чистое растяжение с приемлемой согласованностью при использовании n_VMB = 2.

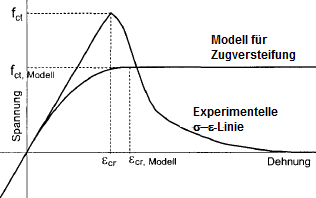
Для облегчения расчета затем можно применить параболическо-прямоугольную диаграмму для зоны растяжения бетона с трещинами. На первый взгляд, есть значительные различия по сравнению с экспериментально определенными диаграммами напряжения-деформации на растянутой стороне чистого бетона.

Упрочнение натяжением по Квасту – Сравнение моделей и лабораторных испытаний

Приведенные напряжения в железобетонном сечении при изгибе показывают, что диаграмма парабола-прямоугольник действительно лучше подходит для описания среднего значения деформаций и напряжений.
В изгибаемой балке между двумя трещинами образуется бетонное тело. Она действует как своего рода стена, в которую растягивающие силы постепенно поглощаются арматурой. Это приводит к очень неравномерному распределению напряжений и деформаций. Однако в среднем мы можем создать плоскость деформации с распределением параболы-прямоугольника, с помощью которой можно учесть среднюю кривизну.

Состояние предварительного напряжения ЖБ при изгибе

Для модели от Quast были предложены следующие расчетные значения, которые должны быть применены

• для прочности на растяжение f_ct,R

• для деформации трещин ε_cr,R

Таким образом, расчетное значение прочности на растяжение f_ct,R меньше, чем указано в Еврокоде. Это связано с описанием зависимости напряжения и деформации и определением параметра редукции VMB, при котором предполагаемое растягивающее напряжение и результирующая растягивающая сила только медленно уменьшаются после превышения растягивающей деформации. При деформации 2 ⋅ ε_cr дополнительно действует действующее растягивающее напряжение около 0,95 ⋅ f_ct,R . Таким образом, в случае изгиба можно хорошо предсказать снижение жесткости. При чистом растяжении вышеупомянутые значения f_ct,R слишком малы. Согласно Pfeifer{%://#Refer [2]]], в расчетах значений прочности на растяжение должны применяться значения из EC 2.
Значения f_ct,R = 1/20 ⋅ f_см, рекомендуемые компанией Quast [3], могут быть достигнуты при применении 60 % прочности на растяжение, указанной в EC 2. , то при применении f_ct,R = 0,6 ⋅ fctm образование трещин в сечении предсказывается слишком быстро. С другой стороны, здесь уже учитывается снижение прочности на растяжение при постоянной нагрузке (около 70%) или временное повышение нагрузки (например, кратковременное применение редкого сочетания воздействий), что приводит к повреждению растянутой зоны.
Значения отдельных расчетов для зоны растяжения бетона' можно описать следующим образом:

Модифицированный метод Кваста