Základy posouzení
Předpokladem takového posouzení je vytvoření odpovídajícího výpočetního modelu a jeho porovnání s údaji v normě, případně s údaji ve stavebních technických osvědčeních [3] vydaných k jednotlivým produktům.
Verifikace výpočetního modelu
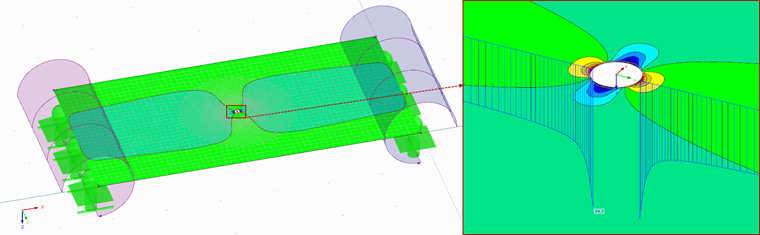
Jako první krok je třeba posoudit kvalitu výsledků na vrtaném otvoru. Je přitom důležité nastavit síť konečných prvků a případně ji zjemnit v oblasti otvoru tak, aby výsledky odpovídaly údajům v DIN 18008.
Výchozí konstrukci bude představovat obdélníková deska s vrtaným otvorem:
a = 300 mm
b = 600 mm
t = 10 mm
Na desce vznikají napětí maximálně 48,2 N/mm². V souladu s osvědčením [3] leží dané hodnoty v přípustném rozmezí od 46 do 52 N/mm², a proto lze model použít.
Po ověření napětí na vrtaném otvoru je v dalším kroku třeba přezkoumat model držáku.
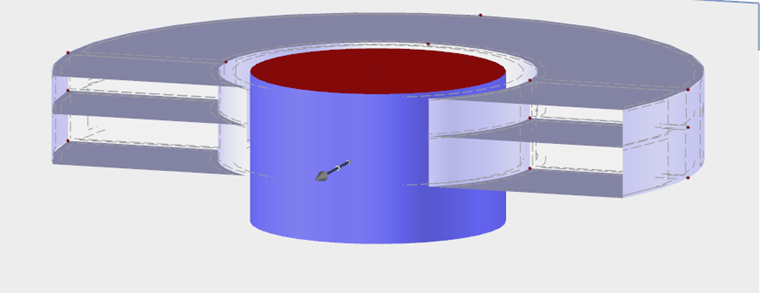
Plochy na horní i spodní straně držáku se modelují pomocí kontaktních těles, která mohou přenášet pouze tlakové síly. Tuhost tělesa se určí na základě tuhosti příslušného bodového držáku.
V našem příkladu se stanoví následující hodnoty:
Materiál na horní straně: E = 40 N/mm², G = 13,8 N/mm²
Materiál na dolní straně: E = 50 N/mm², G = 24,1 N/mm²
Pokud uvažujeme maximální dovolené zatížení FD/Z = 8,9 kN a FQ = 5,1 kN [3], dostaneme následující hodnoty tuhosti:
Tlak Z / wZ = 19 347 N/mm
Tah D / wD = 20 602 N/mm
Smyk Q / uQ = 5 247 N/mm
Jestliže hodnoty porovnáme s osvědčením [3], nacházejí se všechny výsledky v přípustném rozmezí:
15 386 N/mm ≤ cZ,D ≤ 24 372 N/mm
344 N/mm ≤ cQ
Vytvořený model tak můžeme dále použít pro výpočet.
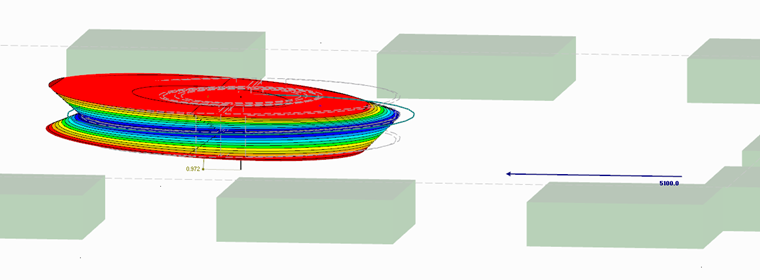
Jako poslední krok se ověří celý model. V tomto případě spojíme obě modelované dílčí konstrukce. Rozměry konstrukce, které se mají uvažovat, i požadované výsledky jsou uvedeny ve stavebním technickém osvědčení [3].
Jak dokazuje obrázek výše, stávající výsledky se velmi dobře shodují s požadovanými výsledky. Tento ověřený model konečných prvků nám dále poslouží jako základ pro vlastní statický výpočet.
Posouzení metodou konečných prvků
Posuzovat budeme stejnou konstrukci včetně zatížení jako v první části našeho příspěvku. Tím se také ukážou rozdíly při uplatnění obou metod posouzení.
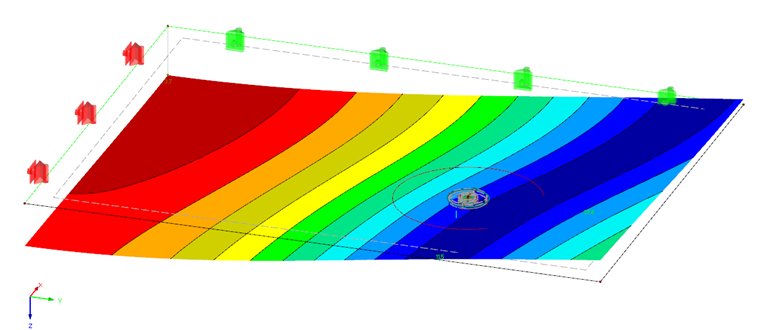
Vytvořený model konečných prvků nyní vložíme do konstrukce, kterou budeme posuzovat. Výsledná napětí použijeme pro posouzení.
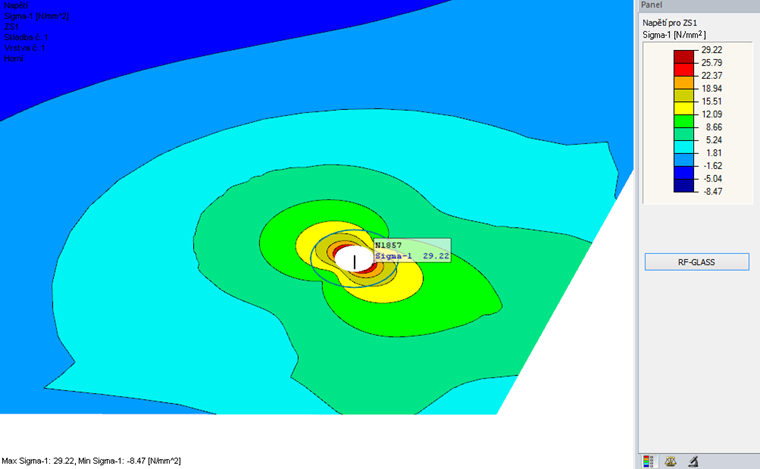
Maximální hodnota napětí v oblasti vrtaného otvoru činí σ = 29,22 N/mm². Výsledné využití je tudíž η = 29,2 / 51,3 = 0,57.
Závěr
Při porovnání obou metod výpočtu se ukazuje, že se mohou vyskytnout určité rozdíly ve vypočítaných hodnotách využití. V tomto případě je výsledkem exaktní analýzy asi o 40 % menší využití. Takový výsledek nemůžeme zobecňovat, je ovšem zřejmé, že přesná analýza metodou konečných prvků může být mnohdy výhodná.
.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)