Calculation Process
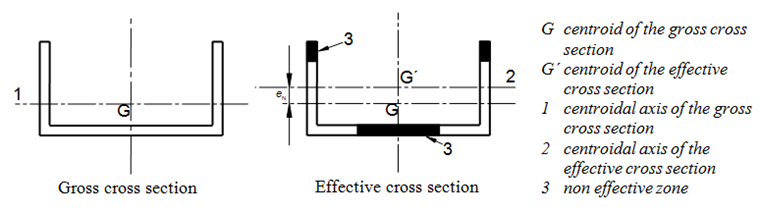
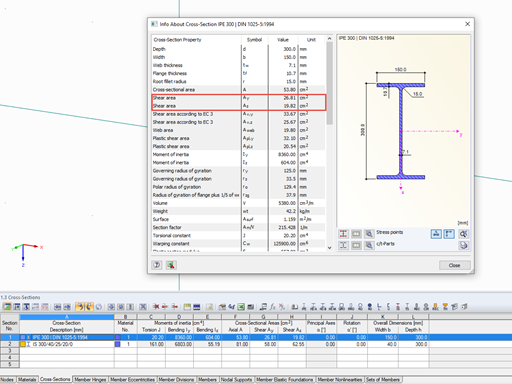
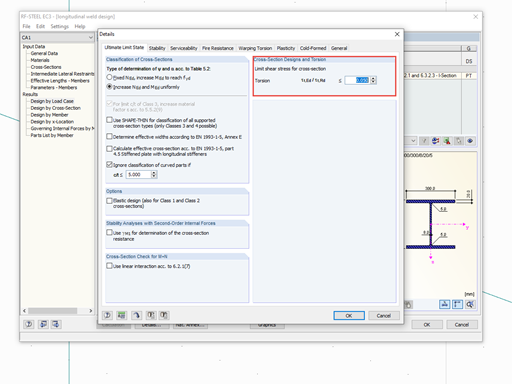
In the first calculation step, the stress distribution is determined on a gross cross-section. According to EN 1993‑1‑5, Sec. 4.4 [2], the buckling value kσ of the cross‑section parts subjected to compression can be determined using the existing stresses. The effective width beff of the cross‑section part is calculated on the basis of the slenderness ratio at buckling λp and the resulting reduction factor ρ. The resulting reduction is deducted from the entire cross-section. This gives you the result of new cross-section dimensions and properties.
At this point, the calculation is not yet complete. There is a further iteration step, where the new stress distribution with the existing internal forces is calculated on the basis of the reduced cross-section. The following must be considered:
- By reducing the cross‑section, the center of gravity is shifted. The possible acting normal forces generate an additional moment at the distance of the new center of gravity to the old one.
- The cross‑section reduction may also have an effect on the rotation of the major axes. In such cases, the deviation moment Iyz must be taken into account.
After determining the stresses, the slenderness of the cross-section parts subjected to compression is checked again. If more reductions are necessary, the iterative process continues as long as no significant cross-section modifications occur. Only then, it is possible to perform the corresponding designs of the effective cross-sections.
Conclusion
The quick determination of effective cross-sections performed initially may easily become a time-consuming calculation due to several iterations required. You can easily avoid such difficulties by using the powerful SHAPE‑THIN program as well as the add‑on modules for structural steel analysis and design.










































.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)