TS selon Quast et Quast modifié

Quast

Ce modèle utilisé pour déterminer l’efficacité du béton sur la traction entre les fissures est basé sur une courbe contrainte-déformation définie du béton dans la zone en traction (diagramme parabole-rectangle).

Les hypothèses de base de l'approche Quast peuvent être résumées comme suit :

• Contribution totale du béton à la traction jusqu’à atteindre la déformation de fissuration ε_cr ou la résistance de calcul en traction du béton f_ct,R
• Appuis de raidissement réduits du béton dans la zone en traction selon la déformation existante du béton.
• Aucune application de raidissement en traction après le début du fluage de la barre d’armature déterminante.

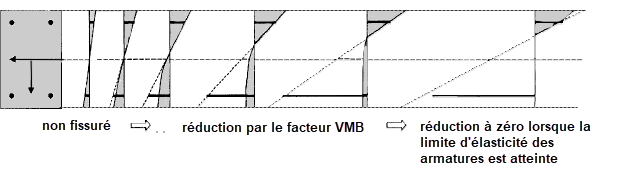
Pour résumer, cela signifie que la résistance en traction f_ct,R utilisée pour le calcul n'est pas une valeur fixe mais est relative à la déformation existante dans la fibre en acier déterminante (traction). La résistance maximale en traction f_ct,R diminue linéairement jusqu'à zéro, à partir de la déformation de fissure ε_cr définie jusqu’à atteindre la déformation d’élasticité de l’acier de béton armé dans la fibre déterminante de l’acier.
C’est réalisable par le diagramme contrainte-déformation dans la zone en traction du béton (diagramme parabole-rectangle) affiché dans l’image suivante et par la détermination d’un facteur de réduction VMB (contribution du béton).

Courbe contrainte-déformation du béton en traction avec facteur de réduction VMB = 0,4

La figure suivante affiche une vue schématique des états de contrainte pour une charge croissante due au raidissement en traction.

État de contrainte sous chargement croissant et raidissement en traction

Le diagramme contrainte-déformation dans la zone en traction peut être décrit à l’aide des équations suivantes :

• La courbure de la parabole dans la première section peut être contrôlée par l’exposant n_PR.
• L’exposant doit être ajusté de sorte que le passage de la zone de compression à la zone de traction soit réalisé avec le même module d’élasticité.

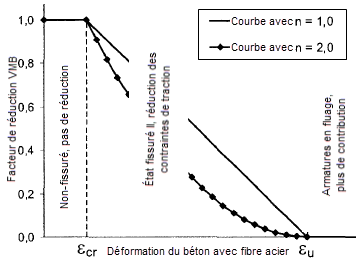
Pour déterminer le facteur de réduction VMB, la déformation au niveau de la fibre d’acier la plus tendue est utilisée. La position du point de référence est illustrée dans le graphique ci-dessous.

Détermination de la résistance en traction résiduelle pour le raidissement en traction selon Quast

Le paramètre de réduction VMB diminue avec l’augmentation de la déformation de l’acier. Le diagramme du facteur VMB (voir la figure ci-dessous) montre que le facteur VMB est réduit à zéro précisément au moment où la limite d’élasticité des armatures commence.

Facteur de réduction VMB – Raidissement en traction selon Quast

La distribution du facteur de réduction VMB à l’état II (ε > ε_cr) peut être contrôlée à l’aide de l’exposant n_VMB.

• Selon Pfeiffer [2], les valeurs n_VMB = 1 (linéaire) à n_VMB = 2 (parabole) sont des valeurs expérimentale pour les composants de structure soumis à la flexion.
• Quast [3] utilise l’exposant n_VMB = 1 (linéaire) dans son modèle, aboutissant ainsi à une bonne concordance lors du recalcul des tests de poteau.
• Selon Pfeiffer [2], il est possible de décrire les tests en traction pure avec une concordance acceptable en utilisant n_VMB = 2.

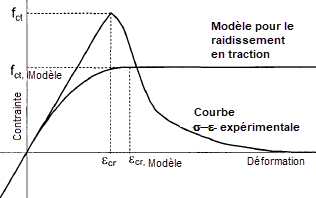
La supposition d’un diagramme rectangle-parabole pour la zone de traction du béton fissuré peut être considérée comme une aide au calcul. À première vue, il existe des différences importantes par rapport aux diagrammes contrainte-déformation déterminés expérimentalement à la face en traction du béton seul.

Raidissement en traction selon Quast - Comparaison du modèle et de l’essai en laboratoire

Les contraintes en flexion de la section en béton armé montrent que le diagramme parabole-rectangle est mieux adapté à la moyenne des déformations et des contraintes.
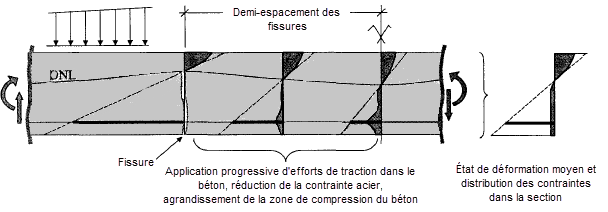
Dans une poutre en flexion, un corps en béton se forme entre deux fissures. Il s’agit d’une sorte de voile dans lequel les efforts de traction sont progressivement réintroduits par les armatures. Il en résulte une distribution très irrégulière des contraintes et des déformations. En moyenne, cependant, nous pouvons créer un niveau de déformation avec un diagramme parabole-rectangle, permettant de considérer la courbure moyenne.

État de contraintes existant pour le béton armé en flexion

Pour le modèle de Quast, les valeurs de calcul à appliquer ont été proposées comme suit :

• pour la résistance en traction f_ct,R

• pour la déformation de fissuration ε_cr,R

La valeur de calcul de la résistance en traction f_ct,R est donc inférieure à la valeur indiquée dans l’Eurocode. Cela est dû à la relation contrainte-déformation et à la détermination du facteur de réduction VMB, avec lequel la contrainte de traction présumée et l’effort de traction résultant ne sont que lentement réduits après avoir dépassé la déformation en traction. Pour une déformation de 2 ⋅ ε_cr, il y a également une contrainte de traction agissante d’environ 0,95 ⋅ f_ct,R . Ainsi, en cas de flexion, la réduction de la rigidité peut être bien prévue. Pour la traction pure, les valeurs mentionnées ci-dessus pour f_ct,R sont trop faibles. Selon Pfeiffer [2], les valeurs de l’EC 2 doivent être appliquées pour la valeur de calcul de la résistance en traction.
Les valeurs de f_ct,R = 1/20 ⋅ f_cm recommandées par Quast [3] peuvent être atteintes en appliquant 60&nsp;% des résistances en traction selon l’EC 2. La fissuration de la section est prévue trop tôt lors de l’application de f_ct,R = 0,6 ⋅ fctm. Par contre, ce calcul prend déjà en compte une réduction de la résistance en traction sous charge permanente (environ 70 %) ou une charge temporairement plus élevée (par exemple, l'application à court terme de la combinaison d’actions rare) qui résulte en une zone de traction endommagée.
Les valeurs de calcul individuelles pour la zone en traction du béton peuvent être décrites comme suit :

Approche modifiée selon Quast