Modified TS According to Quast and Quast

Quast

This model for determining the concrete's contribution to tension between the cracks is based on a defined stress-strain curve of the concrete in the tension area (parabola-rectangle diagram).

The basic assumptions of Quast's approach can be summarized as follows:

• Full contribution of the concrete in tension until the crack strain ε_cr,R or the factored concrete tensile strength f_ct,R is reached.
• Reduced stiffening contribution of the concrete in the tension zone according to the existing concrete strain
• No tension stiffening after the governing rebar has started to yield

In summary, this means that the factored tensile strength f_ct,R is not a fixed value, but refers to the existing strain in the governing steel (tension) fiber. The maximum tensile strength f_ct,R decreases linearly to zero from the defined crack strain ε_cr,R until the yield strain of the reinforcing steel in the governing steel fiber is reached (for n_VMB = 1).
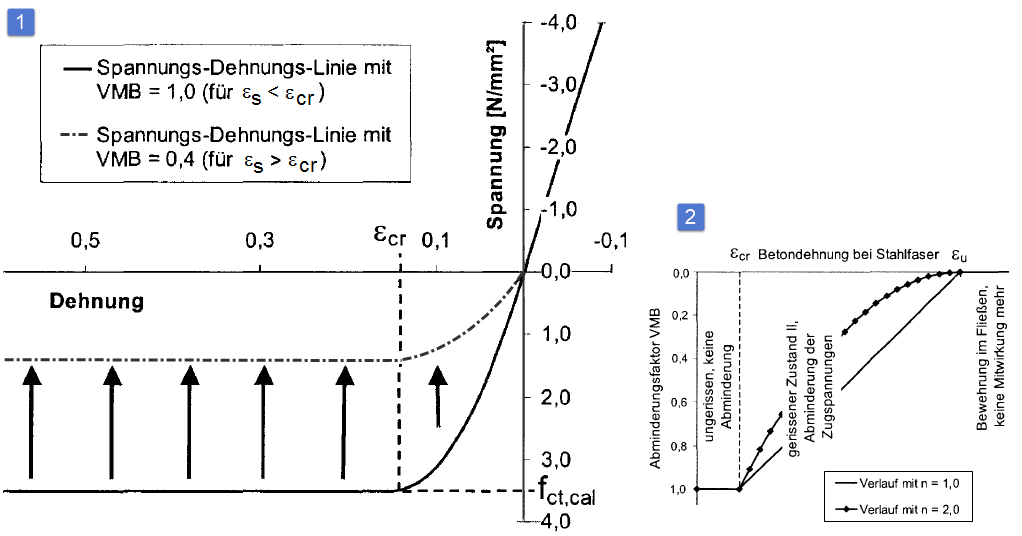
This is achieved using the stress-strain relation in the tension area of the concrete (parabola-rectangle diagram), shown in the image below, and by the determination of a reduction factor VMB (stiffening contribution of concrete).

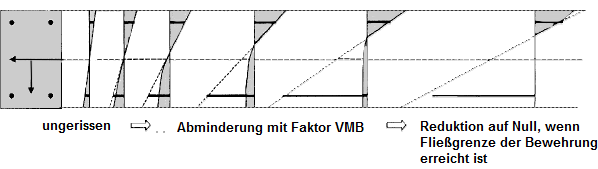
The next image shows a schematic view of stress states for increasing loading due to tension stiffening.

The stress-strain relation in the tension zone can be described with the following equations:

for 0 < ε < ε _cr,R
for ε > ε_cr,Rr

• The curvature of the parabola in the first section can be controlled by the exponent n_PR.
• The exponent should be adjusted in such a way that the transition from the compression zone to the tension zone is preferably achieved with the same modulus of elasticity.

To determine the reduction factor VMB, the strain at the most heavily tensioned steel fiber is used. The position of the reference point is illustrated in the graphic below.

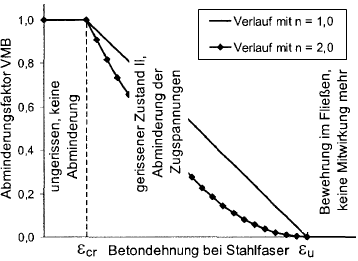
The reduction parameter VMB decreases with increasing steel strain. In the diagram for the VMB factor (see the image below), it is evident that the factor VMB is reduced to zero exactly at the point when the yielding of the reinforcement starts.

The distribution for the reduction factor VMB in state II (ε > ε_cr,R) can be controlled by means of the exponent nVMB.

• According to Pfeiffer [2], the values n_VMB = 1 (linear) to n_VMB = 2 (parabola) are experiential values for structural components subjected to bending.
• Quast [3] uses the exponent n_VMB = 1 (linear) in his model, thus achieving good concordance when recalculating column tests.
• According to Pfeiffer [2], pure tension tests with acceptable conformity can be modeled with n_VMB = 2.

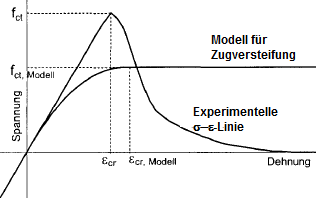
The assumption of a parabola-rectangle diagram for the cracked concrete tension zone is to be regarded as a calculation aid. At first glance, there are major differences compared to experimentally determined stress-strain curves on the tension side of the pure concrete.

The given stresses in the reinforced concrete cross-section in bending show that the parabola-rectangle diagram is indeed better suited to describe the mean of the strains and stresses.
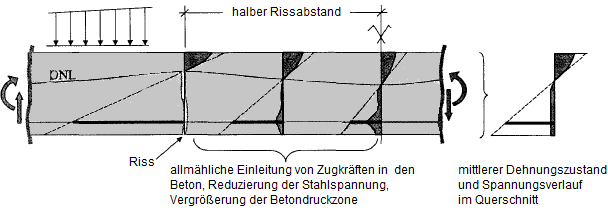
In a bending beam, a concrete body forms between two cracks. It acts as a sort of wall into which tension forces are gradually reintroduced by the reinforcement. This results in a very irregular distribution of stress and strain. On average, however, a strain level with a parabola-rectangle curve can be created, through which the mean curvature can be determined.

For the model by Quast, the calculation values to be applied were proposed as follows:

• For the tensile strength f_ct,R

• For the crack strain ε_cr,R

The calculational value for the tensile strength f_ct,R is thus smaller than specified by the Eurocode. This is due to the description of the stress-strain relation and the determination of the reduction parameter VMB, in which the assumed tension stress and the resulting tension force are only slowly reduced after exceeding the tension strain. For a strain of 2 ⋅ ε_cr, there is also an acting tension stress of about 0.95 ⋅ f_ct,R. Thus, in case of bending, the reduction of the stiffness can be predicted well. For pure tension, the above-mentioned values for fct,R are too small. According to Pfeiffer [2], the values from EC 2 should be applied for the calculation value of the tensile strength.
The values recommended by Quast [3] for f_ct,R = 1/20 ⋅ fcm can be obtained by applying 60% of the tensile strengths given in EC 2. When applying f_ct,R = 0.6 ⋅ fctm, the cross-section is predicted to crack too early. At the same time, this already takes into account a reduction in tensile strength under permanent load (about 70%) or a temporarily higher load (for example, the short-term application of the rare action combination) that leads to a damaged tension zone.
The individual calculation values for the concrete's tension zone can be described as follows:

Modified Approach According to Quast

The modified approach according to Quast uses the same calculated tensile strength f_ct,R as the approach according to Quast (see the previous section), but uses its own, simpler target curve σ̂(ε): It increases linearly from zero up to the tensile strength f_ct,R (at the strain f_{ct, R < /sub>/E, where E is the modulus of elasticity of the concrete) and remains constant thereafter. There is no parabolic component; the exponent n < /sub>sub>t < /sub>/sub> and the crack strain ε < /sub>sub>cr,R < /sub>/sub> from the Quast approach are not used. Additionally, the '''method of application''' to the concrete stress differs: * In the '''Quast''' approach, the concrete stress in the tension zone is '''set directly to the value of the target curve''' (σc = σ̂(ε), see target curve in the “Quast” section); this can result in either an increase or a decrease compared to the stress of the unmodified base material model. * In the '''modified approach''', the target curve is instead '''purely additively''' superimposed on the concrete stress σc,Main(ε) provided by the base material model (for example, damage model).}

Thus, the concrete stress can only be '''increased''', never reduced, by tension stiffening. This additive approach is numerically more robust than the forcing variant according to Quast, since it does not lead to an abrupt jump in stiffness when the base material stress already exceeds the target curve. == Implementation in Program: Local Anisotropic Tension Stiffening Extension == When using a concrete damage model, the tension stiffening is modeled using the '''local anisotropic tension stiffening extension''' [[#Ref [4]]]. In an anisotropic damage model, this method replaces the previous, globally applied approach: Instead of describing the tension zone of the cross-section once using a stress-strain diagram applicable to the entire cross-section, it superimposes a reinforcement-induced tensile stress onto the base material response of the concrete at each concrete integration point. The correction is calculated '''locally''' (at each integration point) and '''anisotropically''' (separately in both principal strain directions); the angle between the reinforcement direction and the respective principal tensile direction is explicitly taken into account. === Activation Factor === At each concrete integration point, the principal strains ε₁, ε₂, and the corresponding principal strain angle θ_p are determined; only tensile directions (ε_k > 0) are relevant for tension stiffening. Each reinforcement layer "j" contributes to the activation factor α_k of the principal direction "k" via three multiplicative subfactors: * '''g_j''' (capacity factor): Decreases with increasing reinforcement strain and becomes zero when the reinforcement reaches its yield strain. * '''a_j,k''' (angle factor): In the '''anisotropic''' damage model, 1 for parallel alignment and 0 for perpendicular alignment of the reinforcement and the principal tensile direction; for the other principal direction, the complement of these values applies. For the '''isotropic''' damage model, a different calculation applies without the use of complements; this yields the same value for both principal directions and may still differ from zero at exactly 90° under biaxial tension; see the banner “Scope of Application by Material Model” above. * '''p_j''' (position factor): 1 within the concrete cover zone of the reinforcement layer under consideration, decreasing outside this zone (strain compatibility between concrete and reinforcement). ==== Equivalent Strain ==== In the factors g_j and p_j, the strain is not treated as pure bar strain of the reinforcement or pure concrete strain, but rather as equivalent strain, which takes into account the Poisson's ratio of the concrete and the strain state at the respective location in the direction of the reinforcement: It is evaluated twice: at the location of reinforcement layer ‘'j’' (ε_eq,s,j) and in the analyzed concrete layer (ε_eq,c), in each case in the local coordinate system of the same reinforcement layer ‘'j’'. Here, ε_∥ is the strain in the direction of the reinforcement layer, and ε_⊥ is the strain perpendicular to it. The principal directions of the cross-section are not taken into account here; therefore, ε_∥ is not always the larger of the two values. This results in a reduction in the capacity of the actual opening of the concrete along the reinforcement. These equivalent strains are incorporated into the formula for the activation factor contribution. ==== Capacity Factor ==== The capacity factor decreases from 1 to 0 as the equivalent strain of the reinforcement increases from the crack strain ε _cr,R to the yield strain ε _y,j of the reinforcement; the reinforcement strain and yield strain are thus shifted by the crack strain of the concrete: If ε_y,j ≤ ε_cr,R, then g_j = 0. The exponent n_VMB (entry “Exponent of the reduction factor parabola after initial cracking”) is a material parameter that is used equally for the quast method and the modified quast method and must always be specified. The crack strain ε_cr,R is entered as “Calculated crack strain” in the Quast method (see the section [[#quast Section “Quast”]]). In the modified Quast approach, the capacity factor is calculated using ε_cr,R = 0; the displacement is omitted. The capacity factor acts as a damage value across the load increments: Once g < sub > j < /sub > has decreased, it does not increase again in subsequent load increments. The result of a multi-step calculation can therefore be smaller than the value given by the formula for the strain of the current load increment, but never larger. ==== Position Factor ==== Within the influence zone of the reinforcement location—that is, for concrete layers at a distance d_j ≤ c_j from the location—p_j = 1; the zone is symmetrical on both sides of the reinforcement. Here, d_j is the distance of the analyzed concrete layer from reinforcement layer ‘'j’', and c_j is the influence distance. The influence distance is equal to the distance from the center of the layer to the nearest cross-sectional surface, c_j = max(0, h/2 − |z_s,j|), where h is the cross-section thickness and z_s,j is the location of the reinforcement layer with respect to the center plane; this distance is determined individually for each reinforcement layer. It is not the same as the entered concrete cover: It is measured up to the center of the layer, and layers located deeper have a larger influence distance. If a layer is located at the center of the cross-section, then c_j = h/2, and p_j is 1 over the entire cross-section. Further away from the reinforcement (d < sub > j < /sub > > c < sub > j < /sub > ;), the factor is derived from the ratio of the equivalent strains at the location of the reinforcement and in the concrete layer under consideration, with a limitation to [0, 1]: This distribution is not a fixed feature of d_j/c_j: Both equivalent strains depend on the current strain state, so the shape changes with the load case. The graphic shows it for an exemplary linear strain diagram across the cross-section thickness. The position factor is calculated for every point in the cross-section and every reinforcement layer, including points on the opposite side of the cross-section. Whether tension stiffening acts at a point at all is determined independently by a separate reference strain: Tension stiffening can be active for the respective principal direction only if the reference strain is positive (tension); it is never active if the reference strain is zero or if compression is present, regardless of the value of p < sub > j < /sub>. The reference strain is derived from the strain of the base material model in the principal direction under consideration, superimposed with a component coupled via the Poisson's ratio and based on the actual principal strains. It is not the equivalent strain ε_eq,s,j or ε_eq,c and does not depend on any specific reinforcement layer. The contributions of all reinforcement layers are combined using p-norms into two factors in the principal direction ‘'k’': the geometric factor a_k and the combined capacity factor g_k. The weights of the reinforcement layers are w_j = p_j ⋅ a_j,k: The capacity factor is therefore not averaged, but combined by weighting it with the same exponent p as the geometric factor: locations with greater weight contribute significantly more, and which location is governing at a given point can therefore change between load increments. Only after the combination is there a limitation of g_k at 5% to prevent a single reinforcement layer—which is already yielding but geometrically relevant—from completely reducing the activating process of a concrete layer under minimal stress to zero. The lower limit does not affect the individual g_j nor does it apply within the p-norm. The activation factor for the principal direction ‘'k’' is derived from both factors and is subject to limitation to the interval [0, 1]: Without the lower limit and the limitation to 1, the product a_k ⋅ g_k is equal to the p-norm of the contributions Δα_j,k from the formula for the activation factor contribution. === Implementation in Quast and Modified Quast === The target stress in the principal direction ‘‘k’’ results in: There are two options for the underlying target stress curve σ̂(ε), the theoretical background of which is described in the preceding sections. Neither curve includes any reduction due to the capacity factor; this factor acts exclusively through g_j: ==== Implementation for Quast ==== When fully activated, the implementation corresponds to the direct specification of the target curve for the concrete stress described in the “Quast” section. In general, the concrete stress in the principal direction ‘'k’' is given by the weighted superposition of the target stress and the stress σ_c,Basis of the base material model: When a_k = 1 and g_k = 1, this corresponds to the direct specification of the target curve; when a_k = 0, the stress of the base material model remains unchanged. ==== Implementation for Quast Modified ==== When fully activated, the implementation corresponds to the purely additive correction described in the section “Modified Approach According to Quast”. When partially activated, the correction is incorporated into the concrete stress on a proportional basis, according to the partial factors of the activating factor. === Limitations of Method ===