TS zmodyfikowany zgodnie z Quast i Quast

Quast

Model ten, używany do określania efektywności betonu przy rozciąganiu między rysami, oparty jest na zdefiniowanej krzywej naprężenie-odkształcenie betonu w strefie rozciąganej (wykres paraboli-prostokąt).

Podstawowe założenia podejścia Quasta'sa można podsumować następująco:

• pełny udział betonu na rozciąganie aż do osiągnięcia odkształcenia rysującego ε_cr lub obliczeniowej wytrzymałości betonu na rozciąganie f_ct,R
• Zredukowany udział usztywnienia betonu w strefie rozciąganej zgodnie z istniejącym odkształceniem betonu.
• Nie stosuje się usztywnienia rozciąganego po tym, jak decydujący pręt zbrojeniowy zacznie uplastyczniać.

Podsumowując, oznacza to, że wytrzymałość na rozciąganie f_ct,R zastosowana w obliczeniach nie jest wartością stałą, ale odnosi się do istniejącego odkształcenia w decydującym włóknie stalowym (rozciąganie). Maksymalna wytrzymałość na rozciąganie f_ct,R maleje liniowo do zera, począwszy od zdefiniowanego odkształcenia rysunkowego ε_cr, aż do osiągnięcia granicy plastyczności stali zbrojeniowej w głównym włóknie stalowym.
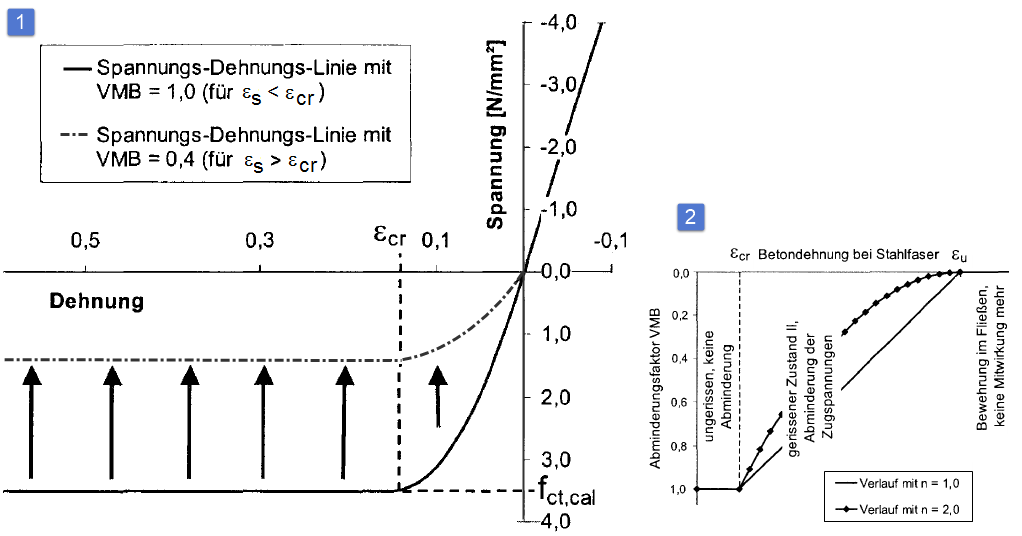
Można to osiągnąć za pomocą wykresu naprężenie-odkształcenie w obszarze rozciągania betonu (wykres parabola-prostokąt) pokazanego na poniższym rysunku oraz poprzez określenie współczynnika redukcyjnego VMB (udział betonu usztywniający).

Krzywa naprężenie-odkształcenie betonu w strefie rozciągania ze współczynnikiem redukcyjnym VMB = 0,4

Następny rysunek przedstawia schematyczny widok stanów naprężeń dla rosnących obciążeń spowodowanych usztywnieniem na rozciąganie.

Stan naprężenia dla rosnącego obciążenia ze sztywnieniem przy rozciąganiu

Wykres naprężenie-odkształcenie w obszarze rozciągania można opisać za pomocą następujących równań:

• Zakrzywienie paraboli w pierwszym przekroju może być kontrolowane za pomocą wykładnika n_PR.
• Wykładnik należy dostosować w taki sposób, aby przejście ze strefy ściskania do strefy rozciągania odbywało się korzystnie z takim samym modułem sprężystości.

Do wyznaczenia współczynnika redukcyjnego VMB wykorzystywane jest odkształcenie w najbardziej rozciąganym włóknie stalowym. Położenie punktu odniesienia pokazano na poniższym rysunku.

Określanie wytrzymałości resztkowej na rozciąganie dla usztywnienia rozciągającego zgodnie z Quastem

Parametr redukcyjny VMB zmniejsza się wraz ze wzrostem odkształcenia stali. Z wykresu współczynnika VMB (patrz rysunek poniżej) widać, że współczynnik VMB zostaje zredukowany do zera dokładnie w punkcie, w którym rozpoczyna się uplastycznienie zbrojenia.

Współczynnik VMB – Ujęcie sztywności na rozciąganie wg Quasta

Rozkład współczynnika redukcyjnego VMB w stanie II (ε > ε_cr ) można kontrolować za pomocą wykładnika n_VMB.

• Według Pfeiffera[2] wartości n_VMB = 1 (liniowo) do n_VMB = 2 (parabola) są wartościami empirycznymi dla elementów konstrukcyjnych poddanych zginaniu.
• Quast [3] wykorzystuje w swoim modelu wykładnik n_VMB = 1 (liniowy), osiąga w ten sposób dobrą zgodność podczas ponownego obliczania testów słupów.
• Według Pfeiffera [2], można opisać czystą próbę rozciągania z akceptowalną zgodnością za pomocą n_VMB = 2.

Jako pomoc w obliczeniach można wykorzystać wykres parabola-prostokąt dla strefy rozciąganej betonu zarysowanego. Na pierwszy rzut oka istnieją znaczne różnice w porównaniu z wyznaczonymi eksperymentalnie wykresami naprężenie-odkształcenie po stronie rozciągania czystego betonu.

Początki uplastycznienia według Quasta: porównanie modelu i testu laboratoryjnego

Podane naprężenia w zginanym przekroju żelbetowym pokazują, że wykres paraboli-prostokątny rzeczywiście lepiej nadaje się do opisania średniej odkształceń i naprężeń.
W belce zginanej pomiędzy dwiema rysami powstaje bryła z betonu. Zachowuje się ona jak ściana, w której siły rozciągające są stopniowo przywracane przez zbrojenie. Skutkuje to bardzo nieregularnym rozkładem naprężeń i odkształceń. Średnio możemy jednak utworzyć płaszczyznę odkształcenia o rozkładzie parabola-prostokąt, dzięki której można uwzględnić średnią krzywiznę.

Istniejący stan naprężenia dla betonu zbrojonego przy zginaniu

W przypadku modelu firmy Quast zaproponowano następujące wartości obliczeniowe

• dla wytrzymałości na rozciąganie f_ct,R

• dla odkształcenia rysującego ε_cr,R

Wartość obliczeniowa wytrzymałości na rozciąganie f_ct,R jest zatem mniejsza niż wartość określona w Eurokodzie. Wynika to z opisu zależności naprężenie-odkształcenie oraz wyznaczenia parametru redukcyjnego VMB, w którym założone naprężenie rozciągające i wynikająca z niego siła rozciągająca są jedynie powoli redukowane po przekroczeniu odkształcenia przy rozciąganiu. Dla odkształcenia 2 ⋅ ε_cr również występuje naprężenie rozciągające wynoszące około 0,95 ⋅ f_{ct, R} . Dzięki temu w przypadku zginania można dobrze przewidzieć redukcję sztywności. W przypadku czystego rozciągania powyższe wartości f_ct,R są zbyt małe. Zgodnie z Pfeiffer[2], do wartości obliczeniowej wytrzymałości na rozciąganie należy zastosować wartości z EC 2.
Wartości dla f_ct,R = 1/20 ⋅ f_cm zalecane przez Quast [3] można osiągnąć, stosując 60 % wytrzymałości na rozciąganie podanych w EC 2. Z jednej strony , zarysowanie przekroju jest spodziewane zbyt wcześnie przy zastosowaniu f_{ct, R} = 0,6 ⋅ fctm. Z drugiej strony, uwzględnia to już zmniejszenie wytrzymałości na rozciąganie pod obciążeniem stałym (około 70 %) lub chwilowo większe obciążenie (np. krótkotrwałe zastosowanie rzadkiej kombinacji oddziaływań), które skutkuje uszkodzeniem strefy rozciąganej.
Poszczególne wartości obliczeniowe dla strefy rozciąganej betonu's można opisać w następujący sposób:

Zmodyfikowane podejście według Quast