Sensitivity Coefficient θ
The sensitivity coefficient θ is defined as follows [1]:
|
θ |
Interstory drift sensitivity coefficient |
|
Ptot |
Total gravity load at and above the story considered in the seismic design situation |
|
dr |
Design interstory drift, evaluated as the difference of the average lateral displacements ds at the top and bottom of the story under consideration; for this, the displacement is determined by using the linear design response spectrum with q = 1.0 |
|
Vtot |
Total seismic story shear determined by using the linear design response spectrum |
|
h |
Story height |
The second-order effects may be taken into account approximately by a factor equal to 1 / (1 − θ), if 0.1 < θ ≤ 0.2.
For θ > 0.2, it is necessary to consider the geometric stiffness matrix when calculating eigenvalues and multi-modal response spectrum analysis.
The sensitivity factor can also be calculated in RFEM 6 and RSTAB 9. Find more information in this Knowledge Base article: KB | Determination of Sensitivity Coefficient to Investigate Need for Second-Order Analysis in Dynamic Analyses .
Geometric Stiffness Matrix
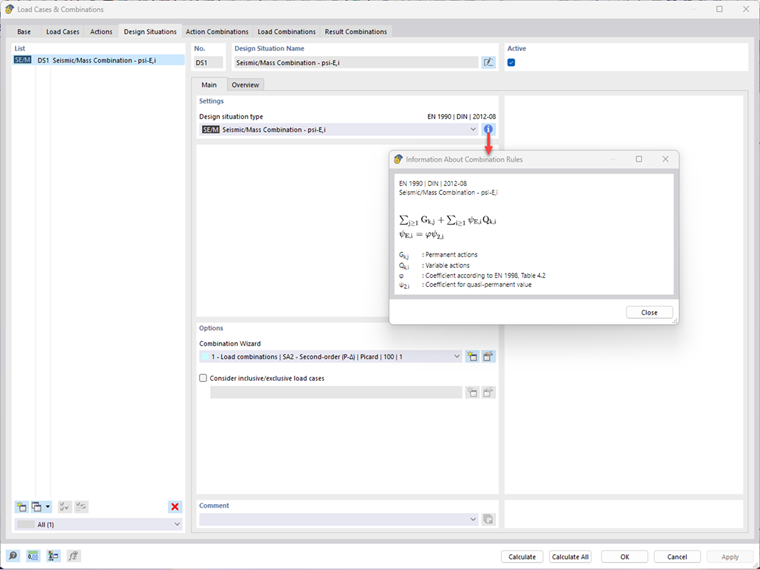
For dynamic analyses, the iterative calculations for the nonlinear determination of second-order theory are not suitable. The problem can be linearized, and it is sufficient to use the geometric stiffness matrix based on axial loads to consider the second-order theory. For this, it is assumed that the vertical loads do not change due to horizontal effects, and the deformations are small compared to the building dimensions [2]. The loads to be considered should correspond to those for the seismic design situations in accordance with EN 1990, Section 6.4.3.4 [3]:
|
Ed |
Bemessungswert der Einwirkungen |
|
Gk,j |
charakteristischer Wert einer ständigen Einwirkung j |
|
Qk,i |
charakteristischer Wert einer veränderlichen Einwirkung i |
|
Ψ2,i |
Beiwert für quasi-ständige Werte der veränderlichen Einwirkungen i |
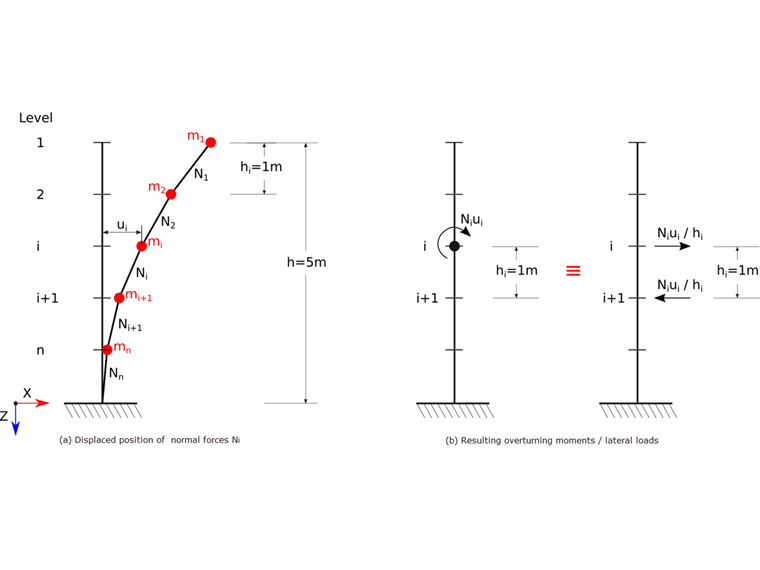
Axial tensile forces increase the stiffness, for example, in a prestressed cable. Compression forces reduce the stiffness and can lead to a singularity in the stiffness matrix. The geometric stiffness Kg is not dependent on the mechanical properties of the structure, but only on the member length L and axial force N. To illustrate the basic problem, a simple example of a cantilever is displayed in Image 01. The individual mass points of the cantilever represent the individual stories of a building. The building is subjected to a dynamic analysis considering the second-order theory. The axial forces Ni on the individual stories i = 1…n result from the vertical forces in the seismic design situation. The storey height is defined by hi.
The geometric stiffness matrix Kg can be derived from the static equilibrium conditions:
For the purpose of simplification, only the degrees of freedom of the horizontal displacement are displayed here. The derivation shown is based on the overturning moment approach due to the linear displacement application. This is a simplification for the bending element, and an accurate assumption for the truss element. More precise determination of the geometric stiffness matrix for bending beams can be obtained by using the cubic displacement approach or the analytical solution of the differential equation of the bending line. More information and derivations are provided by Werkle [4]. The geometric stiffness matrix Kg is added to the system stiffness matrix K, and thus the modified stiffness matrix Kmod is obtained:
Kmod = K + Kg
In the case of compression normal forces, this consequently leads to stiffness reduction.
Example: Natural Frequencies and Multi-Modal Response Spectrum Analysis Considering Second-Order Theory
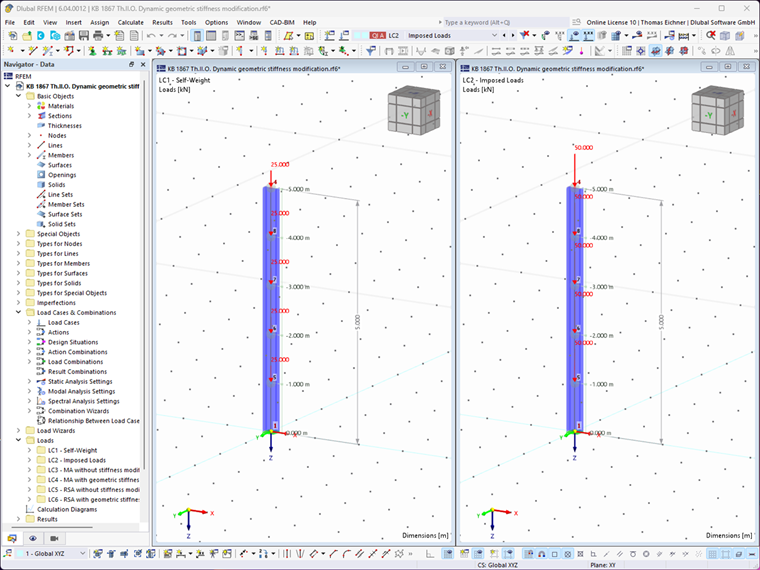
The following shows how the geometric stiffness matrix can be considered in RFEM 6 and RSTAB 9. The cantilever shown in Image 01 is used as an example. The cantilever consists of five concentrated mass points. Here, 4,000 kg act in the global X-direction in each case.
The cross‑section is IPE 300 made of S 235 material with Iy = 8,356 ∙ 10-5 m4 and E = 2.1 ∙ 1011 N/m². To be able to consider the geometric stiffness matrix in the dynamic analysis, a design situation of the seismic/mass combination is initially defined in the RFEM main program. Thus, the load combination (CO1) used subsequently is automatically created by the combinatorics integrated in the program.
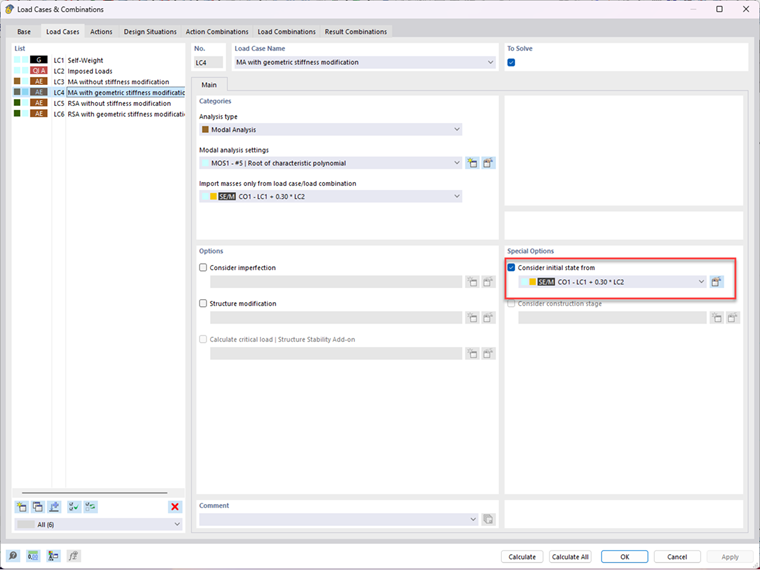
The Modal Analysis add-on allows you to determine mode shapes and effective modal masses of a structure. It is possible to select the initial states in order to consider the stiffness modifications based on load cases and load combinations.
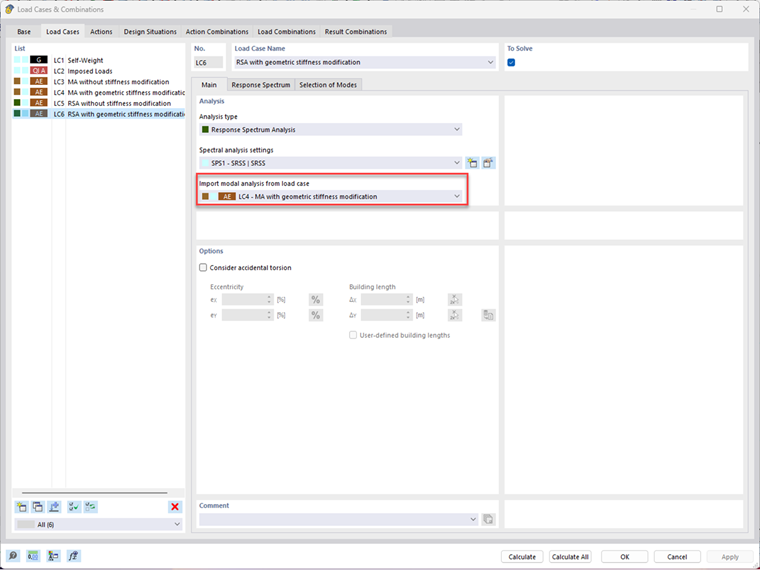
Two modal analysis load cases are defined. In LC4, CO1 is imported in order to consider the geometric stiffness matrix and thus the second-order analysis. For comparison, LC3 is defined, which does not include any stiffness modifications.
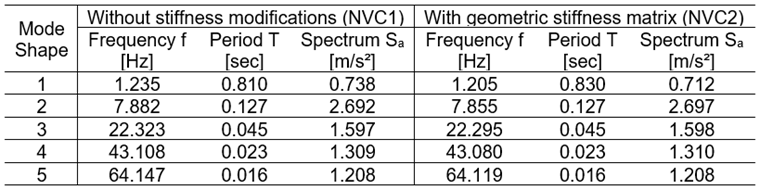
The following table includes the determined natural frequencies f [Hz], natural periods T [sec], and the acceleration values Sa [m/s²] based on the response spectrum, with and without the geometric stiffness matrix Kg resulting from the axial forces of CO1.
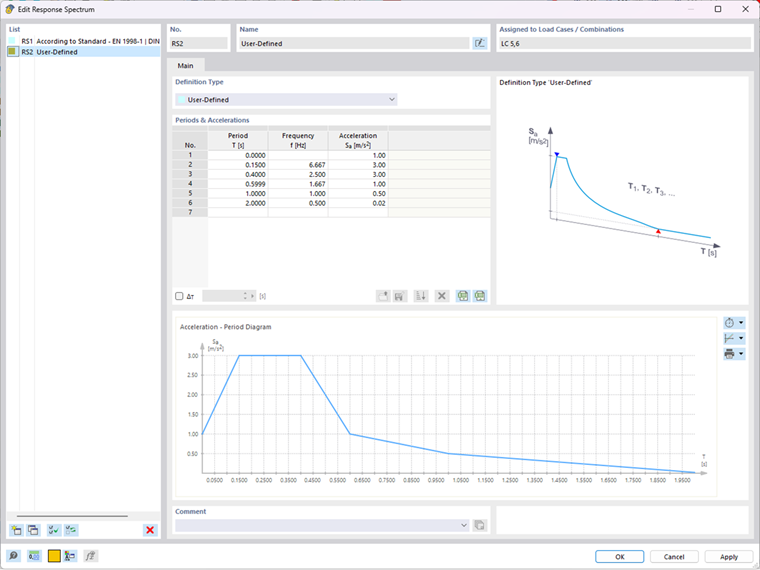
The multi-modal response spectrum analysis uses natural frequencies to determine the acceleration values from the defined response spectrum. Based on these acceleration values, the internal forces and moments of the response spectrum analysis are determined. The graphic display of a user‑defined response spectrum is shown in Image 06, and the acceleration values Sa [m/s²] determined from the response spectrum for each eigenvalue are listed in the table above.
In order to ensure the correct assignment of the modified frequencies, the desired modal analysis must be used as a basis when creating a response spectrum load case.
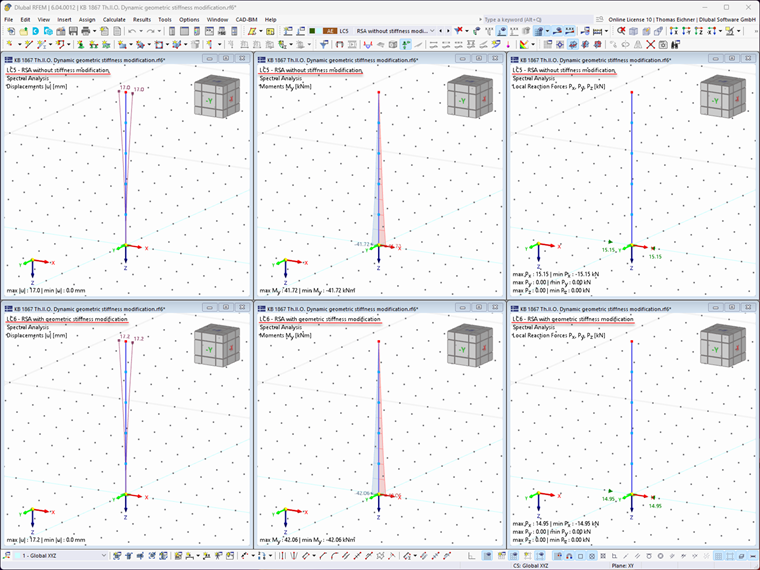
In the case of compression axial forces, the consideration of the geometric stiffness matrix leads to the reduction of the natural frequency, and can cause lower acceleration values Sa, as in our example. Sole modification of the natural frequencies is not enough to consider the second-order theory. In fact, this may actually lead to smaller results, which can be thus incorrect. It is very important to also use the modified stiffness matrix for the determination of internal forces and deformations. In the response spectrum analysis, the modified stiffness from the modal analysis is automatically used for determining the results of the response spectrum analysis. The deformations, internal forces and moments, and support reactions determined in the response spectrum analysis, with and without the geometric stiffness matrix, are shown in Image 08.
The consideration of the geometric stiffness matrix leads to larger deformations and internal forces. However, the resulting support loads are slightly smaller when considering the geometric stiffness matrix.