Members
Internally, the cross-section is meshed for the nonlinear calculation method, whereby different materials are assigned to the individual elements (reinforcement and concrete) and the individual concrete elements can assume different stiffnesses during the calculation (cracking of the concrete).
The FE mesh for the nonlinear analysis can be viewed in the cross-section dialog and its mesh fineness can be controlled. The following image shows the corresponding input dialog box.
Surfaces
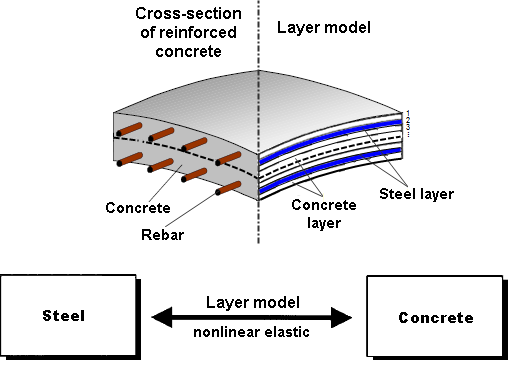
Internally, the FE element is modeled in layers for the nonlinear calculation method, with different materials being assigned to the individual layers (reinforcement and concrete) and the individual concrete layers being able to assume different stiffnesses during the calculation (cracking of the concrete).
Integration Methods
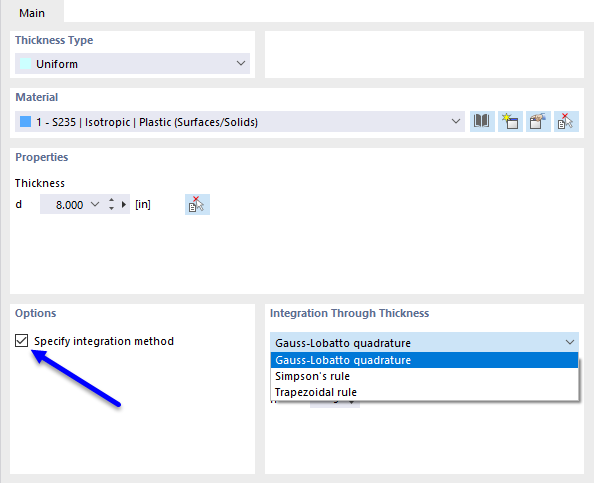
The default integration method for surfaces in RFEM is a Gauss-Lobatto quadrature with nine integration points. This default setting is sufficient for most cases.
In order to accurately model nonlinear stress-strain curves, it may be useful to increase the number of integration points. Therefore, when using nonlinear material, it is possible to define the number of integration points in each layer between three and 99 user-defined points.
However, please note that a higher number of integration points results in a longer calculation time.
The following three different integration methods are available for selection.
- Gauss-Lobatto quadrature
- Simpson's rule
- Trapezoidal rule
A more detailed description of the integration methods can be found in the manual for multilayer surfaces in the following chapter: Theory of Integration Methods.
The integration method can be defined in the thickness of the surface. The following image shows the corresponding input dialog box.
An overview of the methods based on an example is provided in the technical article Influence of Various Integration Methods on Calculation of Steel Fiber-Reinforced Concrete Slab .