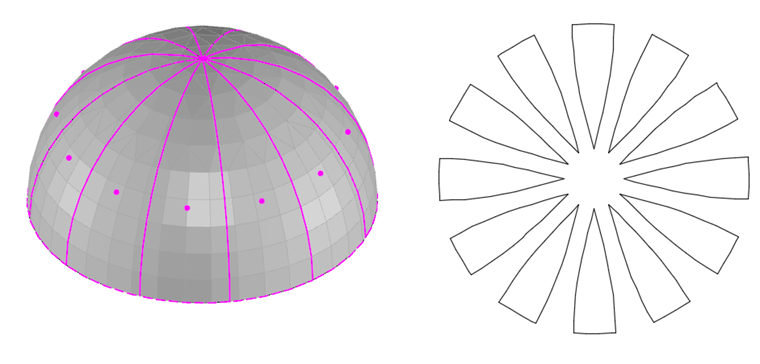
Kromě vývoje tvarů je klíčovým procesem výroba a příprava konstrukčních dílců, které se mají na staveništi montovat. V tomto případě se inženýr stává krejčím. Skvělým úkolem je vytvořit dvojitou zakřivenou membránu z mnoha malých rovinných řezných vzorů jako celku, která je vystavena danému předpětí. Obtížnost tohoto úkolu se vyjasní, pokud se pokusíme zpracovat napůl pomeranč v imaginárním modelu. Vzhledem k radiálnímu a tangenciálnímu zakřivení membránového pláště nemůže být polovina oranžová sestavena z jedné rovinné části. Rozložit ho lze pouze na několik rovinných částí.
Kromě vývoje vlastního střihového vzoru je tento rozklad velmi náročný. V sestavě by měly být řezné linie zvoleny tak, aby každá část měla ve 3D geometrii co nejvíce homogenní stav předpětí na ploše, a tím se zabrání nerovnoměrnému přídavku na protažení během procesu narovnání. Čím menší je dílčí jednotka, tím rovnoměrnější jsou rozložení předpětí a poměrné prodloužení. Tento postup vyžaduje volné nastavení řezných linií pro dílčí jednotky nezávisle na počátečním zadání a globální membránové geometrii. Při umisťování linií řezu pro dílčí jednotky je třeba zohlednit následující hlediska:
- Homogenní podmínka předpětí v 3D geometrii
- Rovnoměrné prodloužení při procesu narovnání
- Mezní šířka role materiálu
- Materiálová ortotropie
- Sledování svaru
- Architektonický návrh
- Poškození polotovaru v důsledku příliš velkých segmentů
- Montáž dřevěné konstrukce
Po narovnání se pak vytvoří pro 3D segmentovaný 3D díl nutný díl. Při procesu narovnání je třeba zohlednit následující aspekty:
- Materiálová ortotropie
- Kompenzace/relaxace na ploše a na okrajích
- Přípustné hodnoty na okrajích
- Stejné mezní délky mezi sousedními prvky
V praxi se oba pracovní kroky, kterými je definování dráhy řezu, a následné narovnání dílčích ploch, označují jako řezání.
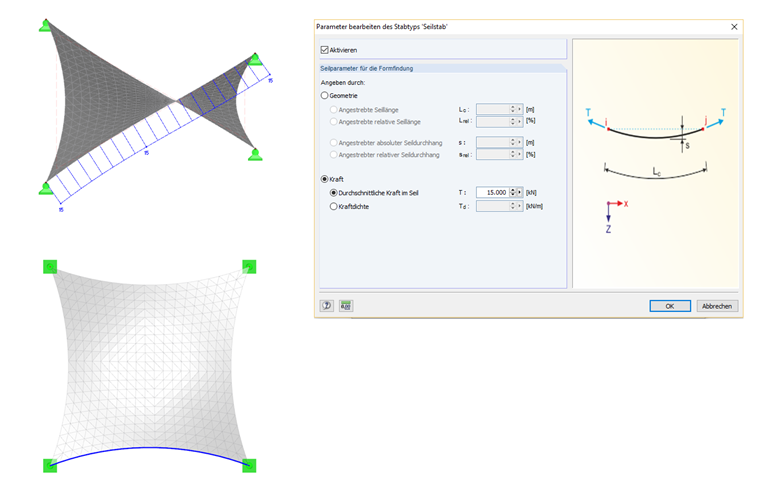
Kromě vývoje střihových vzorů u membrán se provádí i montáž lanových prvků. Výše uvedený proces form-findingu hledá takovou geometrii, která nastaví dané povrchové napětí membrány a danou lanovou sílu nebo výslednou sílu daných lanoví do rovnováhy s okrajovými podmínkami. Nakonec tento algoritmus nabízí novou geometrii s aktivními silami.
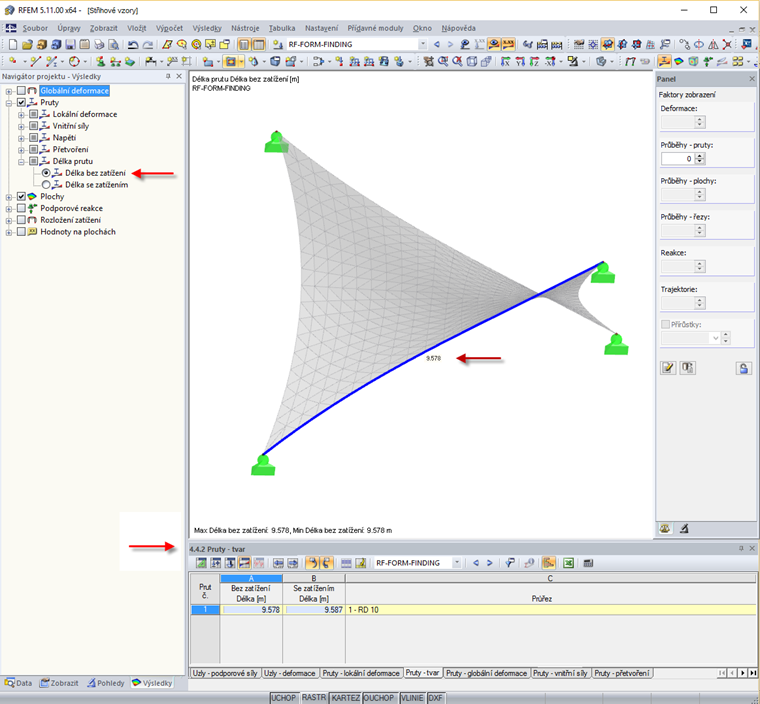
Proto délku lana pro výrobu nelze proto odvodit z čisté geometrie nalezeného tvaru, ale vychází z geometrie nalezeného tvaru snížené o prodloužení lana v důsledku působícího předpětí.
kde
A ... průřezová plocha
E ... modul pružnosti
N ... síla lana