Structure Modeling
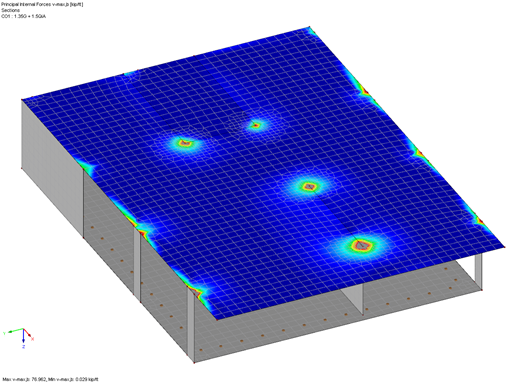
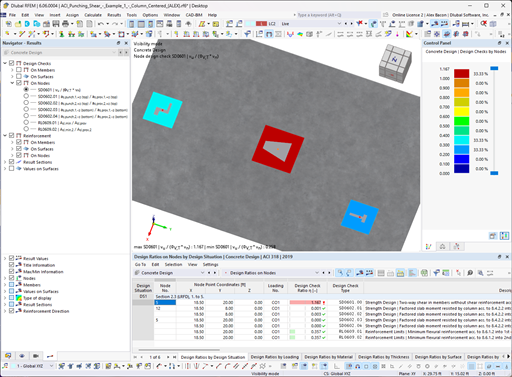
RFEM 5 allows you to perform the punching shear design for both 2D slab and 3D structures. The RF-PUNCH Pro add-on module detects the locations of punching shear automatically and recommends them for the design. An integrated filter for finding the nodes of punching shear can be set individually. In this way, you can easily sort the design checks, for example by planes., an outline of the evidence, for example in order to levels very easily possible.
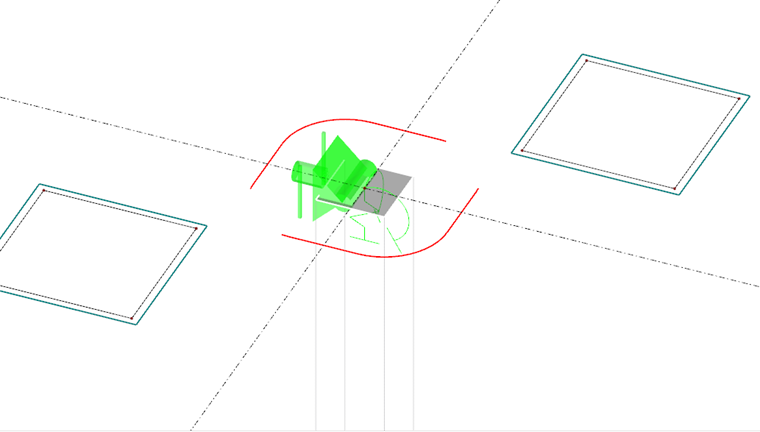
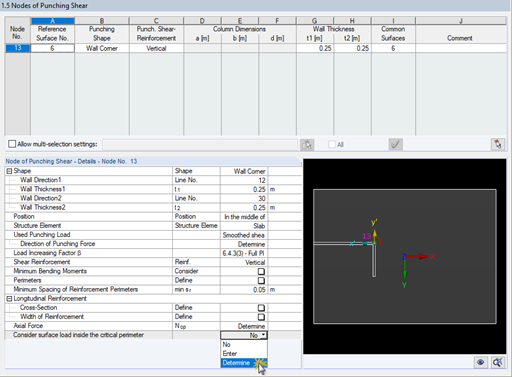
RF-PUNCH Pro automatically recognizes the type of punching node (single columns, wall ends, or corners), as well as the punching node area (inner, edge, or corner columns) from the RFEM model.
Critical Perimeter
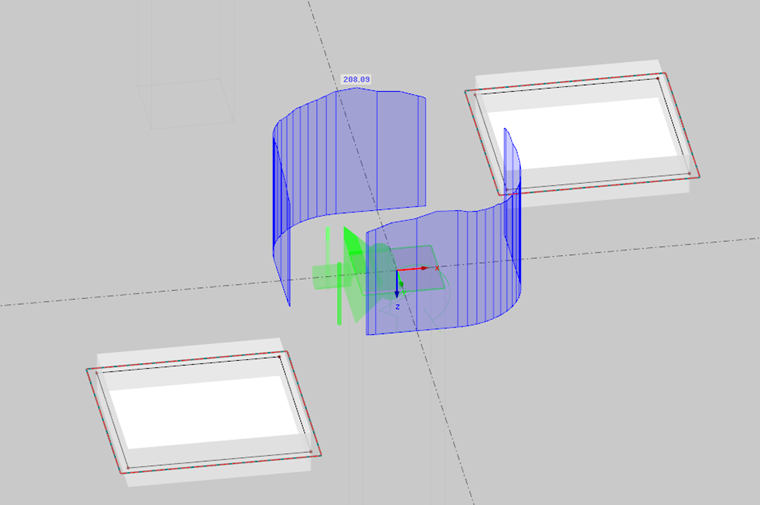
The punching shear is performed in the basic control perimeter. According to Sect. 6.4.2 of EC 2 [1], the control perimeter for slabs is located at a distance of 2d (d = the effective depth of the slab) from the load surface. Determination of the control perimeter geometry requires the consideration of column dimensions as well as slab openings up to the distance of 6d of the load surface. RF-PUNCH Pro automatically recognizes the openings modeled during the FEM analysis. In addition, you can also define smaller openings in the module, which are negligible in the structural FEM calculation, for example. These can be considered when determining the basic control perimeter. The control perimeter geometry is displayed in the input windows of the add-on module even before you start the calculation.
In the case of floor slabs or foundations, the critical perimeter is usually at a distance of 2d from the column edge. According to 6.4.4 (2) [1], the determination of the control perimeter requires an iterative calculation. The German National Annex [2] NCI to 6.4.4 (2) allows a simplified calculation for floor slabs and slender foundations with λ = aλ / d > 2 (where aλ = foundation cantilever). In this case, the control perimeter can be set at a distance of 1d. Generally, RF-PUNCH Pro performs an iterative calculation to find the control perimeter of foundations or floor slabs.
Related Shear Force vEd
The design shear force related to the control perimeter is calculated according to Eq. 6.38, EC 2 [1]:
where
u1 = the circumference of the control perimeter
d = the mean effective depth of the slab
β = the load increment factor for considering the asymmetrical distribution of shear force in the control perimeter
VEd = the design value of the punching load
In order to consider the uneven rotational symmetric load, the punching load VEd is increased by the load increment factor β. For rigidly fixed structures where the adjacent spans do not differ in length by more than 25%, you may use the following values β in accordance with EN 1992‑1‑1, Figure 6.21N [1]:
β = 1.15 for internal columns
β = 1.4 for edge columns
β = 1.5 for corner columns
The German Annex [2], Figure 6.21N, complements the β factors with β = 1.35 for wall corners and β = 1.2 for wall ends, and specifies the recommended value for internal columns as β = 1.10.
A general method for determining the load increment factor β is described in Eurocode 2 [1], Sect. 6.4.3 (3). Here, the factor β is determined assuming the fully plastic shear stress distribution in the control perimeter. In accordance with EN 1992‑1‑1 [1], Eq. (6.39), you obtain:
where
k = the coefficient depending on the column dimensions; see Table 6.1 [1]
MEd = the moment around the centroidal axis of the control perimeter
W1 = the basic control perimeter modulus
While Expression (6.39) of EN 1992‑1‑1 [1] specifies the calculation of β for uniaxial load eccentricity only, the German Annex [2] provides the expanded Expression (NA.6.39.1) for considering biaxial load eccentricity:
RF-PUNCH Pro includes both options for calculating β mentioned above. The standard method is to select the model considering the fully plastic shear stress distribution.
RF-PUNCH Pro takes the design value of shear force VEd directly from the FEM calculation to perform the punching shear design. In the case of the punching shear design for columns, nodal supports, and concentrated loads, you can determine the shear force on the basis of the column axial force, support force, or the load value of the acting concentrated force.
In addition, RF-PUNCH Pro allows you to create the control perimeter on an FEM model and determine the acting shear force VEd there. To do this, there are the following two options:
- The existing shear forces in the control perimeter are integrated or smoothed by the same control perimeter. The resulting design shear force VEd must then be multiplied by the load increment factor β (see Eq. 6.38 [1]). If the factor β is determined using the fully plastic shear distribution model, both bending moments MEd,x and MEd,y are also determined by integrating the slab internal forces in the control perimeter set on the slab.
- The maximum value of the existing shear force in the control perimeter is used for the punching shear design. This method takes into account the effect of the uneven rotational symmetric load by using the maximum value. Therefore, an additional increment of the shear force by the factor β can be omitted.
Although the utilization of the maximum shear force value in the control perimeter is the most accurate method for determining the design value of the punching load, it is also the method most susceptible to the singularity effects. In particular, you should pay attention to sufficient refinement of the FE mesh in the punching shear areas when taking the shear forces directly from the control perimeter in the FEM calculation. It is recommended to arrange at least two or three elements between the punching nodes and the control perimeter by using the FE mesh refinement.
In the case of foundations and floor slabs, you can reduce VEd by the soil pressure within the iteratively determined control perimeter; see 6.4.2 (2) [1]. If you create the basic control perimeter by 1d for slender foundations in accordance with the simplified method of German Annex [2], you can apply only 50% of the soil pressure. Both design forms can be selected in RF-PUNCH Pro.
Design Form
Before the punching shear design, the program checks whether the design can be performed without punching reinforcement.
Punching Shear Resistance Without Punching Shear Reinforcement
The punching shear resistance without shear reinforcement vRd,c has to be determined according to 6.4.4 (1), EN 1992‑1‑1 [1] as follows:
vRD,c = CRD,c ∙ k ∙ (100 ∙ ρl ∙ fck)1/3 + k1 ∙ σcp ≥ (vmin + k1 ∙ σcp)
where
CRd,c = 0.18/γc for flat slabs
CRd,c = 0.15/γc for floor slabs/foundations
k = 1 + √(200/d)
ρl,x/y = Asl,x/y / (bw · dx/y)
ρl = √(ρl,x ∙ ρl,y) ≤ 0.02
Asl = area of tension reinforcement
k1 = 0.1
σcp = the normal stress in control perimeter
vmin = 0.035 · k3/2 · fck1/2
In the German Annex [2], the parameters mentioned above are modified as follows:
CRd,c = 0.18/γc for flat slabs
CRd,c = 0.18/γc ∙ (0.1 ∙ u0 / d + 0.6) in the case of internal columns of flat slabs with u0 / d < 4
CRd,c = 0.15/γc for floor slabs/foundations
ρl = √(ρl,x ∙ ρl,y) ≤ min [0.02;0.5fcd/fyd]
vmin = (0.00525/γc) ∙ k3/2 ∙ fck1/2 for d ≤ 600 mm
vmin = (0.00375/γc) · k3/2 · fck1/2 for d > 800 mm
The punching shear design is fulfilled without additional punching reinforcement if vEd ≤ vRd,c. Due to the structurally difficult design of shear reinforcement, you can usually try to avoid using the punching reinforcement and instead, apply the maximum allowable longitudinal reinforcement ratio ρl for this purpose. RF-PUNCH Pro determines the required longitudinal reinforcement ratio in order to avoid the punching shear reinforcement. However, it is also possible to define the existing longitudinal reinforcement for the calculation of VRd,c manually.
Maximum Punching Shear Resistance vRd, max
If the punching shear design is impossible without punching reinforcement, the maximum punching shear resistance vRd,max is calculated in the next step.
According to 6.4.5 (3) of EN 1992‑1‑1 [1], the maximum punching shear resistance is performed on a column periphery. The considered periphery length u0 encloses the basic control perimeter and can be determined directly on the load surface. The maximum punching shear resistance on the column periphery vRd,max is determined according to 6.4.5. (3), EN 1992‑1‑1 [1], as follows:
vRd,max = 0.4 · ν · fcd
where ν = 0.6 · (1 - fck/250) (fck in [N/mm²])
The acting design shear force on the column periphery results from:
vEd,u0 = β · VEd / (u0 · d)
The design is fulfilled if vEd,u0 ≤ vRd,max.
In the German National Annex [2], the design of the maximum punching shear resistance is not performed on the column periphery, but in the basic control perimeter u1 according to Expression NA6.53.1 as follows:
vEd,u1 ≤ vRd,max = 1.4 · vRd,c,u1
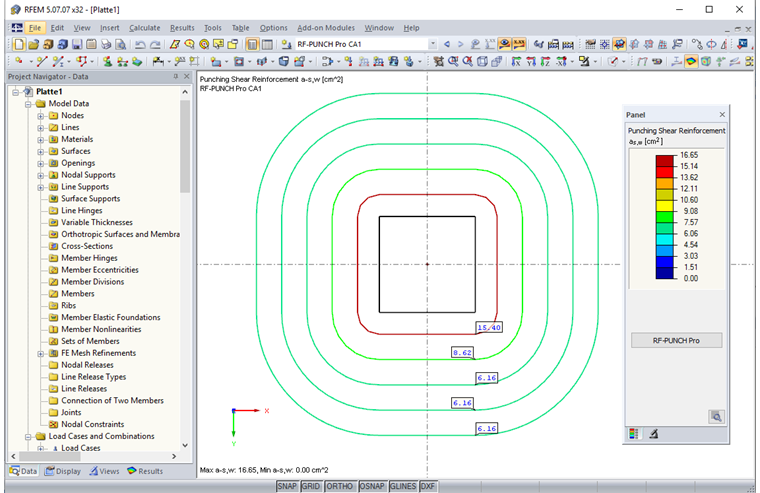
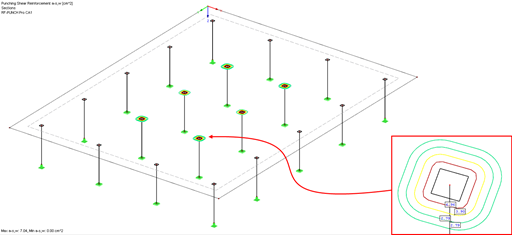
Punching Shear Resistance with Punching Shear Reinforcement
If the design of vRd,max has been performed successfully, the required punching shear reinforcement is determined in the next step. The required punching shear reinforcement is calculated according to the adjusted Expression 6.52 of EN 1992‑1‑1 [1]. The required reinforcement Asw results from the following equation:
where
vRd,c = the design shear resistance without punching shear reinforcement
d = the mean of the effective depths
sr = the radial spacing of perimeters of shear reinforcement
fywd,ef = 250 + 0.25 d ≤ fywd
α = the angle between the shear reinforcement and the slab plane
According to DIN EN 1992-1-1 / NA [2], the amount of reinforcement in the first shear reinforcement perimeter must be increased by the factor κsw,1 = 2.5, and by κsw,2 = 1.4 in the second shear reinforcement perimeter.
The punching shear reinforcement should be placed up to a distance of 1.5d from the outermost perimeter. The required length of the outermost perimeter is uout,ef, which is defined according to Eq. 6.54 of EC 2 [1]:
Conclusion
The provisions for punching shear design according to Eurocode 2 cannot be applied efficiently without a software solution. An example is the calculation of the load increment factor β based on the model with fully plastic shear force distribution in the control perimeter, or the iterative calculation of the basic control perimeter area of foundations. Also, ground plans of buildings are designed in a freer and more complex way, so it is impossible to follow the simplification rules; thus, they also cannot be applied. The RF-PUNCH Pro add-on module of the structural FEA software RFEM allows you to take all the data required for the geometrical determination of the basic control perimeter and design loads for the punching shear design directly from the FEM entries or FEM calculation. Thus, the punching shear design of columns, wall corners, and wall ends can be performed very easily and efficiently. For columns, there is the additional option to consider an enlarged column head. The results of the punching shear design are displayed in clearly arranged result tables, including all intermediate results relevant for the individual design checks. The results as well as the required punching shear reinforcement, shear force distribution, and punching shear resistances can be displayed graphically in the RFEM graphic window.