Calcul direct des déformations

par la méthode de la rigidité effective (MRE)

1. Description des principes théoriques

Pour l’analyse de déformation dans le cadre de la vérification du béton, une méthode analytique est utilisée pour les structures 2D et les éléments 1D soumis à des efforts normaux et à des moments fléchissants. Celle-ci repose sur le calcul de rigidités effectives (méthode de la rigidité effective) au niveau de la section, en tenant compte de l’état de fissuration, ainsi que des effets comme le raidissement en traction et des effets de long terme simples (retrait et fluage).

1.1. Hypothèses fondamentales sur les matériaux et la géométrie

Pour l’analyse directe des déformations dans la vérification du béton, un comportement linéaire-élastique en compression et un comportement linéaire-élastique jusqu’à atteindre la résistance en traction sont présumées. Ces hypothèses suffisent pour la vérification à l’ELS. Si les contraintes dépassent la résistance du béton en compression, le développement de l’endommagement intervient conformément à l’EN 1992-1-1, 7.3.4.
Le calcul repose sur un modèle isotrope simple de la mécanique de la rupture, défini individuellement pour les deux directions d’armature. Conformément à l’EN 1992-1-1, une matrice de rigidité effective des matériaux est calculée par interpolation entre l’état non fissuré (état I) et l’état fissuré (état II) selon la clause 7.4.3, équation (7.18). Le béton armé est ainsi modélisé comme un matériau orthotrope. Des effets tels que le raidissement en traction et des effets de long terme simples (retrait et fluage) sont pris en compte.
Le calcul des matrices de rigidité des matériaux est réalisé pour les types de modèle 2D-XY (u_z / φ_x / φ_y) et 3D. Pour le modèle 3D, l’influence des excentrements des centres de gravité idéaux dans la matrice de rigidité est également prise en compte.

1.2. Efforts internes de calcul

Comme décrit ci-dessus, le calcul des rigidités repose sur des hypothèses linéaires-élastiques. Les efforts internes sont transformées orthogonalement à la direction des armatures ф et sur les deux surfaces s (en haut et en bas). Les efforts internes résultants – moments fléchissants m_s,ф et efforts normaux n_s,ф (les moments de torsion sont éliminés par transformation) – dépendent de :
(a) Type de modèle ;
(b) Méthode de calcul ;
(c) Critère de classification.

1.3. Surface critique

Pour la détermination de la surface critique, chaque direction d’armature ф est considérée séparément. L’état de contrainte est analysé sur la surface inférieure (en direction de l’axe local +z) et sur la surface supérieure (en direction de l’axe local -z). La surface ayant la contrainte en traction du béton la plus importante est considérée comme déterminante. Les efforts internes sur les surfaces critiques sont désignées par n_ф et m_ф.

L’effort normal n_ф,s, transformé en direction d’armature ф, a la même valeur pour les deux surfaces (n_ф = n_ф,haut = n_ф,bas). Par conséquent, les efforts normaux ne sont pas pertinents pour la détermination de la surface critique, seuls les moments fléchissants sont considérés pour déterminer la surface déterminante. Les signes des moments fléchissants m_ф,s sont déterminés en fonction de si les moments induisent une traction ou une compression sur la surface respective. La surface critique est celle avec le moment fléchissant le plus important (c’est-à-dire la surface la plus sollicitée en traction).

Pour le calcul des rigidités, seuls les efforts internes n_ф et m_ф sur la surface critique sont pris en compte. Jusqu’à présent, le terme « surface inférieure » faisait référence à l’axe local +z. Ci-après, « surface inférieure » fait référence à la face déterminante de la surface.

1.4. Propriétés de la section

Les propriétés de la section sont déterminées pour les deux directions d’armature et pour les deux états de la section c (fissuré / non fissuré). Pour l’état I (section non fissurée), un comportement linéaire-élastique du béton en traction est présumé. Pour l’état II (section fissurée), la résistance en traction du béton n’est pas prise en compte.

Le calcul des paramètres géométriques est, pour l'état I, indépendant des efforts internes, ce qui permet un calcul direct. Pour l’état II, la profondeur de l’axe neutre est calculée de manière itérative. Pour des raisons numériques, le logiciel utilise le ratio d’armatures minimal ρ_min = 10^-4 pour les deux surfaces déterminantes (en haut et en bas), mais uniquement en cas de composante d’effort normal positive. Cela signifie qu’en l’absence d’armature, une aire minimale virtuelle d’armature est supposée. Une valeur aussi faible n’a pas d’impact notable sur les résultats (rigidités).

Les propriétés idéales de la section calculées (par rapport à la section en béton) en direction d'armature ф et pour l’état de fissuration c sont :
(a) Moment d’inertie par rapport au centre de gravité idéal I_c,ф
(b) Moment d’inertie par rapport au centre de gravité géométrique de la section I_0,c,ф
(c) Aire de la section A_c,ф
(d) Excentrement du centre de gravité idéal e_c,ф

1.5. Effets à long terme

Le retrait et le fluage sont des propriétés du béton dépendantes du temps. Conformément à l’EN 1992-1-1, les effets à long terme doivent être pris en compte séparément.

1.5.1. Fluage

Les effets du fluage sont pris en compte par une réduction du module d’élasticité du béton E_c, en utilisant le coefficient de fluage effectif ϕ_eff selon l’EN 1992-1-1, équation (7.20) :

1.5.2. Retrait

Dans la vérification de la flèche selon l’EN 1992-1-1, deux aspects sont influencés par les effets de retrait.

1.5.2.1. Réduction de la rigidité du matériau
La rigidité du matériau dans chaque direction d’armature φ est réduite par un coefficient d’influence du retrait dit k_sh,c,φ. Pour les deux états de fissuration c (fissuré / non fissuré), les efforts normaux de retrait n_sh,c,φ et les moments fléchissants m_sh,c,φ sont déterminés à partir de la déformation libre due au retrait ε_sh :

Fig. 1.1: Efforts internes n_sh,ф et m_sh,ф
Avec ces efforts internes résultant du retrait, la courbure supplémentaire κ_sh,c,ф au point analysé est calculée, sans l’influence du modèle environnant. Ensuite, le coefficient d’influence du retrait

Le coefficient k_sh,c,ф est limité à la plage k_sh,c,ф∈ (1, 100). Ainsi, k_sh,c,ф ne peut pas réduire la rigidité plus de 100 fois (pour des raisons numériques et physiques). La valeur minimale k_sh,c,ф = 1,0 signifie que l’influence du retrait ne peut pas être prise en compte si celle-ci a une orientation opposée à la courbure causée par la charge κ_d. Si le retrait est désactivé, le coefficient k_sh,c,ф = 1,0.
L’influence du retrait sur la rigidité de la membrane n’est pas prise en compte.

1.5.2.2. Calcul du coefficient de distribution
La deuxième influence du retrait concerne le calcul du coefficient de distribution (paramètre de dommage) ζ selon l’EN 1992-1-1, 7.4.3, équation (7.18). Le coefficient de distribution est détaillé dans le chapitre suivant.

1.6. Coefficient de distribution

Le calcul du coefficient de distribution ζ_d est présenté pour la direction d’armature ф. Tout d’abord, le logiciel calcule la contrainte en traction maximale du béton σ_max,ф en supposant un comportement linéaire-élastique du matériau. Si les effets à long terme (fluage ou retrait) sont activés, la contrainte maximale doit être calculée deux fois, sinon une seule fois.

Calcul à court terme : Vérifie si des fissures apparaissent immédiatement après la charge.
Calcul à long terme : Prend en compte le comportement en cas de fissures avec influence du fluage ou du retrait à la fin de la période considérée.

Étapes de calcul :
Si le fluage est activé : Les paramètres géométriques à court terme et la contrainte maximale sont calculés.
Si le retrait activé : Il est seulement nécessaire de recalculer la contrainte à court terme. Ensuite, la contrainte maximale finale σ_max,ф est calculée comme le maximum de la contrainte à long terme σ_max,lt,ф et la contrainte à court terme σ_max,st,ф.

L’influence de la force de retrait sur la contrainte maximale en traction σ_max,ф est prise en compte par les efforts internes supplémentaires résultant du retrait. Le calcul du coefficient de distribution ζ_d,ф dépend du fait que le raidissement en traction soit pris en compte lors du calcul de la déformation, selon l’EN 1992-1-1.

1.6.1. Coefficient de distribution ζ_d,ф en tenant compte du raidissement en traction

1.6.2. Coefficient de distribution ζ_d,ф sans tenir compte du raidissement en traction

1.6.3. Détection de l’état de fissuration

La détection de l’état de fissuration peut être configurée dans la configuration pour l’ELS. Les options suivantes sont disponibles :
(a) L’état de fissuration est calculé en fonction de la charge associée ;
(b) L’état de fissuration basé sur la combinaison caractéristique associée (CO) de la situation de projet à l’ELS ;
(c) L’état de fissuration déterminé comme l’enveloppe de toutes les situations de projet à l’ELS ;
(d) L’état de fissuration indépendant de la charge.

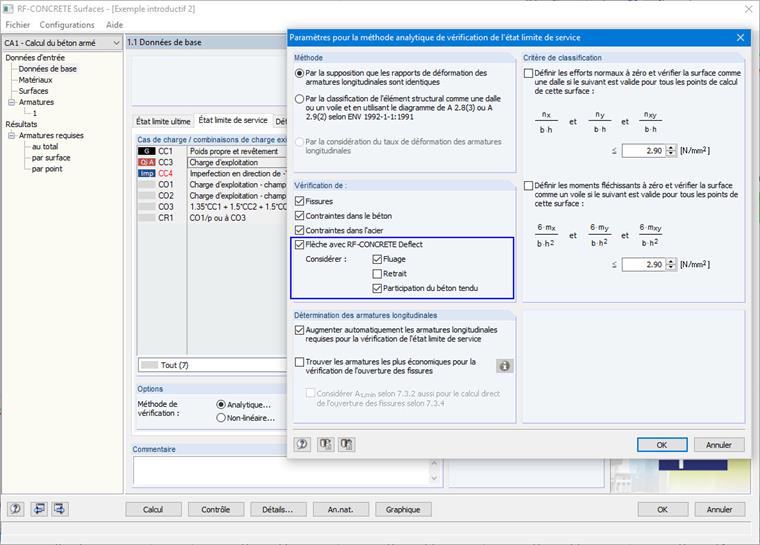
Fig. 1.2: Configuration pour l’ELS
Si l’option État de fissuration calculé en fonction de la charge associée est sélectionnée, l’état de fissuration (coefficient de distribution ζ_d) est calculé uniquement en fonction de la charge actuelle (combinaison de charge).
Si l’option État de fissuration basé sur la combinaison caractéristique associée (CO) de la situation de projet à l’ELS est sélectionnée, le coefficient de distribution ζ_d est calculé comme le maximum parmi toutes les charges associées. Les charges associées peuvent être définies dans la définition de la combinaison de charges.

Fig. 1.3: Charges associées
Si l’option État fissuré déterminé sous forme d'enveloppe à partir de toutes les situations de projet à l’ELS est sélectionnée, le coefficient de distribution ζ_d est calculé comme le maximum de toutes les situations de projet. Si l’option État de fissuration indépendant de la charge est sélectionnée, le coefficient de distribution vaut toujours 1,0.

1.6.4. Situations de projet

En général, la déformation est calculée pour les charges quasi-permanentes. Cependant, il est possible de sélectionner les situations de projet souhaitées (dans la configuration pour l’ELS, l’option d’attribution personnalisée du type de situation de projet), pour lesquelles la déformation doit être calculée.
Les types de situations de projet pour l’ELS suivants sont disponibles :
- Quasi-permanente,
- Fréquente,
- Caractéristique.
Pour chaque type, une limite de déformation peut être définie (voir la Fig. 1.2). De plus, les situations de projet souhaitées sont également paramétrées pour la vérification du béton.

Fig. 1.4: Paramètre des situations de projet pour la vérification du béton
Pour la détection de l’état de fissuration (notamment lors du choix de savoir si la détection provient des charges associées ou de toutes les situations de projet pour l’ELS), le paramétrage de la vérification du béton est crucial.
Autrement dit :
- Si une situation de projet est désactivée dans la configuration pour l’ELS mais activée dans les paramètres pour la vérification du béton, elle sera prise en compte.
- Si une situation de projet est activée dans la configuration pour l’ELS mais désactivée dans les paramètres pour la vérification du béton, elle ne sera pas prise en compte.

1.7. Propriétés de la section pour l’analyse des déformations

Dans la matrice de rigidité des matériaux D pour l’analyse des déformations, le logiciel a besoin des propriétés de la section dans chaque direction d’armature, en fonction de l’état de fissuration. Ces propriétés sont :
(a) Moment d’inertie par rapport au centre de gravité idéal I_ф ;
(b) Moment d’inertie par rapport au centre de gravité géométrique de la section I_0,c ;
(c) Aire de section idéale A_ф ;
(d) Excentrement du centre de gravité idéal e_ф par rapport au centre de gravité géométrique.
Une déformation moyenne ε_ф et une courbure moyenne κ_ф sont calculées par interpolation entre l’état fissuré et non fissuré selon l’EN 1992-1-1, équation (7.18) :

La déformation à l’état non fissuré et fissuré c (état I et II) est calculée selon les équations suivantes :

Les propriétés idéales de la section sont calculées par rapport au centre de gravité idéal de la section. L’influence du retrait est prise en compte par le facteur k_sh,c,ф :

Si l’effort normal est différent de zéro, les propriétés de la section sont calculées par rapport au centre de gravité géométrique de la section, en tenant compte de l’excentrement :

1.8. Matrice de rigidité des matériaux D (barres)

La rigidité axiale EA et la rigidité en flexion EI_y,0 ne sont calculées qu’en direction de l’armature ф = 1 (direction de la barre) comme suit :

1.9. Matrice de rigidité des matériaux D (surfaces)

Lors du calcul des propriétés de la section, la valeur initiale du coefficient de Poisson ν_init est réduite indépendamment dans les deux directions selon l’équation suivante :

La matrice de rigidité des matériaux est calculée selon la théorie des surfaces orthotropes.

1.9.1. Rigidité en flexion - Plaques et coques

Les rigidités en flexion dans les directions d'armature ф sont déterminées comme suit :
Pour les coques :

Pour les plaques :
La composante non diagonale de la matrice de rigidité des matériaux est identique pour les plaques et les coques :
Pour les coques, les différences dans les rigidités en flexion en raison des moments d’inertie sont compensées par les composantes d’excentrement dans la matrice de rigidité des matériaux.

1.9.2. Rigidité en torsion des plaques et coques

Les éléments de la matrice de rigidité pour les plaques et coques sont calculés comme suit :

1.9.3. Rigidité en cisaillement des plaques et coques

Les éléments de la matrice de rigidité pour le cisaillement ne sont pas réduits lors de l’analyse de déformation. Ils sont calculés à partir du module de cisaillement G de la section idéale et de la hauteur de la section h. L’expression est identique pour les coques et les plaques :

1.9.4. Rigidité de membrane des coques

Les rigidités de membranes dans les directions d’armature ф sont calculées comme suit :

La partie non diagonale de la matrice de rigidité du matériau est déterminée par :

La partie composante de la rigidité en cisaillement est :

1.9.5. Excentrement - Coques

Les éléments de la matrice de rigidité pour l’excentrement du centre de gravité (section idéale) en direction d’armature ф sont calculés comme suit :

La partie non diagonale de la matrice de rigidité des matériaux est déterminée par :

La composante d’excentrement pour la torsion est calculée comme suit :

1.9.6. Test de définition positive

La définition positive de la matrice de rigidité des matériaux D est testée en utilisant un critère de SYLVESTER modifié (en tenant compte des blocs nuls).
Si la matrice de rigidité D n’est pas définie positive, les composants non diagonaux de la matrice de rigidité des matériaux sont successivement mis à zéro. Dans le pire des cas, seuls les composants positifs de la diagonale principale restent.

1.10. Calcul des déformations

Les déformations d’un objet (barre ou surface) sont déterminées à l’aide de la matrice de rigidité D préalablement calculée. La valeur de calcul (ratio de vérification) est calculée à partir de la déformation et de la limite prescrite.

1.10.1. Charge associée

Lorsqu’une charge associée est assignée à la charge principale, la déformation finale est calculée comme la somme des valeurs individuelles. La combinaison de charge principale est calculée sans propriétés dépendantes du temps (fluage et retrait) et doit donc être à court terme (fréquente ou caractéristique). La combinaison de charges associée est, quant à elle, toujours calculée avec des propriétés dépendantes du temps et devrait donc être à long terme (quasi-permanente). Si plus d’une charge associée est assignée, celle avec la valeur la plus élevée de déformation est considérée.
La déformation totale est calculée comme suit :

1.11 Différences entre RFEM 5 et RFEM 6

Calcul de la hauteur de la zone de compression du béton
Dans RFEM 5, la hauteur de la zone de compression du béton est calculée sur la base de la hauteur nette de la section, tandis que dans RFEM 6, la hauteur brute de la section est utilisée. Cette procédure permet un calcul plus rapide et plus clair, ce qui facilite également la traçabilité des résultats. Grâce à cette simplification, la précision du calcul demeure élevée, de sorte que les résultats n’indiquent pas de différences significatives dans la pratique. RFEM 6 offre ainsi une solution plus efficace pour des résultats qui restent précis.

Facteur de distribution des armatures
Le facteur de répartition qui décrit la distribution des contraintes sur la section était déterminé dans RFEM 5 exclusivement sur la base de la contrainte à long terme. Cela signifie que seule la contrainte agissant sur une période prolongée était prise en compte. Dans RFEM 6, l'approche de calcul a été développée pour permettre de prendre en compte le maximum de la contrainte à long terme et à court terme. Ce changement permet une représentation plus réaliste des conditions de contrainte réelles dans la section.