Calcolo diretto della deformazione

mediante Metodo della Rigidezza Effettiva (ESM)

1. Descrizione dei fondamenti teorici

Per l'analisi delle deformazioni nell'ambito della progettazione del calcestruzzo, viene utilizzato un procedimento analitico per strutture 2D ed elementi 1D sottoposti a forze normali e momenti flettenti. Questo si basa sulla determinazione delle rigidezze effettive (Metodo della Rigidezza Effettiva) a livello di sezione trasversale considerando lo stato di fessurazione, includendo effetti come Tension Stiffening e l'effetto a lungo termine (ristagno e scorrimento).

1.1. Ipotesi di base sui materiali e la geometria

Per l'analisi diretta delle deformazioni nella progettazione del calcestruzzo, si assume un comportamento a compressione lineare-elastico e un comportamento lineare-elastico fino al raggiungimento della resistenza a trazione. Tali ipotesi sono sufficienti per la verifica di servizio. Se le tensioni superano la resistenza a compressione del calcestruzzo, si verifica lo sviluppo del danno secondo EN 1992-1-1, Sezione 7.3.4. Il calcolo si basa su un modello isotropo semplificato della meccanica della frattura, definito singolarmente per le due direzioni di armatura. Secondo EN 1992-1-1, una matrice di rigidezza del materiale effettiva viene calcolata per interpolazione tra stato non fessurato (Stato I) e stato fessurato (Stato II) secondo Sezione 7.4.3, Equazione (7.18). Il calcestruzzo armato è modellato quindi come materiale ortotropo. Vengono considerati effetti come il Tension Stiffening e semplici effetti a lungo termine (ristagno e scorrimento). Il calcolo delle matrici di rigidezza del materiale è implementato per i tipi di modello 2D-XY (u_z / φ_x / φ_y) e 3D. Nel modello 3D viene considerato anche l'influenza delle eccentricità dei punti centrali ideali nella matrice di rigidezza.

1.2. Forze interne nel progetto

Come descritto sopra, il calcolo delle rigidezze si basa su ipotesi lineari - elastiche. Le forze interne vengono trasformate ortogonalmente alla direzione dell'armatura φ e sulle due superfici s (superiore e inferiore). Le forze interne ottenute - momenti flettenti m_s,φ e forze normali n_s,φ (momenti torcenti vengono eliminati tramite trasformazione) dipendono da: (a) Tipo di modello; (b) Metodo di calcolo; (c) Criterio di classificazione.

1.3. Superficie critica

Per determinare la superficie critica, ogni direzione di armatura φ è considerata separatamente. Lo stato di tensione viene analizzato sulla superficie inferiore (nella direzione dell'asse +z locale) e sulla superficie superiore (nella direzione dell'asse -z locale). La superficie con la maggiore tensione di trazione del calcestruzzo è considerata determinante. Le forze interne sulle superfici critiche sono indicate come n_φ e m_φ.

La forza normale n_φ,s, trasformata nella direzione di armatura φ, ha lo stesso valore per entrambe le superfici (n_φ = n_φ,sup = n_φ,inf). Pertanto, le forze normali non sono rilevanti per determinare la superficie critica; solo i momenti flettenti vengono considerati per trovare la superficie determinante. L'orientamento dei momenti flettenti m_φ,s viene determinato in base al fatto che i momenti causino trazione o compressione sulla superficie corrispondente. La superficie critica è quella con il maggiore momento flettente (cioè la superficie più sollecitata a trazione).

Per il calcolo delle rigidezze, vengono considerate solo le forze interne n_φ e m_φ sulla superficie critica. Fino ad ora, il termine "superficie inferiore" si riferiva all'asse +z locale. D'ora in poi, "superficie inferiore" si riferisce al lato determinante della superficie.

1.4. Proprietà della sezione trasversale

Le proprietà della sezione trasversale vengono determinate per entrambe le direzioni di armatura e per entrambi gli stati della sezione c (fessurato/non fessurato). Per lo stato I (sezione non fessurata) si assume un comportamento lineare - elastico del calcestruzzo sotto trazione. Per lo stato II (sezione fessurata) non si considera la resistenza a trazione del calcestruzzo.

Il calcolo dei parametri geometrici è indipendente dalle forze interne per lo stato I, consentendo un calcolo diretto. Per lo stato II, la profondità dell'asse neutro viene calcolata iterativamente. Per motivi numerici, il programma utilizza il minimo grado di armatura ρ_min = 10^-4 per entrambe le superfici determinanti (superiore e inferiore), ma solo in presenza di componente di forza normale positiva. Questo significa che, in caso di mancanza di armatura, viene ipotizzata una superficie di armatura virtuale minima. Un valore così piccolo non ha un'influenza significativa sui risultati (rigidezze).

Le proprietà ideali della sezione trasversale (riferite alla sezione in calcestruzzo) in una direzione di armatura φ e per lo stato di fessurazione c sono: (a) Momento d'inerzia rispetto al baricentro ideale I_c,φ (b) Momento d'inerzia rispetto al baricentro geometrico della sezione I_0,c,φ (c) Area della sezione trasversale A_c,φ (d) Eccentricità del baricentro ideale e_c,φ

1.5. Effetti a lungo termine

Il ristagno e lo scorrimento sono proprietà a tempo dipendente del calcestruzzo. Secondo EN 1992-1-1 vi sono separatamente considerati gli effetti a lungo termine.

1.5.1. Scorrimento

Gli effetti del scorrimento sono considerati riducendo il modulo di elasticità del calcestruzzo E_c utilizzando il coefficiente di scorrimento efficace ϕ_eff secondo EN 1992-1-1, Equazione (7.20):

1.5.2. Ristagno

Nel calcolo della deformazione secondo EN 1992-1-1, vi sono due aspetti influenzati dal ristagno.

1.5.2.1. Riduzione della rigidezza del materiale La rigidezza del materiale in ogni direzione di armatura φ viene ridotta da un cosiddetto coefficiente di influenza del ristagno k_sh,c,φ. Per entrambi gli stati di fessurazione c (fessurato/non fessurato), si determinano le forze normali di ristagno n_sh,c,φ e i momenti flettenti m_sh,c,φ dalla deformazione libera di ristagno ε_sh:

Fig. 1.1: Forze interne n_sh,f e m_sh,f Con queste forze interne derivanti dal ristagno, si calcola la curvatura aggiuntiva κ_sh,c,φ nel punto analizzato, senza l'influenza del modello circostante. Successivamente, viene calcolato il coefficiente di influenza del ristagno

Il coefficiente k_sh,c,φ è limitato all'intervallo k_sh,c,φ ∈ (1, 100). Pertanto, k_sh,c,φ non può ridurre la rigidità di oltre 100 volte (per ragioni numeriche e fisiche). Il valore minimo k_sh,c,φ = 1,0 indica che l'influenza del ristagno non può essere considerata se questa ha un'orientazione opposta alla curvatura κ_d causata dal carico. Se il ristagno è disattivato, il coefficiente k_sh,c,φ = 1,0. L'influenza del ristagno sulla rigidezza della membrana non è considerata.

1.5.2.2. Calcolo del coefficiente di distribuzione Il secondo effetto del ristagno riguarda il calcolo del coefficiente di distribuzione (parametro di danno) ζ secondo EN 1992-1-1, Sezione 7.4.3, Equazione (7.18). Il capitolo seguente descrive il coefficiente di distribuzione nel dettaglio.

1.6. Coefficiente di distribuzione

Il calcolo del coefficiente di distribuzione ζ_d è presentato per la direzione di armatura φ. Per prima cosa, il programma calcola la massima tensione di trazione del calcestruzzo σ_max,φ assumendo un comportamento del materiale lineare-elastico. Se sono attivati gli effetti a lungo termine (scorrimento o ristagno), è necessario calcolare la massima tensione due volte, altrimenti solo una volta.

Calcolo a breve termine: Controlla se le fessure si sviluppano immediatamente dopo il carico. Calcolo a lungo termine: Considera il comportamento della fessura con l'influenza dello scorrimento o del ristagno alla fine del periodo di tempo considerato.

Passi di calcolo: Con scorrimento attivato: Vengono calcolati i parametri geometrici a breve termine e la massima tensione. Con ristagno attivato: È necessario soltanto ricalcolare la tensione a breve termine. Successivamente, la tensione massima finale σ_max,φ viene calcolata come massimo tra la tensione a lungo termine σ_max,lt,φ e la tensione a breve termine σ_max,st,φ:

L'influenza della forza di ristagno sulla massima tensione di trazione σ_max,φ viene considerata tramite le forze interne aggiuntive derivate dal ristagno. Il calcolo del coefficiente di distribuzione ζ_d,φ dipende se il Tension-Stiffening è considerato nella analisi della deformazione secondo EN 1992-1-1.

1.6.1. Coefficiente di distribuzione ζ_d,φ con considerazione del Tension-Stiffening

1.6.2. Coefficiente di distribuzione ζ_d,φ senza considerazione del Tension-Stiffening

1.6.3. Riconoscimento dello stato di fessurazione

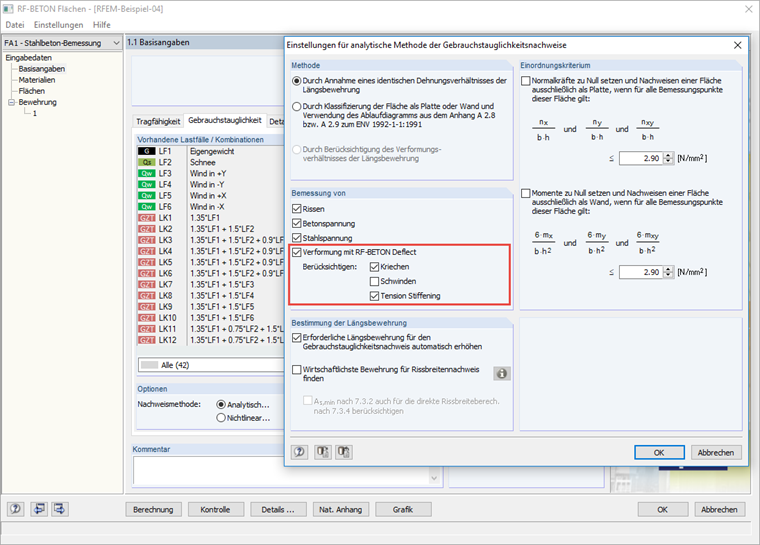
Il riconoscimento dello stato di fessurazione può essere impostato nella configurazione di servizio. Sono disponibili le seguenti opzioni: (a) Lo stato di fessurazione è calcolato in base al carico associato; (b) Stato di fessurazione basato sulla combinazione caratteristica associata (CO) della situazione di progettazione SLS; (c) Stato di fessurazione determinato come inviluppo di tutte le situazioni di progettazione SLS; (d) Stato di fessurazione indipendente dal carico.

Fig. 1.2: Configurazione di servizio Se viene selezionata l'opzione Lo stato di fessurazione è calcolato in base al carico associato, lo stato di fessurazione (coefficiente di distribuzione ζ_d) viene calcolato solo in base al carico attuale (combinazione di carico). Se viene selezionata l'opzione Stato di fessurazione basato sulla combinazione caratteristica associata (CO) della situazione di progettazione SLS, il coefficiente di distribuzione ζ_d viene calcolato come massimo di tutti i carichi associati. I carichi associati possono essere stabiliti nella definizione della combinazione di carico.

Fig. 1.3: Carichi correlati Se viene selezionata l'opzione Stato di fessurazione determinato come inviluppo di tutte le situazioni di progettazione SLS, il coefficiente di distribuzione ζ_d viene calcolato come massimo di tutte le situazioni di progettazione. Se viene selezionata l'opzione Stato di fessurazione indipendente dal carico, il coefficiente di distribuzione è sempre pari a 1,0.

1.6.4. Situazioni di progettazione

In generale, la deviazione viene calcolata per carichi quasi-permanenti. È tuttavia possibile selezionare le situazioni di progettazione desiderate (nella configurazione di servizio, opzione Assegnazione personalizzata del tipo di situazione di progettazione) per le quali calcolare la deviazione. Possono essere selezionati i seguenti tipi di situazione di progettazione di servizio: - Quasi - permanente, - Frequente, - Caratteristico. Per ogni tipo, è possibile stabilire un limite per la deviazione (vedere Fig. 1.2). Inoltre, si determina anche per la progettazione del calcestruzzo le situazioni di progettazione desiderate.

Fig. 1.4: Impostazione delle situazioni di progettazione per la progettazione del calcestruzzo Per il riconoscimento dello stato di fessurazione (in particolare nella selezione se il riconoscimento avviene da carichi associati o da tutte le situazioni di progettazione di servizio) è decisiva l'impostazione nella progettazione del calcestruzzo. In altre parole: - Se una situazione di progettazione è disattivata nella configurazione di servizio ma attivata nell'impostazione della progettazione del calcestruzzo, essa è considerata. - Se una situazione di progettazione è attivata nella configurazione di servizio ma disattivata nell'impostazione della progettazione del calcestruzzo, essa non è considerata.

1.7. Proprietà della sezione trasversale per l'analisi delle deformazioni

Nella matrice di rigidezza del materiale D per l'analisi delle deformazioni, il programma necessita delle proprietà della sezione trasversale in ogni direzione di armatura, a seconda dello stato di fessurazione. Queste sono: (a) Momento d'inerzia rispetto al baricentro ideale I_φ; (b) Momento d'inerzia rispetto al baricentro geometrico della sezione I_0,c; (c) Area della sezione trasversale ideale A_φ; (d) Eccentricità del baricentro ideale e_φ rispetto al baricentro geometrico. Una deformazione media ε_φ e una curvatura media κ_φ vengono calcolate per interpolazione tra stato fessurato e non fessurato secondo EN 1992-1-1, Equazione (7.18):

La deformazione in stato non fessurato e fessurato c (Stato I e II) viene calcolata secondo le equazioni seguenti: Le proprietà ideali della sezione trasversale vengono calcolate rispetto al baricentro ideale della sezione. L'influenza del ristagno viene considerata tramite il fattore k_sh,c,φ : Se la forza normale è diversa da zero, le proprietà della sezione trasversale vengono calcolate rispetto al baricentro geometrico della sezione considerando l'eccentricità:

1.8. Matr Transenna di Rigidezza Materiale D (Aste)

La rigidezza assiale EA e la rigidezza flessionale EI_y,0 vengono calcolate solo nella direzione di armatura φ = 1 (direzione dell'asta) come segue:

1.9. Matr Transenna di Rigidezza Materiale D (Superfici)

Nel calcolo delle proprietà della sezione trasversale, il valore iniziale del rapporto di Poisson ν_init in entrambe le direzioni viene ridotto indipendentemente secondo la seguente equazione:

La matrice di rigidezza del materiale viene calcolata secondo la teoria per superfici ortotropiche.

1.9.1. Rigidezza alla flessione - Piastre e Scocche

Le rigidezze di flessione nelle direzioni di armatura φ vengono determinate come segue: Per scocche:

Per piastre: La componente non diagonale della matrice di rigidezza del materiale è identica per piastre e scocche: Per le scocche, le differenze nelle rigidezze alla flessione dovute ai momenti d'inerzia vengono compensate dalle componenti d'eccentricità nella matrice di rigidezza del materiale.

1.9.2. Rigidezza torcente di piastre e scocche

Gli elementi della matrice di rigidezza vengono calcolati per piastre e scocche come segue:

1.9.3. Rigidezza al taglio di piastre e scocche

Gli elementi della matrice di rigidezza per il taglio non vengono ridotti nell'analisi delle deformazioni. Vengono calcolati dal modulo di taglio G della sezione ideale e dall'altezza della sezione h. L'espressione è identica per scocche e piastre:

1.9.4. Rigidezza di membrana di scocche

Le rigidezze di membrana nelle direzioni di armatura φ vengono calcolate come segue:

La parte non diagonale della matrice di rigidezza del materiale è determinata da: La componente di rigidezza al taglio è data da:

1.9.5. Eccentricità – Scocche

Gli elementi della matrice di rigidezza per l'eccentricità del baricentro (sezione ideale) nella direzione di armatura φ vengono calcolati come segue:

La parte non diagonale della matrice di rigidezza del materiale è determinata da: La componente d'eccentricità per la torsione viene calcolata come segue:

1.9.6. Test di definizione positiva

La definizione positiva della matrice di rigidezza del materiale D viene testata tramite un criterio di Sylvester modificato (considerando i blocchi nulli). Se la matrice di rigidezza D non è definita positivamente, le componenti non diagonali della matrice di rigidezza del materiale vengono rese nulle progressivamente. Nell'estremo caso, restano solamente le componenti positive della diagonale principale.

1.10. Calcolo delle deformazioni

Le deformazioni di un oggetto (asta o superficie) vengono determinate utilizzando la matrice di rigidezza D calcolata in precedenza. Il valore di progetto (rapporto di design) viene calcolato dalla deformazione e dal limite.

1.10.1. Carico correlato

Se viene assegnato un carico correlato al carico principale, la deformazione finale è calcolata come somma dei singoli valori. La combinazione di carico principale viene calcolata senza proprietà dipendenti dal tempo (scorrimento e ristagno) e deve quindi essere a breve termine (frequente o caratteristica). La combinazione di carico correlata viene invece sempre calcolata con proprietà dipendenti dal tempo e dovrebbe quindi essere a lungo termine (quasi - permanente). Se viene assegnato più di un carico correlato, viene considerato il valore di deformazione più alto. La deformazione totale viene calcolata come segue:

1.11 Differenze tra RFEM 5 e RFEM 6

Calcolo dell'altezza della zona di compressione del calcestruzzo In RFEM 5, l'altezza della zona di compressione del calcestruzzo è calcolata basandosi sull'altezza netta della sezione, mentre in RFEM 6 viene utilizzata l'altezza lorda della sezione. Questo approccio consente un calcolo più rapido e chiaro, che consente anche una migliore comprensibilità dei risultati. Con questa semplificazione, la precisione del calcolo rimane elevata, quindi i risultati in pratica non presentano differenze significative. RFEM 6 offre quindi una soluzione più efficiente mantenendo risultati precisi.

Coefficiente di distribuzione dell'armatura Il coefficiente di distribuzione, che descrive la distribuzione delle tensioni attraverso la sezione, è stato determinato in RFEM 5 esclusivamente sulla base della tensione a lungo termine. Ciò significava che veniva considerata solo la tensione che agisce per un periodo prolungato. In RFEM 6, l'approccio di calcolo è stato sviluppato ulteriormente in modo che ora venga considerato il massimo sia della tensione a lungo termine che della tensione a breve termine. Questa modifica garantisce una rappresentazione più realistica delle condizioni di tensione effettive nella sezione.