Cálculo de deformação direta

usando o Método de Rigidez Eficaz (ESM)

1. Descrição do contexto teórico

Para a análise de deformação no dimensionamento de concreto, é utilizado um método analítico para estruturas 2D e elementos 1D, sujeitos a forças normais e momentos de flexão. Este método baseia-se na determinação de rigidezes eficazes (Método de Rigidez Eficaz) no nível da seção transversal, considerando o estado de fissuração, bem como efeitos como Tension Stiffening e efeitos simples de longo prazo (retração e fluência).

1.1. Suposições básicas de material e geometria

Para a análise direta de deformações no dimensionamento de concreto, são assumidos comportamento linear-elástico em compressão e comportamento linear-elástico até alcançar a resistência à tração. Tais suposições são suficientes para a verificação da aptidão ao uso. Se as tensões excederem a resistência à compressão do concreto, o desenvolvimento de danos segue a EN 1992-1-1, seção 7.3.4. O cálculo baseia-se num modelo isotrópico simples de mecânica de fratura, definido individualmente para as duas direções de armadura. De acordo com a EN 1992-1-1, é calculada uma matriz de rigidez de material eficaz por interpolação entre o estado não fissurado (Estado I) e o estado fissurado (Estado II) conforme a seção 7.4.3, equação (7.18). Assim, o concreto armado é modelado como um material ortotrópico. Efeitos como Tension Stiffening e efeitos simples de longo prazo (retração e fluência) são considerados. O cálculo das matrizes de rigidez do material é implementado para os tipos de modelo 2D-XY (u_z / φ_x / φ_y) e 3D. No modelo 3D, o efeito das excentricidades dos centros de gravidade ideais é adicionalmente considerado na matriz de rigidez.

1.2. Forças internas de dimensionamento

Como descrito acima, o cálculo das rigidezes baseia-se em suposições linear-elásticas. As forças internas são transformadas ortogonalmente à direção da armadura ф e nas duas superfícies s (superior e inferior). As forças internas obtidas – momentos de flexão m_s,ф e forças normais n_s,ф (os momentos de torção são eliminados pela transformação) – dependem de: (a) Tipo de modelo; (b) Método de cálculo; (c) Critério de classificação.

1.3. Superfície crítica

Para determinar a superfície crítica, cada direção de armadura ф é considerada separadamente. O estado de tensão é analisado na superfície inferior (na direção do eixo local +z) e na superfície superior (na direção do eixo local -z). A superfície com a maior tensão de tração no concreto é considerada a determinante. As forças internas nas superfícies críticas são designadas como n_ф e m_ф.

A força normal n_ф,s, transformada na direção da armadura ф, tem o mesmo valor para ambas as superfícies (n_ф = n_ф,superior = n_ф,inferior). Portanto, as forças normais não são relevantes para determinar a superfície crítica; somente os momentos de flexão são considerados para encontrar a superfície determinante. Os sinais dos momentos de flexão m_ф,s são determinados de acordo com se os momentos causam tração ou compressão na respectiva superfície. A superfície crítica é aquela com o maior momento de flexão (isto é, a superfície mais solicitada à tração).

Para o cálculo das rigidezes, apenas as forças internas n_ф e m_ф na superfície crítica são consideradas. Até agora, o termo "superfície inferior" referia-se ao eixo local +z. No entanto, a seguir, "superfície inferior" refere-se ao lado determinante da superfície.

1.4. Propriedades da seção transversal

As propriedades da seção transversal são determinadas para ambas as direções de armadura e para ambos os estados de seção c (fissurado / não fissurado). Para o Estado I (seção não fissurada), é assumido um comportamento linear-elástico do concreto em tração. Para o Estado II (seção fissurada), a resistência à tração do concreto não é considerada.

O cálculo dos parâmetros geométricos para o Estado I é independente das forças internas, permitindo um cálculo direto. Para o Estado II, a profundidade do eixo neutro é calculada de forma iterativa. Por razões numéricas, o programa utiliza a taxa mínima de armadura ρ_min = 10^-4 para ambas as superfícies críticas (superior e inferior), mas apenas com componente de força normal positiva. Isso significa que, na ausência de armadura, é considerada uma área mínima virtual de armadura. Um valor tão pequeno não tem impacto significativo nos resultados (rigidezes).

As propriedades ideais calculadas da seção transversal (referentes à seção de concreto) em uma direção de armadura ф e para o estado de fissuração c são: (a) Momento de inércia em relação ao centroide ideal I_c,ф; (b) Momento de inércia em relação ao centro geométrico da seção I_0,c,ф; (c) Área da seção transversal A_c,ф; (d) Excentricidade do centroide ideal e_c,ф.

1.5. Efeitos de longo prazo

A retração e a fluência são propriedades dependentes do tempo do concreto. De acordo com a EN 1992-1-1, os efeitos de longo prazo devem ser considerados separadamente.

1.5.1. Fluência

Os efeitos da fluência são considerados por uma redução no módulo de elasticidade do concreto E_c, utilizando o coeficiente de fluência efetivo ϕ_eff de acordo com a EN 1992-1-1, equação (7.20):

1.5.2. Retração

Na análise de deflexão de acordo com a EN 1992-1-1, existem dois aspectos que são afetados pelos efeitos de retração.

1.5.2.1. Redução da rigidez do material A rigidez do material em cada direção de armadura φ é reduzida por um chamado coeficiente de influência da retração k_sh,c,φ. Para ambos os estados de fissuração c (fissurado / não fissurado), as forças normais de retração n_sh,c,φ e momentos de flexão m_sh,c,φ são determinados a partir da deformação de retração livre ε_sh:

Fig. 1.1: Forças internas n_sh,ф e m_sh,ф Com essas forças internas de retração, calcula-se a curvatura adicional κ_sh,c,ф no ponto analisado - sem a influência do modelo ao redor. Em seguida, o coeficiente de influência da retração é

O coeficiente k_sh,c,ф é limitado à faixa k_sh,c,ф ∈ (1, 100). Portanto, k_sh,c,ф não pode reduzir a rigidez em mais de 100 vezes (por razões numéricas e físicas). O valor mínimo k_sh,c,ф = 1,0 significa que a influência da retração pode não ser considerada se esta apresentar orientação oposta à curvatura causada pela carga κ_d. Se a retração estiver desativada, o coeficiente k_sh,c,ф = 1,0. O impacto da retração na rigidez de membrana não é considerado.

1.5.2.2. Cálculo do coeficiente de distribuição O segundo impacto da retração refere-se ao cálculo do coeficiente de distribuição (parâmetro de dano) ζ de acordo com a EN 1992-1-1, seção 7.4.3, equação (7.18). O capítulo seguinte descreve o coeficiente de distribuição em detalhe.

1.6. Coeficiente de distribuição

O cálculo do coeficiente de distribuição ζ_d é realizado para a direção de armadura ф. Primeiro, o programa calcula a máxima tensão de tração do concreto σ_max,ф assumindo um comportamento linear-elástico do material. Se os efeitos de longo prazo (fluência ou retração) estiverem ativados, a tensão máxima deve ser calculada duas vezes, caso contrário, apenas uma vez.

Cálculo de curto prazo: Verifica se as fissuras aparecem imediatamente após a carga. Cálculo de longo prazo: Considera o comportamento da fissura com a influência de fluência ou retração no final do período considerado.

Passos de cálculo: Com fluência ativada: Os parâmetros geométricos de curto prazo e a tensão máxima são calculados. Com retração ativada: É necessário apenas recalcular a tensão de curto prazo. Depois, a máxima tensão final σ_max,ф é calculada como o máximo das tensões de longo prazo σ_max,lt,ф e de curto prazo σ_max,st,ф.

O impacto da força de retração na máxima tensão de tração σ_max,ф é considerado pelas forças internas adicionais de retração. O cálculo do coeficiente de distribuição ζ_d,ф depende de se o Tension-Stiffening, de acordo com a EN 1992-1-1, é considerado no cálculo da deformação.

1.6.1. Coeficiente de distribuição ζ_d,ф considerando o Tension-Stiffening

1.6.2. Coeficiente de distribuição ζ_d,ф sem considerar o Tension-Stiffening

1.6.3. Detecção do estado de fissuração

A detecção do estado de fissuração pode ser configurada na configuração de aptidão ao uso (Serviceability Configuration). As seguintes opções estão disponíveis: (a) O estado de fissuração é calculado com base na carga associada; (b) O estado de fissuração é baseado na combinação característica associada (CO) da situação de dimensionamento de SLS; (c) O estado de fissuração é determinado como um envoltório de todas as situações de dimensionamento de SLS; (d) O estado de fissuração é independente da carga.

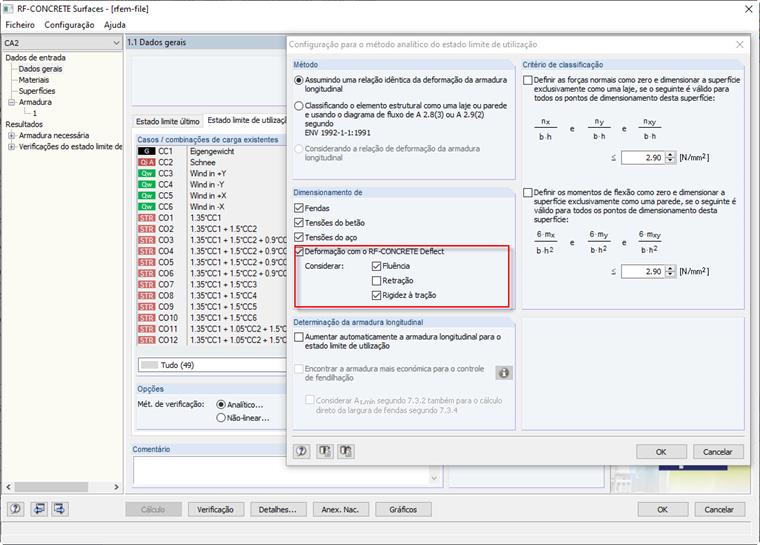
Fig. 1.2: Configuração de aptidão ao uso Se a opção O estado de fissuração é calculado com base na carga associada for selecionada, o estado de fissuração (coeficiente de distribuição ζ_d) será calculado apenas com base na carga atual (combinação de cargas). Se a opção Estado de fissuração baseado na combinação característica associada (CO) da situação de dimensionamento de SLS for selecionada, o coeficiente de distribuição ζ_d será calculado como o máximo de todas as cargas associadas. As cargas associadas podem ser definidas na definição de combinação de cargas.

Fig. 1.3: Cargas associadas Se a opção O estado de fissuração é determinado como um envoltório de todas as situações de dimensionamento de SLS for selecionada, o coeficiente de distribuição ζ_d será calculado como o máximo de todas as situações de dimensionamento. Se a opção Estado de fissuração independente da carga for selecionada, o coeficiente de distribuição é sempre 1,0.

1.6.4. Situações de dimensionamento

Em geral, a deflexão é calculada para cargas quase-permanentes. No entanto, é possível selecionar situações de dimensionamento desejadas (na configuração de aptidão ao uso, opção de atribuição personalizada do tipo de situação de dimensionamento) para as quais a deflexão deve ser calculada. Os seguintes tipos de situações de dimensionamento para aptidão ao uso podem ser selecionados: - Quase-permanente, - Frequente, - Característico. Para cada tipo, pode ser definido um limite para a deflexão (veja Fig. 1.2). Além disso, as situações de dimensionamento desejadas são também definidas para o dimensionamento de concreto.

Fig. 1.4: Ajuste das situações de dimensionamento para o dimensionamento de concreto Para a detecção do estado de fissuração (especialmente na escolha se a detecção é a partir de cargas associadas ou de todas as situações de dimensionamento para aptidão ao uso), a configuração no dimensionamento de concreto é crucial. Em outras palavras: - Se uma situação de dimensionamento estiver desativada na configuração de aptidão ao uso, mas ativada na configuração de dimensionamento de concreto, essa situação de dimensionamento será considerada. - Se uma situação de dimensionamento estiver ativada na configuração de aptidão ao uso, mas desativada na configuração de dimensionamento de concreto, essa situação de dimensionamento não será considerada.

1.7. Propriedades da seção transversal para a análise de deformação

Na matriz de rigidez do material D para a análise de deformação, o programa precisa das propriedades da seção transversal em cada direção de armadura, dependendo do estado de fissuração. Estes são: (a) Momento de inércia em relação ao centroide ideal I_ф; (b) Momento de inércia em relação ao centro geométrico da seção I_0,c; (c) Área da seção transversal ideal A_ф; (d) Excentricidade do centroide ideal e_ф em relação ao centro geométrico. Um encolhimento médio ε_ф e uma curvatura média κ_ф são calculados por interpolação entre o estado fissurado e o não fissurado de acordo com a EN 1992-1-1, equação (7.18):

A deformação no estado não fissurado e no estado fissurado c (Estados I e II) é calculada de acordo com as seguintes equações: As propriedades ideais da seção transversal são calculadas em relação ao centroide ideal da seção. O impacto da retração é considerado pelo fator k_sh,c,ф : Se a força normal for diferente de zero, as propriedades da seção transversal são calculadas em relação ao centro geométrico da seção considerando a excentricidade:

1.8. Matriz de rigidez do material D (Barras)

A rigidez axial EA e a rigidez flexional EI_y,0 são calculadas apenas na direção de armadura ф = 1 (direção da barra), da seguinte forma:

1.9. Matriz de rigidez do material D (Superfícies)

Ao calcular as propriedades da seção transversal, o valor inicial da razão de Poisson ν_init em ambas as direções é reduzido independentemente de acordo com a seguinte equação:

A matriz de rigidez do material é calculada segundo a teoria para superfícies ortotrópicas.

1.9.1. Rigidez flexional - Placas e Cascas

As rigidezes flexionais nas direções de armadura ф são determinadas como segue: Para cascas:

Para placas: O componente não diagonal da matriz de rigidez do material é idêntico para placas e cascas: Para cascas, as diferenças nas rigidezes flexionais devido aos momentos de inércia são compensadas pelos componentes de excentricidade na matriz de rigidez do material.

1.9.2. Rigidez torsional de Placas e Cascas

Os elementos da matriz de rigidez para placas e cascas são calculados da seguinte forma:

1.9.3. Rigidez ao corte de Placas e Cascas

Os elementos da matriz de rigidez para corte não são reduzidos na análise de deformação. Eles são determinados a partir do módulo de cisalhamento G da seção transversal ideal e da altura da seção transversal h. A expressão é idêntica para cascas e placas:

1.9.4. Rigidez de membrana de Cascas

As rigidezes de membrana nas direções de armadura ф são calculadas da seguinte forma:

A parte não diagonal da matriz de rigidez do material é determinada por: A parte de rigidez ao corte é:

1.9.5. Excentricidade – Cascas

Os elementos da matriz de rigidez para a excentricidade do centroide (seção transversal ideal) na direção de armadura ф são calculados como segue:

A parte não diagonal da matriz de rigidez do material é determinada por: O componente de excentricidade para torção é calculado da seguinte forma:

1.9.6. Teste de definição positiva

A positividade definida da matriz de rigidez do material D é testada usando um critério SYLVESTER modificado (considerando blocos de zero). Se a matriz de rigidez D não for definida positivamente, os componentes não diagonais da matriz de rigidez do material são sucessivamente configurados para zero. No caso extremo, apenas os componentes positivos da diagonal principal são mantidos.

1.10. Cálculo das deflexões

As deflexões de um objeto (barra ou superfície) são determinadas usando a matriz de rigidez D pré-calculada. O valor de dimensionamento (Design Ratio) é calculado a partir da deflexão e do limite.

1.10.1. Carga associada

Se uma carga associada for atribuída à carga principal, a deflexão final é calculada como a soma dos valores individuais. A combinação de carga principal é calculada sem propriedades dependentes do tempo (fluência e retração) e, portanto, deve ser de curto prazo (frequente ou característica). A combinação de carga associada, por outro lado, é sempre calculada com propriedades dependentes do tempo e, portanto, deve ser de longo prazo (quase-permanente). Se mais de uma carga associada for atribuída, a carga com o maior valor de deflexão é considerada. A deflexão total é calculada da seguinte forma:

1.11. Diferenças entre o RFEM 5 e o RFEM 6

Cálculo da altura da zona de compressão do concreto No RFEM 5, a altura da zona de compressão do concreto é calculada com base na altura líquida da seção transversal, enquanto no RFEM 6, a altura bruta da seção transversal é utilizada. Esse procedimento garante um cálculo mais rápido e claro, permitindo uma melhor interpretação dos resultados. Com essa simplificação, a precisão do cálculo mantém-se em um nível elevado, de modo que os resultados não apresentem diferenças significativas na prática. O RFEM 6 oferece, assim, uma solução mais eficiente, com resultados precisos constantes.

Coeficiente de distribuição da armadura O coeficiente de distribuição, que descreve a distribuição de tensão ao longo da seção transversal, no RFEM 5 era determinado exclusivamente com base na tensão de longo prazo. Isso significa que apenas a tensão considerada ao longo de um período prolongado era levada em conta. No RFEM 6, a abordagem de cálculo foi desenvolvida de forma a agora considerar o máximo da tensão de longo e curto prazo. Essa mudança garante uma reprodução mais realista das condições efetivas de tensão na seção transversal.