Cálculo directo de deformaciones

método de rigidez efectiva (ESM)

1. Descripción del contexto teórico

Para el análisis de deformaciones en el contexto del diseño de hormigón, se utiliza un método analítico para estructuras 2D y elementos 1D que están sometidos a fuerzas normales y momentos flectores. Este método se basa en la determinación de rigideces efectivas (Método de Rigidez Efectiva) a nivel de sección transversal considerando el estado fisurado, así como efectos de endurecimiento por tensión (Tension Stiffening) y efectos a largo plazo simples (retracción y fluencia).

1.1. Suposiciones básicas de material y geometría

Para el análisis directo de deformaciones en el diseño de hormigón se asume un comportamiento lineal-elástico a compresión y un comportamiento lineal-elástico hasta alcanzar la resistencia a tracción. Estas suposiciones son suficientes para la verificación de la aptitud al servicio. Si los esfuerzos superan la resistencia a compresión del hormigón, el desarrollo de daños se realiza según EN 1992-1-1, sección 7.3.4. El cálculo se basa en un modelo simple isotrópico de mecánica de fractura, definido individualmente para ambas direcciones de refuerzo. Según EN 1992-1-1, se calcula una matriz de rigidez del material efectiva mediante interpolación entre el estado no fisurado (Estado I) y el estado fisurado (Estado II) según sección 7.4.3, ecuación (7.18). Así, se modela el hormigón armado como un material ortótropo, incorporando efectos como el endurecimiento por tensión y efectos a largo plazo simples (retracción y fluencia). El cálculo de las matrices de rigidez del material se implementa para los tipos de modelo 2D-XY (u_z / φ_x / φ_y) y 3D. En el modelo 3D se considera además la influencia de las excentricidades de los centros de gravedad ideales en la matriz de rigidez.

1.2. Fuerzas internas de diseño

Como se describió anteriormente, el cálculo de las rigideces se basa en suposiciones lineal-elásticas. Las fuerzas internas se transforman ortogonalmente a la dirección del refuerzo ф y en ambas superficies s (superior e inferior). Las fuerzas internas obtenidas – momentos flectores m_s,ф y fuerzas normales n_s,ф (los momentos de torsión se eliminan por transformación) – dependen de: (a) Tipo de modelo; (b) Método de cálculo; (c) Criterio de clasificación.

1.3. Superficie crítica

Para determinar la superficie crítica, se considera cada dirección de refuerzo ф por separado. El estado de tensiones se analiza en la superficie inferior (en dirección del eje local +z) y en la superficie superior (en dirección del eje local -z). La superficie con mayor tensión de tracción en el hormigón se considera determinante. Las fuerzas internas en las superficies críticas se denominan n_ф y m_ф.

La fuerza normal n_ф,s, transformada a la dirección de refuerzo ф, tiene el mismo valor para ambas superficies (n_ф = n_ф,superior = n_ф,inferior). Por lo tanto, las fuerzas normales no son relevantes para determinar la superficie crítica; solo se consideran los momentos flectores para encontrar la superficie determinante. Los signos de los momentos flectores m_ф,s se determinan dependiendo de si los momentos causan tracción o compresión en la respectiva superficie. La superficie crítica es la que presenta el mayor momento flector (es decir, la superficie más sometida a tracción).

Para el cálculo de las rigideces, solo se consideran las fuerzas internas n_ф y m_ф en la superficie crítica. Hasta ahora, el término "superficie inferior" se refería al eje local +z. Sin embargo, a partir de ahora "superficie inferior" se refiere al lado determinante de la superficie.

1.4. Propiedades de la sección transversal

Las propiedades de la sección transversal se determinan para ambas direcciones de refuerzo y para ambos estados de sección c (fisurado / no fisurado). Para el Estado I (sección no fisurada) se asume un comportamiento lineal-elástico del hormigón en tracción. Para el Estado II (sección fisurada) no se considera la resistencia a tracción del hormigón.

El cálculo de los parámetros geométricos es independiente de las fuerzas internas para el Estado I, permitiendo un cálculo directo. Para el Estado II, la profundidad del eje neutro se calcula iterativamente. Por razones numéricas, el programa utiliza el porcentaje mínimo de refuerzo ρ_min = 10^-4 para ambas superficies determinantes (superior e inferior), pero solo cuando hay una componente positiva de fuerza normal. Esto significa que, en ausencia de refuerzo, se asume un área de refuerzo virtual mínima. Un valor tan pequeño no tiene un impacto significativo en los resultados (rigideces).

Las propiedades de sección transversal ideales calculadas (referidas a la sección de hormigón) en una dirección de refuerzo ф y para el estado de fisura c son: (a) Momento de inercia respecto al centro de gravedad ideal I_c,ф; (b) Momento de inercia respecto al centro de gravedad geométrico de la sección I_0,c,ф; (c) Área de la sección transversal A_c,ф; (d) Excentricidad del centro de gravedad ideal e_c,ф.

1.5. Efectos a largo plazo

La retracción y la fluencia son propiedades del hormigón que dependen del tiempo. Según EN 1992-1-1, los efectos a largo plazo deben considerarse por separado.

1.5.1. Fluencia

Los efectos de fluencia se consideran mediante una reducción del módulo de elasticidad del hormigón E_c, usando el coeficiente de fluencia efectivo ϕ_eff según EN 1992-1-1, ecuación (7.20):

1.5.2. Retracción

En el cálculo de deflexiones según EN 1992-1-1, hay dos aspectos influenciados por los efectos de retracción.

1.5.2.1. Reducción de la rigidez del material La rigidez del material en cada dirección de refuerzo φ se reduce por el denominado coeficiente de influencia de retracción k_sh,c,φ. Para ambos estados de fisura c (fisurado / no fisurado) se determinan las fuerzas normales de retracción n_sh,c,φ y los momentos flectores m_sh,c,φ a partir de la deformación de retracción libre ε_sh:

Fig. 1.1: Fuerzas internas n_sh,ф y m_sh,ф Con estas fuerzas internas de retracción, se calcula la curvatura adicional κ_sh,c,ф en el punto analizado, sin la influencia del modelo circundante. Posteriormente se calcula el coeficiente de influencia de retracción

El coeficiente k_sh,c,ф está limitado al rango k_sh,c,ф ∈ (1, 100). Por lo tanto, k_sh,c,ф no puede reducir la rigidez en más de 100 veces (por razones numéricas y físicas). El valor mínimo k_sh,c,ф = 1,0 significa que el efecto de la retracción no puede considerarse cuando esta tiene una orientación opuesta a la curvatura κ_d causada por la carga. Si la retracción está desactivada, el coeficiente k_sh,c,ф = 1,0. El efecto de la retracción en la rigidez de membrana no se considera.

1.5.2.2. Cálculo del coeficiente de distribución El segundo efecto de la retracción concierne al cálculo del coeficiente de distribución (parámetro de daño) ζ según EN 1992-1-1, sección 7.4.3, ecuación (7.18). El siguiente capítulo describe en detalle el coeficiente de distribución.

1.6. Coeficiente de distribución

Se presenta el cálculo del coeficiente de distribución ζ_d para la dirección de refuerzo ф. Primero, el programa calcula la tensión máxima de tracción en el hormigón σ_max,ф suponiendo un comportamiento del material lineal-elástico. Si los efectos a largo plazo (fluencia o retracción) están activados, la tensión máxima debe calcularse dos veces; de lo contrario, solo una vez.

Cálculo a corto plazo: Verifica si ocurren fisuras inmediatamente después de la carga. Cálculo a largo plazo: Considera el comportamiento de fisura con la influencia de fluencia o retracción al final del período considerado.

Pasos de cálculo: Si la fluencia está activada: Se calculan parámetros geométricos y tensión máxima a corto plazo. Si la retracción está activada: Solo es necesario recalcular la tensión a corto plazo. Después de esto, se calcula la tensión máxima final σ_max,ф como el máximo entre la tensión a largo plazo σ_max,lt,ф y la tensión a corto plazo σ_max,st,ф.

El efecto de la fuerza de retracción sobre la tensión máxima de tracción σ_max,ф se considera a través de fuerzas internas adicionales de retracción. El cálculo del coeficiente de distribución ζ_d,ф depende de si se considera el endurecimiento por tensión según EN 1992-1-1 en el cálculo de deformaciones.

1.6.1. Coeficiente de distribución ζ_d,ф considerando el endurecimiento por tensión

1.6.2. Coeficiente de distribución ζ_d,ф sin considerar el endurecimiento por tensión

1.6.3. Detección del estado de fisura

La detección del estado de fisura puede configurarse en la configuración de aptitud al servicio (Serviceability Configuration). Se encuentran disponibles las siguientes opciones: (a) El estado de fisura se calcula basado en la carga correspondiente; (b) Estado de fisura basado en la combinación característica correspondiente (CO) de la situación de diseño SLS; (c) Estado de fisura determinado como la envolvente de todas las situaciones de diseño SLS; (d) Estado de fisura independiente de la carga.

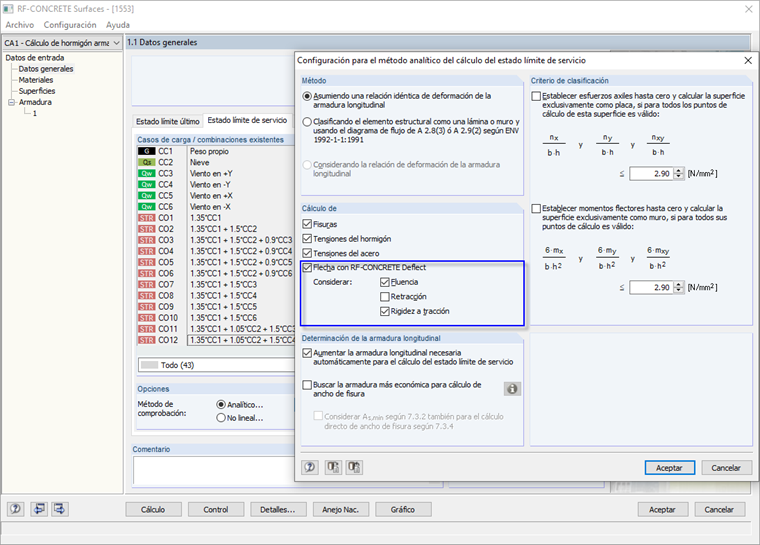
Fig. 1.2: Configuración de aptitud al servicio Si se selecciona la opción El estado de fisura se calcula basado en la carga correspondiente, el estado de fisura (coeficiente de distribución ζ_d) se calcula solo basado en la actual carga (combinación de carga). Si se selecciona la opción Estado de fisura basado en la combinación característica correspondiente (CO) de la situación de diseño SLS, se calcula el coeficiente de distribución ζ_d como el máximo de todas las cargas correspondientes. Las cargas correspondientes pueden definirse en la definición de la combinación de carga.

Fig. 1.3: Cargas correspondientes Si se selecciona la opción Estado de fisura determinado como la envolvente de todas las situaciones de diseño SLS, se calcula el coeficiente de distribución ζ_d como el máximo de todas las situaciones de diseño. Si se selecciona la opción Estado de fisura independiente de la carga, el coeficiente de distribución siempre es 1,0.

1.6.4. Situaciones de diseño

Generalmente, la deflexión se calcula para cargas cuasi permanentes. Sin embargo, es posible seleccionar las situaciones de diseño deseadas (en la configuración de aptitud al servicio, opción Asignación personalizada del tipo de situación de diseño) para las cuales se calculará la deflexión. Se pueden seleccionar los siguientes tipos de situaciones de diseño de aptitud al servicio: - Cuasi permanente, - Frecuente, - Característica. Para cada tipo, se puede establecer un límite para la deflexión (ver Fig. 1.2). Además, las situaciones de diseño deseadas también se establecen para el diseño de hormigón.

Fig. 1.4: Configuración de situaciones de diseño para el diseño de hormigón Para la detección del estado de fisura (especialmente al seleccionar si la detección se hace desde cargas correspondientes o desde todas las situaciones de diseño de aptitud al servicio) es crucial la configuración en el diseño de hormigón. En otras palabras: - Si una situación de diseño está desactivada en la configuración de aptitud al servicio pero activada en la configuración de diseño de hormigón, se considerará la situación de diseño. - Si una situación de diseño está activada en la configuración de aptitud al servicio pero desactivada en la configuración de diseño de hormigón, no se considerará la situación de diseño.

1.7. Propiedades de la sección transversal para el análisis de deformaciones

En la matriz de rigidez del material D para el análisis de deformaciones, el programa necesita las propiedades de la sección transversal en cada dirección de refuerzo, dependiendo del estado de fisura. Estas son: (a) Momento de inercia respecto al centro de gravedad ideal I_ф; (b) Momento de inercia respecto al centro de gravedad geométrico de la sección I_0,c; (c) Área de sección ideal A_ф; (d) Excentricidad del centro de gravedad ideal e_ф respecto al centro de gravedad geométrico. Una deformación media ε_ф y una curvatura media κ_ф se calculan mediante interpolación entre el estado fisurado y no fisurado según EN 1992-1-1, ecuación (7.18):

La deformación en el estado no fisurado y fisurado c (Estado I y II) se calcula con las siguientes ecuaciones: Las propiedades ideales de la sección se calculan respecto al centro de gravedad ideal de la sección. El efecto de la retracción se considera mediante el factor k_sh,c,ф : Si la fuerza normal es diferente de cero, las propiedades de la sección se calculan respecto al centro de gravedad geométrico de la sección considerando la excentricidad:

1.8. Matriz de rigidez del material D (Barras)

La rigidez axial EA y la rigidez a flexión EI_y,0 solo se calculan en la dirección de refuerzo ф = 1 (dirección de la barra) como sigue:

1.9. Matriz de rigidez del material D (Superficies)

En el cálculo de las propiedades de la sección, el valor inicial del coeficiente de Poisson ν_init se reduce de forma independiente en ambas direcciones según la siguiente ecuación:

La matriz de rigidez del material se calcula según la teoría de superficies ortotrópicas.

1.9.1. Rigidez a flexión - Placas y láminas

Las rigideces a flexión en las direcciones de refuerzo ф se determinan como sigue: Para láminas:

Para placas: La componente no diagonal de la matriz de rigidez del material es idéntica para placas y láminas: Para láminas, las diferencias en las rigideces a flexión debido a los momentos de inercia se compensan mediante las componentes de excentricidad en la matriz de rigidez del material.

1.9.2. Rigidez a torsión de placas y láminas

Los elementos de la matriz de rigidez se calculan para placas y láminas como sigue:

1.9.3. Rigidez a cortante de placas y láminas

Los elementos de la matriz de rigidez para cortante no se reducen en el análisis de deformaciones. Se determinan a partir del módulo de corte G de la sección ideal y la altura de la sección h. La expresión es idéntica para láminas y placas:

1.9.4. Rigidez de membrana de láminas

Las rigideces de membrana en las direcciones de refuerzo ф se calculan como sigue:

La parte no diagonal de la matriz de rigidez del material se determina mediante: La proporción de la componente de rigidez a cortante es:

1.9.5. Excentricidad – Láminas

Los elementos de la matriz de rigidez para la excentricidad del centro de gravedad (sección ideal) en la dirección de refuerzo ф se calculan así:

La parte no diagonal de la matriz de rigidez del material se calcula mediante: La componente de excentricidad para torsión se calcula como sigue:

1.9.6. Prueba de positividad definida

Se prueba la positividad definida de la matriz de rigidez del material D mediante un criterio de SYLVESTER modificado (considerando los bloques nulos). Si la matriz de rigidez D no es positiva definida, las componentes no diagonales de la matriz de rigidez del material se reducen sucesivamente a cero. En el caso extremo, solo las componentes positivas de la diagonal principal permanecen.

1.10. Cálculo de deflexiones

Las deflexiones de un objeto (barra o superficie) se determinan mediante el uso de la matriz de rigidez precalculada D. El valor de diseño (Design Ratio) se calcula a partir de la deflexión y el valor límite.

1.10.1. Carga correspondiente

Cuando se asigna una carga correspondiente a la carga principal, la deflexión final se calcula como la suma de los valores individuales. La combinación de carga principal se calcula sin propiedades dependientes del tiempo (fluencia y retracción) y debe ser a corto plazo (frecuente o característica). La combinación de carga correspondiente se calcula siempre con propiedades dependientes del tiempo y debe ser a largo plazo (cuasi permanente). Si hay más de una carga correspondiente asignada, se considera aquella con el valor más alto de deflexión. La deflexión total se calcula como sigue:

1.11 Diferencias entre RFEM 5 y RFEM 6

Cálculo de la altura de la zona comprimida de hormigón En RFEM 5, la altura de la zona comprimida de hormigón se calcula basada en la altura neta de la sección, mientras que en RFEM 6 se utiliza la altura bruta de la sección. Este enfoque proporciona un cálculo más rápido y comprensible, lo que también permite una mejor trazabilidad de los resultados. Esta simplificación mantiene la precisión del cálculo a un nivel alto, por lo que los resultados en la práctica no presentan diferencias significativas. RFEM 6 ofrece así una solución más eficiente manteniendo resultados igualmente precisos.

Coeficiente de distribución del refuerzo El coeficiente de distribución, que describe la distribución de tensiones a lo largo de la sección, se determinó en RFEM 5 exclusivamente en base a la tensión de larga duración. Esto significa que solo se consideraba la tensión que actúa durante un período prolongado. En RFEM 6, el enfoque de cálculo se ha desarrollado para ahora considerar el máximo tanto de la tensión de larga duración como de la tensión a corto plazo. Este cambio proporciona una representación más realista de las condiciones de tensión reales en la sección.