Online manuály RFEM 6 / RSTAB 9 | Posouzení železobetonových konstrukcí

Zpět k online manuálům

415x

005936

Ann-Kathrin Dannwerth, B.Sc.

23.1.2025

Vybrat manuál

Přehled

Addon Posouzení betonových konstrukcí

Základy teorie

Parametry výpočtu

Zadání posouzení

Dimenzování,

Výsledky

Dokumentace

Přímý výpočet deformace

Pomocí metody efektivní tuhosti (ESM)

1. Popis teoretického zázemí

Pro analýzu deformací v rámci betonářského návrhu se používá analytická metoda pro 2D struktury a 1D prvky, které jsou vystaveny normálovým silám a ohybovým momentům. Ta je založena na určení efektivních tuhostí (metoda efektivní tuhosti) na úrovni průřezu s ohledem na stav trhlin a účinky jako tension stiffening a jednoduché dlouhodobé účinky (smršťování a dotvarování).

1.1. Základní materiálové a geometrické předpoklady

Pro přímou analýzu deformací v betonářském návrhu se předpokládá lineárně elastické tlakové chování a lineárně elastické chování až do dosažení pevnosti v tahu. Tyto předpoklady jsou dostatečné pro prokázání použitelnosti. Překročí-li napětí pevnost betonu v tlaku, dochází k rozvoji poškození podle EN 1992-1-1, odstavec 7.3.4.
Výpočet je založen na jednoduchém izotropním modelu lomové mechaniky, který je individuálně definován pro oba směry výztuže. Podle EN 1992-1-1 je efektivní materiálová tuhostní matice vypočítána interpolací mezi neroztrženým stavem (Stav I) a roztrženým stavem (Stav II) podle odstavce 7.4.3, rovnice (7.18). Železobeton je tak modelován jako ortotropní materiál. Zvažují se účinky jako tension stiffening a jednoduché dlouhodobé účinky (smršťování a dotvarování).
Výpočet materiálových tuhostních matic je proveden pro typy modelů 2D-XY (u_z / φ_x / φ_y) a 3D. U 3D modelu se navíc zohledňuje vliv excentricit ideálních těžišť v tuhostní matici.

1.2. Vypočet vnitřních sil

Jak je uvedeno výše, výpočet tuhostí je založen na lineárně elastických předpokladech. Vnitřní síly jsou transformovány ortogonálně ke směru výztuže ф a na oba povrchy s (nahoru a dolů). Získané vnitřní síly – ohybové momenty m_s,ф a normálové síly n_s,ф (torzní momenty se přeměnou eliminují) – závisí na:
(a) typu modelu;
(b) výpočtové metodě;
(c) klasifikačním kritériu.

1.3. Kritický povrch

Pro určení kritického povrchu se každý směr výztuže ф zkoumá samostatně. Napěťový stav se analyzuje na dolním povrchu (ve směru lokální +z-osi) a na horním povrchu (ve směru lokální -z-osi). Povrch s větším betonovým tahem je považován za rozhodující. Vnitřní síly na kritických površích se označují jako n_ф a m_ф.

Normálová síla n_ф,s, transformovaná do směru výztuže ф, má na obou površích stejnou hodnotu (n_ф = n_ф,nahoru = n_ф,dolů). Proto nejsou normálové síly pro určení kritického povrchu relevantní; pro nalezení rozhodujícího povrchu se zvažují pouze ohybové momenty. Znaménka ohybových momentů m_ф,s jsou určována podle toho, zda momenty na daném povrchu způsobují tah nebo tlak. Kritický povrch je ten s větším ohybovým momentem (tedy více namáhaný tahem).

Pro výpočet tuhostí se zohledňují pouze vnitřní síly n_ф a m_ф na kritickém povrchu. Až dosud se termín "dolní povrch" vztahoval na lokální +z-osi. Následně se však "dolní povrch" vztahuje na rozhodující stranu povrchu.

1.4. Vlastnosti průřezu

Vlastnosti průřezu jsou určeny pro oba směry výztuže a pro oba stavy průřezu c (prasklý / bez prasklin). Pro stav I (bez prasklin) se předpokládá lineárně elastické chování betonu na tah. Pro stav II (prasklý průřez) není pevnost v tahu betonu zohledněna.

Výpočet geometrických parametrů je pro stav I nezávislý na vnitřních silách, takže je možný přímý výpočet. Pro stav II se hloubka neutrální osy vypočítává iterativně. Z numerických důvodů program používá minimální stupeň výztuže ρ_min = 10^-4 pro oba důležité povrchy (nahoru a dolů), avšak pouze při kladné složce normálové síly. To znamená, že při absenci výztuže se nastavuje virtuální minimální výztužná plocha. Tak malá hodnota nemá významný vliv na výsledky (tuhosti).

Vypočtené ideální charakteristiky průřezu (vztažené na betonový průřez) v jednom směru výztuže ф a pro stav trhlin c jsou:
(a) Inerční moment k ideálnímu těžišti I_c,ф
(b) Inerční moment k geometrickému těžišti průřezu I_0,c,ф
(c) Plocha průřezu A_c,ф
(d) Excentricita ideálního těžiště e_c,ф

1.5. Dlouhodobé efekty

Smršťování a dotvarování jsou časově závislé vlastnosti betonu. Podle EN 1992-1-1 jsou dlouhodobé efekty uvažovány samostatně.

1.5.1. Dotvarování

Účinky dotvarování jsou zohledněny snížením modulu pružnosti betonu E_c pomocí efektivního koeficientu dotvarování ϕ_eff podle EN 1992-1-1, rovnice

E_{c, eff} = \frac{E_{cm}}{1 + φ}

Účinný modul pružnosti podle k 7.4.3 (5) Rovnice 7.20

1.5.2. Smršťování

Ve výpočtu průhybů podle EN 1992-1-1 jsou dva aspekty, které jsou ovlivněny účinky smršťování.

1.5.2.1. Redukce materiálové tuhosti
Materiálová tuhost v každém směru výztuže φ je snížena tzv. koeficientem vlivu smršťování k_sh,c,φ. Pro oba stavy trhlin c (prasklý / bez prasklin) jsou smrštovací normálové síly n_sh,c,φ a ohybové momenty m_sh,c,φ stanoveny z volné smrštěniny ε_sh

n_{sh, ϕ} = - ε_{sh} \cdot E_{s} (a_{s 1} + a_{s 2})

m_{sh, ϕ} = n_{sh} \cdot e_{sh}

m_sh,φ	Přídavný moment ze smršťování v těžišti ideálního průřezu ve směru výztuže ф
n_sh,φ	Přídavná osová síla způsobená smršťováním ve směru výztuže ф
a_S1	Dolní plocha výztuže
a_S2	Horní plocha výztuže
E_s	Modul pružnosti výztužné ocele
ε_sh	Smyková přetvoření
e_sh	Excentricita sil smršťování (stav I a stav II) z těžiště ideálního průřezu

Přídavná normálová síla a moment v důsledku smršťování ve výztuži

Diagram znázorňující rozložení osových sil Nsh a momentů Msh na konstrukčním prvku.

Analýza vnitřních sil: N_sh a M_sh

Obr. 1.1: Vnitřní síly n_sh,ф a m_sh,ф
S těmito vnitřními silami z smršťování se vypočítá dodatečné zakřivení κ_sh,c,ф v analyzovaném bodě – bez vlivu okolního modelu. Následně se stanoví koeficient vlivu smršťování

k_{sh, c, ϕ} = (κ_{sh, c, ϕ} + κ_{ϕ}) / κ_{ϕ}

κ_ф	Zakřivení vyvolané vnějším zatížením bez vlivu smršťování ve směru výztuže
κ_sh,c,φ	Zakřivení vyvolané smršťováním (a uspořádáním výztuže) bez vlivu dotvarování ve směru výztuže

Zakřivení vyvolané smršťováním (a uspořádání výztuže) bez vlivu dotvarování ve směru výztuže

Koeficient k_sh,c,ф je omezen na rozmezí k_sh,c,ф∈ (1, 100). Tuhost nesmí být redukována o více než 100-násobek (z numerických a fyzikálních důvodů). Minimální hodnota k_sh,c,ф = 1,0 znamená, že vliv smršťování nelze zohlednit, pokud tento má opačnou orientaci k zakřivení způsobenému zatížením κ_d. Pokud je smršťování deaktivováno, odpovídá koeficient k_sh,c,ф = 1,0.
Vliv smršťování na membránovou tuhost není zohledněn.

1.5.2.2. Výpočet distribučního koeficientu
Druhý vliv smršťování se týká výpočtu distribučního koeficientu (poškozovacího parametru) ζ podle EN 1992-1-1, odstavec 7.4.3, rovnice (7.18). Následující kapitola popisuje distribuční koeficient podrobně.

1.6. Distribuční koeficient

Výpočet distribučního koeficientu ζ_d se provádí pro směr výztuže ф. Program nejprve vypočítá maximální betonové tahové napětí σ_max,ф za předpokladu lineárně elastického chování materiálu. Pokud jsou aktivovány dlouhodobé efekty (dotvarování nebo smršťování), musí být maximální napětí vypočítáno dvakrát, jinak pouze jednou.

Krátkodobý výpočet: Ověřuje, zda trhliny vzniknou okamžitě po zatížení.
Dlouhodobý výpočet: Zahrnuje chování v trhlinách s vlivem dotvarování nebo smršťování na konci sledovaného období.

Výpočetní postup:
Při aktivovaném dotvarování: Krátkodobé geometrické parametry a maximální napětí jsou vypočítány.
Při aktivovaném smršťování: Je nutné pouze znovu vypočítat krátkodobé napětí. Poté je konečné maximální napětí σ_max,ф stanoveno jako maximum z dlouhodobého napětí σ_max,lt,ф a krátkodobého napětí σ_max,st,ф

σ_{\max, lt, φ} = \frac{n_{φ} + n_{sh, φ}}{A_{I, φ}} + \frac{m_{φ} - n_{φ} \cdot (z_{I, φ} - h / 2) + m_{sh, I, φ}}{I_{I, φ} \cdot (h - z_{I, φ})}

σ_{\max, st, φ} = \frac{n_{φ}}{A_{I, st, φ}} + \frac{m_{φ} - n_{φ} \cdot (z_{I, st, φ} - h / 2)}{I_{I, st, mo>mrow>ho> φ /mo>/mo>/mo>/mo>} mo>₂/m>mo>/mi>mrow> - z_{I, st, φ})} /mo>)mrow> mrow>σ_{\max, φ} = \max (σ_{\max, st, φ}, σ_{\max, lt, φ})

n_ф	Osová síla vlivem vnějšího zatížení
n_sh,ф	Přídavná osová síla v důsledku smršťování
m_ф	Moment od vnějšího zatížení
m_sh,I,φ	Přídavný moment způsobený smršťováním ve stavu I
h	Výška průřezu
z_I,φ	Vzdálenost středu ideálního průřezu od povrchu betonu v tlaku ve stavu I
A_I,φ	Ideální plocha průřezu ve stavu I
I_I,φ	Ideální moment setrvačnosti ve stavu I
z_I,st,φ	Vzdálenost těžiště ideálního průřezu od povrchu betonu v tlaku ve stavu I ve směru výztuže ф, krátkodobé zatížení
A_I,st,ф	Ideální plocha průřezu ve stavu I ve směru výztuže ф, krátkodobé zatížení
I_I,st,φ	Ideální moment setrvačnosti ve stavu I ve směru výztuže ф, krátkodobé zatížení

Konečné maximální napětí

Vliv smrštovací síly na maximální tahové napětí σ_max,ф je zohledněn pomocí dodatečných vnitřních sil z smršťování. Výpočet distribučního koeficientu ζ_d,ф závisí na tom, zda se při výpočtu deformací uvažuje tension stiffening podle EN 1992-1-1.

1.6.1. Distribuční koeficient ζ_d,ф se zohledněním tension stiffening

Pro σ_{\max, ф} > f_{ctm} : ζ_{d, ϕ} = 1 - β \cdot {(\frac{fctm}{σ_{maxϕ}})}^{n}

a pro σ_{\max, ф} \leq f_{ctm} : ζ_{d, ϕ} = 0

β	Parametr zohledňující dobu působení zatížení
f_ctm	Střední pevnost v tahu
n	= 2 pro EN 1992-1-1

Součinitel distribuce ζ se zohledněním napětí

1.6.2. Distribuční koeficient ζ_d,ф bez zohlednění tension stiffening

= 1.6.3. Detekce stavu trhlin

Nastavení detekce stavu trhlin lze upravit v konfiguraci použitelnosti (Serviceability Configuration). Dostupné jsou následující možnosti:
(a) Stav trhlin se vypočítá na základě příslušného zatížení;
(b) Stav trhlin založený na příslušné charakteristické kombinaci (CO) SLS - posouzení;
(c) Stav trhlin stanoven jako obálka ze všech SLS-posouzení;
(d) Stav trhlin nezávislý na zatížení.

Rozhraní zobrazující nastavení konfigurace pro detekci stavu trhlin s technickými parametry.

Konfigurace mezního stavu použitelnosti | Detekce stavu trhlin

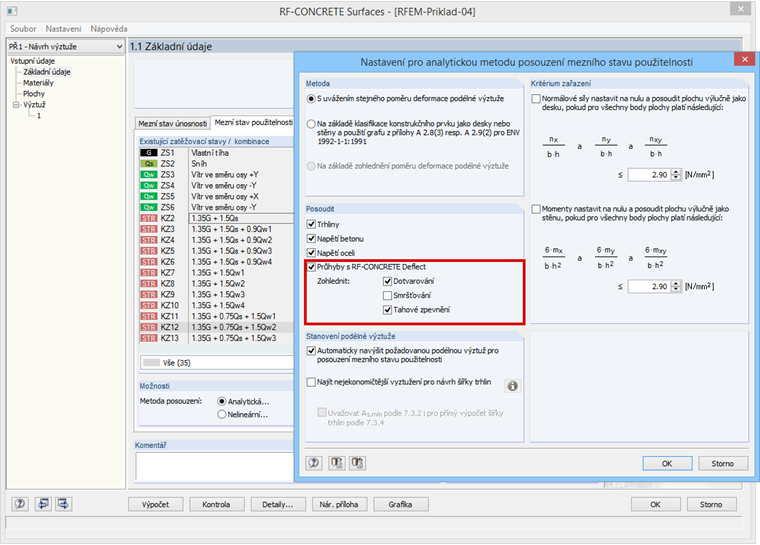
Obr. 1.2: Konfigurace použitelnosti
Pokud je vybrána možnost Stav trhlin se vypočítá na základě příslušného zatížení, stav trhlin (distribuční koeficient ζ_d) se počítá pouze podle aktuálního zatížení (kombinace zatížení).
Pokud je zvolena možnost Stav trhlin založený na příslušné charakteristické kombinaci (CO) SLS - posouzení, distribuční koeficient ζ_d se počítá jako maximum z všech příslušných zatížení. Příslušná zatížení lze stanovit v definici kombinace zatížení.

Odpovídající kombinace zatížení

Obr. 1.3: Příslušná zatížení
Pokud je vybrána možnost Stav trhlin stanoven jako obálka ze všech SLS-posouzení, distribuční koeficient ζ_d se počítá jako maximum ze všech posouzených situací. Pokud je zvolena možnost Stav trhlin nezávislý na zatížení, distribuční koeficient je vždy 1,0.

1.6.4. Posouzené situace

Obecně se průhyb počítá pro kvazistálé zatížení. Je však možné vybrat požadované posouzené situace (v konfiguraci použitelnosti, možnost Vlastní přidělení typu posouzené situace), pro které se má průhyb počítat.
Lze vybrat následující typy posouzení použitelnosti:
- Kvazistálý,
- Často,
- Charakteristický.
Pro každý typ lze stanovit limit průhybu (viz Obr. 1.2). Kromě toho se stanovují požadované posouzené situace i pro betonářský návrh.

Uživatelské rozhraní zobrazující konfigurovatelné parametry navrhování betonových konstrukcí s technickými možnostmi.

Nastavení návrhu pro navrhování betonových konstrukcí

Obr. 1.4: Nastavení posouzených situací pro betonářský návrh
Pro detekci stavu trhlin (zejména při volbě, zda detekce vychází z příslušných zatížení nebo ze všech použitelnostních posouzených situací) je klíčové nastavení v betonářském návrhu.
Jinými slovy:
- Pokud je posouzená situace v konfiguraci použitelnosti deaktivována, ale v nastavení betonářského návrhu aktivována, bude tato posouzená situace zohledněna.
- Pokud je posouzená situace v konfiguraci použitelnosti aktivována, ale v nastavení betonářského návrhu deaktivována, nebude tato posouzená situace zohledněna.

1.7. Charakteristiky průřezu pro analýzu deformací

V materiálové tuhostní matici D pro analýzu deformací program potřebuje charakteristiky průřezu v každém směru výztuže, závislé na stavu trhlin. Tyto jsou:
(a) Inerční moment k ideálnímu těžišti I_ф;
(b) Inerční moment k geometrickému těžišti průřezu I_0,c;
(c) Ideální průřezová plocha A_ф;
(d) Excentricita ideálního těžiště e_ф k geometrickému těžišti.
Střední deformace ε_ф a střední zakřivení κ_ф se vypočítávají interpolací mezi prasklým a bez prasklinových stavem podle EN 1992-1-1, rovnice (7.18)

ε_{ϕ} = ζ_{d, ϕ} \cdot ε_{II, ϕ} + (1 - ζ_{d, ϕ}) \cdot ε_{I, ϕ}

κ_{ϕ} = ζ_{d, ϕ} \cdot κ_{II, ϕ} + (1 - ζ_{d, ϕ}) \cdot κ_{I, ϕ}

Střední přetvoření a střední zakřivení

.
Deformace v bez prasklinovém a prasklém stavu c (stav I a II) se vypočítávají podle následující rovnice

ε_{c, ϕ} = \frac{n_{ϕ}}{E \cdot A_{c, ϕ}}

κ_{c, ϕ} = k_{sh, c, ϕ} \cdot \frac{m_{ϕ} - n_{ϕ} \cdot e_{c, ϕ}}{E \cdot I_{c, ϕ}}

c. deformace ve stavu bez trhlin a ve stavu s trhlinami

.
Ideální charakteristiky průřezu jsou vypočítávány k ideálnímu těžišti průřezu. Vliv smršťování se zohledňuje faktorem k_sh,c,ф

A_{f, ϕ} = \frac{A_{I, ϕ} \cdot A_{II, ϕ}}{ζ_{d, ϕ} \cdot A_{I, ϕ} + (1 - ζ_{d, ϕ}) \cdot A_{II, ϕ}}

I_{f, ϕ} = \frac{I_{I, ϕ} \cdot I_{II, ϕ}}{ζ_{d, ϕ} \cdot I_{I, ϕ} \cdot k_{sh, II, ϕ} + (1 - ζ_{d, ϕ}) \cdot I_{III, ϕ} \cdot k_{sh, I, ϕ}}

Vlastnosti ideálních průřezů s vlivem smršťování

.
Pokud je normálová síla odlišná od nuly, charakteristiky průřezu se vypočítávají k geometrickému těžišti průřezu s ohledem na excentricitu

e_{f, ϕ} = \frac{m_{ϕ} - κ_{ϕ} \cdot E \cdot I_{ϕ}}{n_{ϕ}}

I_{0, f, ϕ} = I_{ϕ} + A_{ϕ} \cdot e_{ϕ}^{2}

Vlastnosti průřezu související s geometrickým středem průřezu pomocí excentrity

1.8. Materiálová tuhostní matice D (pruty)

Axiální tuhost EA a ohybová tuhost EI_y,0 se počítají pouze ve směru výztuže ф = 1 (směr prutu) takto

{EA}_{f} = E_{c, eff} \cdot A_{f}

{EI}_{y, 0, f} = E_{c, eff} \cdot I_{y, 0, f}

Osová tuhost a ohybová tuhost

1.9. Materiálová tuhostní matice D (plochy)

Při výpočtu vlastností průřezu se počáteční hodnota Poissonova poměru ν_init v obou směrech redukuje nezávisle podle následující rovnice

ν_{ϕ} = (1 - ζ_{d, ϕ}) \cdot ν_{init}

Průřezové charakteristiky

.
Materiálová tuhostní matice se vypočítává podle teorie pro ortotropní plochy.

1.9.1. Ohybová tuhost - desky a skořepiny

Ohybové tuhosti ve směru výztuže ф se určují takto:
Pro skořepiny:

D_{d, d} = \frac{I_{0, f, d} \cdot E_{c, eff}}{1 - ν_{1} \cdot ν_{2}}

d	= {1,2} podle směru

Ohybové tuhosti ve směru výztuže ф pro skořepiny

Pro desky:

D_{d, d} = \frac{I_{f, d} \cdot E_{c, eff}}{1 - ν_{1} \cdot ν_{2}}

d	= {1,2} podle směru

Ohybová tuhost ve směrech vyztužení ф pro desky

Ne diagonální složka materiálové tuhostní matice je pro desky a skořepiny identická:

D_{1, 2} = D_{2, 1} = \sqrt{ν_{1} \cdot ν_{2} \cdot D_{1, 1} \cdot D_{2, 2}}

Nediagonální složka matice tuhosti materiálu pro desky a skořepiny

Pro skořepiny se rozdíly v ohybových tuhostech kvůli inerčním momentům vyrovnávají excentricitními složkami v materiálové tuhostní matice.

1.9.2. Torzní tuhost desek a skořepin

Prvky tuhostní matice se pro desky a skořepiny vypočítávají takto

D_{3, 3} = \frac{1 - \sqrt{v_{1} \cdot ν_{2}}}{2} \cdot \sqrt{D_{1, 1} \cdot D_{2, 2}}

Matice tuhosti pro desky a skořepiny

1.9.3. Směrná tuhost desek a skořepin

Prvky tuhostní matice pro směr určují při analýze deformací snížení. Vypočítávají se z modulu smyku G ideálního průřezu a výšky průřezu h. Výraz je pro skořepiny a desky identický

D_{3 + d, 3 + d} = 5 / 6 \cdot G \cdot h

d	= {1,2} podle směru

Matice tuhosti pro smyk z posouvu

1.9.4. Membránová tuhost skořepin

The membrane stiffnesses in the reinforcement directions ф are calculated as follows:

D_{5 + d, 5 + d} = \frac{A_{f, d} \cdot E_{c, eff}}{1 - ν_{1} \cdot ν_{2}}

d	= {1,2} podle směru

Tuhosti membrán ve směrech výztuže

Nediagonální část materiálové tuhostní matice je určena vztahem:

D_{6, 7} = D_{7, 6} = \sqrt{ν_{1} \cdot ν_{2} \cdot D_{6, 6} \cdot D_{7, 7}}

Nediagonální část matice tuhosti materiálu

Podíl na komponentě směrné tuhosti je:

D_{8, 8} = G \cdot h

Složka smykové tuhosti matice tuhosti materiálu

1.9.5. Excentricita – skořepiny

Prvky tuhostní matice pro excentricitu těžiště (ideální průřez) ve směru výztuže ф se vypočítávají takto

D_{d, d + 5} = D_{d + 5, d} = D_{5 + d, 5 + d} \cdot e_{f, d}

d	= {1,2} podle směru

Elementy matice tuhosti pro excentricitu těžiště (ideální průřez) ve směru výztuže

.
Nediagonální část materiálové tuhostní matice je určena vztahem:

D_{1, 7} = \frac{\sqrt{ν_{1} \cdot ν_{2}}}{2} \cdot (e_{f, 1} + e_{f, 2}) \cdot \sqrt{D_{6, 6} \cdot D_{7, 7}}

Nediagonální složka matice tuhosti materiálu

Componenta excentricity pro torzi se vypočítává takto

D_{3, 8} = \frac{1}{2} \cdot G \cdot h \cdot (e_{f, 1} + e_{f, 2})

Složky excentricity pro kroucení

1.9.6. Test na kladnou definitnost

Kladná definitnost materiálové tuhostní matice D je testována upraveným (s ohledem na nulové bloky) SYLVESTROVÝM – Kriteriem.
Pokud tuhostní matice D není kladně definitní, nediagonální složky materiálové tuhostní matice jsou postupně nastaveny na nulu. V krajním případě zůstanou jen kladné složky hlavní diagonály.

1.10. Výpočet průhybů

Průhyby objektu (prut nebo plocha) se určují pomocí předběžně vypočítané tuhostní matice D. Výpočtová hodnota (Design Ratio) se vypočítává z průhybu a limitní hodnoty.

1.10.1. Příslušné zatížení

Pokud je k hlavnímu zatížení přiřazena příslušná zátěž, konečný průhyb se vypočítá jako součet jednotlivých hodnot. Hlavní kombinace zatížení se počítá bez časově závislých vlastností (dotvarování a smršťování) a měla by být tedy krátkodobá (častá nebo charakteristická). Naopak, příslušná kombinace zatížení se vždy počítá s časově závislými vlastnostmi a měla by být tedy dlouhodobá (kvazistálá). Pokud je přiřazeno více než jedno příslušné zatížení, zvažuje se ta , která má největší hodnotu průhybu.
Celkový průhyb se počítá takto

u_{z} = u_{z, tot, QP, lt} + (u_{z, tot, st} - u_{z, tot, QP, st})

u_z,tot,QP,lt	Dlouhodobý průhyb (s dotvarováním a smršťováním) kvazistálého zatížení
u_z,tot,QP,st	Krátkodobé průhyby (bez dotvarování a smršťování) pro kvazistálé zatížení
u_z,tot,st	Krátkodobý průhyb (bez dotvarování a smršťování) současného (častého nebo charakteristického) zatížení

Celkový průhyb

1.11 Rozdíly mezi RFEM 5 a RFEM 6

Výpočet výšky tlakové zóny betonu
V RFEM 5 se výška tlakové zóny betonu počítá na základě netto výšky průřezu, zatímco v RFEM 6 se používá brutto výška průřezu. Tento přístup zajišťuje rychlejší a přehlednější výpočet, který umožňuje lepší sledovatelnost výsledků. Tímto zjednodušením zůstává přesnost výpočtu na vysoké úrovni, takže výsledky v praxi neukazují žádné významné rozdíly. RFEM 6 tedy nabízí efektivnější řešení při zachování přesných výsledků.

Distribuční koeficient výztuže
Distribuční koeficient, který popisuje rozložení napětí přes průřez, byl v RFEM 5 určen výhradně na základě dlouhodobě působícího napětí. To znamená, že bylo zohledněno pouze napětí, které působí po delší dobu. V RFEM 6 byl tento výpočtový přístup dále rozvinut tak, že se nyní zohledňuje maximum jak dlouhodobého, tak krátkodobého napětí. Tato změna zajišťuje realističtější znázornění skutečných napěťových poměrů v průřezu.

Nadřazená kapitola

Omezení deformací

Další odkazy

Model železobetonového nosníku vystaveného tečení a smršťování

Přímá analýza deformací železobetonového nosníku se zohledněním dotvarování a smršťování

Nastavení výpočtu deformací v modulu RF-CONCRETE Deflect

Rozdělovací součinitel ζ při výpočtu deformací železobetonových dílců