返回在线手册

415x

005936

Ann-Kathrin Dannwerth, B.Sc.

2025-01-23

选择手册

概览

混凝土设计模块

基础理论

分析参数

设计规范

设计

结果

文档

直接变形计算

有效刚度法（ESM）

1. 理论背景描述

在混凝土设计的变形分析中，针对承受轴力和弯矩的2D结构和1D元素采用了一种解析方法。该方法基于考虑裂缝状态及张力加强和简单长期效应（收缩和徐变）等效应在截面层面上确定有效刚度（有效刚度法）。

1.1. 基本的材料和几何假设

在混凝土设计的直接变形分析中，假设线性弹性压缩行为以及达到抗拉强度前的线性弹性行为。此类假设对于使用性证明是足够的。如果应力超过混凝土抗压强度，将依据EN 1992-1-1第7.3.4节进行损伤发展。计算基于为两种钢筋方向单独定义的简单各向同性破坏力学模型。根据EN 1992-1-1，依据第7.4.3节公式（7.18）在未开裂状态（状态I）和开裂状态（状态II）之间插值计算有效材料刚度矩阵。因此，钢筋混凝土被建模为正交各向异性材料。需要考虑张力加强、简单长期效应（收缩和徐变）等效应。材料刚度矩阵的计算针对模型类型2D-XY（u_z / φ_x / φ_y）和3D进行。在3D模型中，还考虑了在刚度矩阵中理想重心的偏心影响。

1.2. 设计内部力

如上所述，刚度的计算基于线性 - 弹性假设。内力在钢筋方向ф和两个表面s（上表面和下表面）上进行正交变换。得到的内力 - 弯矩m_s,ф和轴力n_s,ф（通过变换消除扭矩）取决于： (a) 模型类型； (b) 计算方法； (c) 分类标准。

1.3. 临界表面

要确定临界表面，需分别考虑每个钢筋方向ф。在下表面（沿局部+z轴方向）和上表面（沿局部-z轴方向）分析应力状态，具有较大混凝土拉应力的表面视为起决定性作用。关键表面的内力标记为n_ф和m_ф。

已转至钢筋方向ф的轴力n_ф,s在两个表面上的值相同（n_ф = n_{ф, oben} = n_{ф, unten}）。因此，轴力对于确定临界表面并不重要；仅考察弯矩以找出决定性表面。弯矩m_ф,s的符号取决于当前表面产生拉伸或压缩。具有较大弯矩（即更强拉应力）的表面视为临界表面。

刚度的计算仅考虑临界表面的内力n_ф 和 m_ф。至今为止，“下表面”术语指局部+z轴。接下来，“下表面”术语将指表面的决定性侧。

1.4. 横截面特性

针对两种钢筋方向和两种截面状态c（开裂/未开裂）确定横截面特性。状态I（未开裂截面）假设混凝土在拉伸下表现为线性弹性。状态II（开裂截面）不考虑混凝土的拉伸强度。

几何参数的计算在状态I中独立于内力，可以直接计算。对于状态II，中性轴的深度通过迭代计算。由于数值原因，程序在两个决定性表面（上表面和下表面）使用最小钢筋率ρ_min = 10^-4，但仅适用于轴力：正方向的分量。这意即在无钢筋情况下任设虚拟最小钢筋面积。这样的小值对结果（刚度）没有显著影响。

在钢筋方向 ф 和开裂状态 c 下计算的理想截面特性（指混凝土截面）有： (a) 对理想重心的惯性矩 I_c,ф (b) 对截面几何中心的惯性矩 I_0,c,ф (c) 截面面积 A_c,ф (d) 理想重心的偏心 e_c,ф

1.5. 长期效应

收缩和徐变是混凝土的时间依赖特性。根据EN 1992-1-1须分别考虑长期效应。

1.5.1. 徐变

徐变效应通过降低混凝土的弹性模量 E_c 来考虑，使用EN 1992-1-1中的有效徐变系数ϕ_eff公式（7.20）：

E_{c, eff} = \frac{E_{cm}}{1 + φ}

有效模量按照欧洲规范见 7.4.3 (5) 式7.20

1.5.2. 收缩

在按EN 1992-1-1进行的挠度计算中，有两个方面受收缩效应影响。

1.5.2.1. 材料刚度的减少 每个钢筋方向φ的材料刚度通过所谓的收缩影响系数k_sh,c,φ减少。对于两个开裂状态c（开裂/未开裂），根据自由收缩变形ε_sh计算收缩轴力n_sh,c,φ和弯矩m_sh,c,φ：

n_{sh, ϕ} = - ε_{sh} \cdot E_{s} (a_{s 1} + a_{s 2})

m_{sh, ϕ} = n_{sh} \cdot e_{sh}

m_sh,φ	理想截面重心处收缩附加弯矩沿ф配筋方向
n_sh,φ	沿钢筋方向 ф 的收缩轴向力
a_S1	钢筋底部
a_S2	上层配筋
E_s	钢筋的弹性模量
ε_sh	收缩应变
e_sh	收缩力偏心距(状态 I 和状态 II)从理想截面重心

混凝土收缩引起的钢筋附加轴向力和附加弯矩

内力分析：N_sh 和 M_sh

图1.1: 内力n_sh,ф 和 m_sh,ф 用这些由收缩产生的内力来计算分析点的附加曲率κ_sh,c,ф，不考虑周围模型的影响。然后计算收缩影响系数

k_{sh, c, φ} = (κ_{sh, c, φ} + κ_{φ}) / κ_{φ}

κ_ф	外部荷载引起的曲率，混凝土收缩效应方向与钢筋方向垂直。
κ_sh,c,ф	收缩引起的弯曲(以及钢筋布置)不受沿钢筋方向的徐变影响

受混凝土收缩引起的弯曲(与钢筋布置) - 不考虑沿钢筋方向混凝土的徐变

系数k_sh,c,ф被限定在范围k_sh,c,ф∈ (1, 100)内。因此，从数值和物理原因来看不可将k_sh,c,ф用于将刚度减少超过100倍的场合。最小值k_sh,c,ф = 1.0意味着当收缩所产生的曲率方向与负载引起的曲率κ_d方向相反时不可考虑收缩影响。当收缩被禁用时，系数k_sh,c,ф = 1.0。不考虑收缩对膜刚度的影响。

1.5.2.2. 分布系数的计算 收缩影响的第二方面涉及分布系数（损伤参数）ζ的计算，遵循EN 1992-1-1第7.4.3节公式（7.18）。以下章节将详细描述分布系数。

1.6. 分布系数

针对钢筋方向ф计算分布系数ζ_d。首先，程序在假设线性弹性材料行为下计算最大混凝土拉应力σ_max,ф。若长期效应（徐变或收缩）被激活，需计算两次最大应力，否则只需计算一次。

短期计算: 检测裂缝在加载后的即时出现。 长期计算: 考虑至目标时段末的因徐变或收缩影响而产生的裂缝行为。

计算步骤: 若徐变被激活: 计算短期几何参数和最大应力。 若收缩被激活: 只需重新计算短期应力。然后，将最终最大应力σ_max,ф选为长期应力σ_max,lt,ф和短期应力σ_max,st,ф中的最大值。

σ_{\max, lt, φ} = \frac{n_{φ} + n_{sh, φ}}{A_{I, φ}} + \frac{m_{φ} - n_{φ} \cdot (z_{I, φ} - h / 2) + m_{sh, I, φ}}{I_{I, φ} \cdot (h - z_{I, φ})}

σ_{\max, st, φ} = \frac{n_{φ}}{A_{I, st, φ}} + \frac{m_{φ} - n_{φ} \cdot (z_{I, st, φ} - h / 2)}{I_{II, st, φ} \cdot (h - z_{I, st, φ})}

σ_{\max, φ} = \max (σ_{\max, st, φ}, σ_{\max, lt, φ})

n_ф	由于外部荷载引起的轴向力
n_sh,ф	收缩引起的附加轴向力
m_ф	外荷载引起的弯矩
m_sh,I,ф	I 类收缩引起的附加弯矩
h	截面深度
z_I,ф	理想截面重心到状态 I 下受压混凝土表面的距离
A_I,ф	理想截面面积
I_I,ф	阶段 I 理想惯性矩
z_I,st,ф	理想截面的重心到压缩区混凝土表面的距离（配筋方向 ф，短期荷载）
A_I,st,φ	方向 ф 的理想截面面积在受短期荷载作用时的状态 I
I_I,st,ф	短期加载下沿配筋方向 f 的理想惯性矩

最终最大应力

对最大拉应力σ_max,ф的收缩影响通过收缩产生的附加内力进行考虑。分布系数ζ_d,ф的计算受限于是否在变形计算中依据EN 1992-1-1考虑了张力加强。

1.6.1. 考虑张力加强的分布系数ζ_d,ф

当 σ_{\max, ф} > f_{ctm} : ζ_{d, ϕ} = 1 - β \cdot {(\frac{fctm}{σ_{maxϕ}})}^{n}

当 σ_{\max, ф} \leq f_{ctm} : ζ_{d, ϕ} = 0

β	考虑荷载持续时间的参数
f_ctm	平均抗拉强度
n	= 2 针对 EN 1992-1-1

考虑拉伸刚化的分配系数 ζ

1.6.2. 忽略张力加强的分布系数ζ_d,ф

1.6.3. 裂缝状态识别

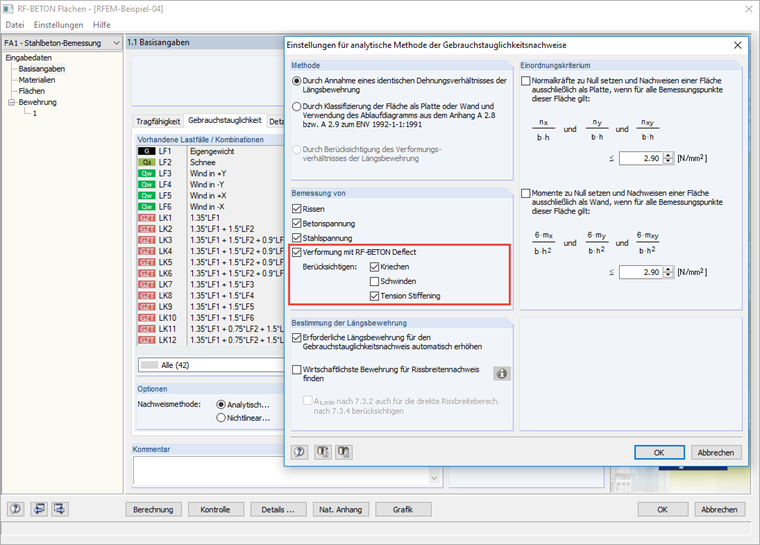
在使用性配置中可以设定裂缝状态的识别。可选选项为： (a) 根据相关负载计算裂缝状态； (b) 基于SLS设计情况的相关特征组合（CO）检测裂缝状态； (c) 通过所有SLS设计情况的包络来判定裂缝状态； (d) 不考虑负载判断裂缝状态。

正常使用极限状态配置 | 裂缝状态检测

图1.2: 使用性配置当选择选项 根据相关负载计算裂缝状态 时，裂缝状态（分布系数ζ_d）仅基于当前负载（荷载组合）计算。当选择选项 基于SLS设计情况的相关特征组合（CO）检测裂缝状态 时，将所有相关负载取其最大值计算分布系数ζ_d。可在荷载组合定义中设定相关负载。

对应的荷载组合

图1.3: 相关负载选择选项 通过所有SLS设计情况的包络来判定裂缝状态 时，分布系数ζ_d是各设计情况的最大值。选择选项 不考虑负载判断裂缝状态 时，分布系数恒为1.0。

1.6.4. 设计情况

通常，基于准永久负载计算挠度。然而，可以选择期望的设计情况（在使用性配置中，选项用户自定义设计情况类型分配），以计算挠度。可选的使用性设计情况类型为： - 准永久， - 频繁， - 特征值。对于每种类型可以设定挠度的限值（参见 图1.2）。此外，期望的设计情况也将用于混凝土设计。

Design Settings for Concrete Design

图1.4: 设置混凝土设计的设计情况裂缝状态的识别（特别是在选择依据相关负载或仅依据所有使用性设计情况的识别）中，混凝土设计的设置是决定性的。换句话说： - 当使用性配置中设计情况被禁用，但在混凝土设计设置下启用时，则考虑该设计情况。 - 当使用性配置中设计情况启用，而在混凝土设计设置下禁用时，则不考虑该设计情况。

1.7. 变形分析的截面特性

在进行变形分析所需的材料刚度矩阵D中，程序需要每个钢筋方向的截面特性，依赖于裂缝状态。这些特性为： (a) 对理想重心的惯性矩 I_ф; (b) 对截面几何中心的惯性矩 I_0,c; (c) 理想截面面积 A_ф; (d) 理想重心与几何中心的偏心 e_ф。平均应变ε_ф和平均曲率κ_ф通过在开裂和未开裂状态之间插值依照EN 1992-1-1公式（7.18）计算：

ε_{ϕ} = ζ_{d, ϕ} \cdot ε_{II, ϕ} + (1 - ζ_{d, ϕ}) \cdot ε_{I, ϕ}

κ_{ϕ} = ζ_{d, ϕ} \cdot κ_{II, ϕ} + (1 - ζ_{d, ϕ}) \cdot κ_{I, ϕ}

平均应变和平均曲率

未开裂和开裂状态c（状态I和II）的变形通过以下公式计算：

ε_{c, ϕ} = \frac{n_{ϕ}}{E \cdot A_{c, ϕ}}

κ_{c, ϕ} = k_{sh, c, ϕ} \cdot \frac{m_{ϕ} - n_{ϕ} \cdot e_{c, ϕ}}{E \cdot I_{c, ϕ}}

未开裂和开裂状态下的变形 c

理想截面特性根据截面的理想重心计算。通过系数k_sh,c,ф考虑收缩的影响：

A_{f, ϕ} = \frac{A_{I, ϕ} \cdot A_{II, ϕ}}{ζ_{d, ϕ} \cdot A_{I, ϕ} + (1 - ζ_{d, ϕ}) \cdot A_{II, ϕ}}

I_{f, ϕ} = \frac{I_{I, ϕ} \cdot I_{III, ϕ}}{ζ_{d, ϕ} \cdot I_{II, ϕ} \cdot k_{sh, II, ϕ} + (1 - ζ_{d, ϕ}) \cdot I_{III, ϕ} \cdot k_{sh, I, ϕ}}

受收缩影响的理想截面特性

当轴向力非零时，通过考虑偏心计算截面特性到几何中心：

e_{f, ϕ} = \frac{m_{ϕ} - κ_{ϕ} \cdot E \cdot I_{ϕ}}{n_{ϕ}}

I_{0, f, ϕ} = I_{ϕ} + A_{ϕ} \cdot e_{ϕ}^{2}

利用偏心与截面几何中心相关的截面属性

1.8. 材料刚度矩阵D（杆件）

仅在钢筋方向ф = 1（杆件方向）中计算轴向刚度EA和弯曲刚度EI_y,0：

{EA}_{f} = E_{c, eff} \cdot A_{f}

{EI}_{y, 0, f} = E_{c, eff} \cdot I_{y, 0, f}

轴向刚度和抗弯刚度

1.9. 材料刚度矩阵D（面）

在截面特性计算中，起始泊松比ν_init按以下公式分别在两个方向上减少：

ν_{ϕ} = (1 - ζ_{d, ϕ}) \cdot ν_{init}

截面属性

依据正交面理论计算材料刚度矩阵。

1.9.1. 弯曲刚度 - 板和壳

在钢筋方向ф的弯曲刚度按如下确定：对于壳：

粘滞风阻尼系数

d	= {1,2} 根据方向

壳体在配筋方向的抗弯刚度 ф

对于板：

D_{d, d} = \frac{I_{f, d} \cdot E_{c, eff}}{1 - ν_{1} \cdot ν_{2}}

d	= {1,2} 按照方向

板的钢筋方向的抗弯刚度 ф

板和壳材料刚度矩阵的非对角成分一致：

D_{1, 2} = D_{2, 1} = \sqrt{ν_{1} \cdot ν_{2} \cdot D_{1, 1} \cdot D_{2, 2}}

板壳材料刚度矩阵的非对角线成分

对壳来说因偏心成分在材料刚度矩阵中平衡惯性矩产生的弯曲刚度差异。

1.9.2. 板和壳的扭转刚度

刚度矩阵的成分对于板和壳计算如下：

D_{3, 3} = \frac{1 - \sqrt{v_{1} \cdot ν_{2}}}{2} \cdot \sqrt{D_{1, 1} \cdot D_{2, 2}}

板和壳的刚度矩阵

1.9.3. 板和壳的剪切刚度

没有减少用以进行变形分析的剪切刚度矩阵成分。由理想截面剪切模量G和截面高度h计算。该表达式对于壳和板一致：

D_{3 + d, 3 + d} = 5 / 6 \cdot G \cdot h

d	= {1,2} 根据方向

剪切刚度矩阵

1.9.4. 壳的膜刚度

在钢筋方向ф的膜刚度按如下计算：

D_{5 + d, 5 + d} = \frac{A_{f, d} \cdot E_{c, eff}}{1 - ν_{1} \cdot ν_{2}}

d	= {1,2} 按方向

配筋方向膜刚度

计算非对角成分的材料刚度矩阵依据：

D_{6, 7} = D_{7, 6} = \sqrt{ν_{1} \cdot ν_{2} \cdot D_{6, 6} \cdot D_{7, 7}}

材料刚度矩阵的非对角线部分

剪切刚度成分的比例为：

D_{8, 8} = G \cdot h

材料刚度矩阵的剪切刚度部分

1.9.5. 偏心——壳

壳在钢筋方向ф的偏心理想截面（理想截面重心的）成分按如下计算：

D_{d, d + 5} = D_{d + 5, d} = D_{5 + d, 5 + d} \cdot e_{f, d}

d	= {1,2} 按照方向

钢筋方向的理想截面的重心偏心刚度矩阵的元素

计算材料刚度矩阵的非对角成分依据：

D_{1, 7} = \frac{\sqrt{ν_{1} \cdot ν_{2}}}{2} \cdot (e_{f, 1} + e_{f, 2}) \cdot \sqrt{D_{6, 6} \cdot D_{7, 7}}

材料刚度矩阵的非对角分量

扭转的偏心成分计算为：

D_{3, 8} = \frac{1}{2} \cdot G \cdot h \cdot (e_{f, 1} + e_{f, 2})

扭转作用的偏心分量

1.9.6. 正定性测试

通过考虑零块的修正SYLVESTER'S准则测试材料刚度矩阵D的正定性。如果刚度矩阵D非正定，则逐步将材料刚度矩阵的非对角成分置为零。在极端情况下，只保留主对角线上的正成分。

1.10. 挠度计算

物体（杆或面）的挠度通过预先计算的刚度矩阵D确定。设计比率（Design Ratio）通过挠度和限值计算得出。

1.10.1. 相关负载

如果为主负载分配了相关负载，最终挠度作为单个值的和计算。主要荷载组合因不包含时间依赖性特性（徐变和收缩）需为短期（频繁或特征值）组合。在这种情况下，相关的荷载组合总通过时间依赖特性计算，总因此为长期（准永久）组合。如分配的多个相关负载，取挠度最高者。总体挠度按如下计算：

u_{z} = u_{z, tot, QP, lt} + (u_{z, tot, st} - u_{z, tot, QP, st})

u_z,tot,QP,lt	准永久荷载的长期挠度(考虑徐变和收缩)
u_z,tot,QP,st	拟永久荷载的短期挠度（不考虑徐变和收缩）
u_z,tot,st	当前(频率或特征)荷载的短期挠度(无徐变和收缩)

总挠度

1.11. RFEM 5 和 RFEM 6 的区别

混凝土压区高度的计算 在RFEM 5中，混凝土压区的高度依据净截面高度计算，而在RFEM 6中采用的是毛截面高度。这一过程保证了更快速和清晰的计算，并且使结果更易于理解。由于这一简化，计算精度仍维持在高水平，因此在实践中计算结果不会出现显著差异。RFEM 6因此提供了一种效率更高而精确度保持不变的解决方案。

钢筋的分布系数 描述截面上的应力分布的分布系数在RFEM 5中仅基于长期作用应力确定。这意味着只考虑了作用时间较长的应力。在RFEM 6中，计算方法得到改进，现在同时考虑长期应力和短期应力的最大值。该更改保证了截面上实际应力状况的更真实反映。

上级章节

变形限制