Bezpośrednie obliczanie odkształceń

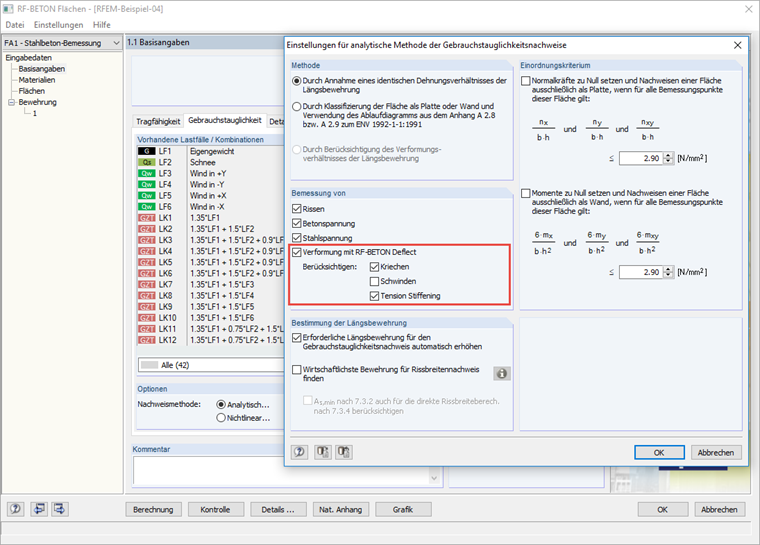
za pomocą metody efektywnej sztywności (ESM)

1. Opis teoretycznego tła

Do analizy odkształceń w ramach projektowania betonu stosuje się analityczną metodę dla struktur 2D i elementów 1D, które są poddane naprężeniom normalnym i momentom zginającym. Opiera się ona na wyznaczeniu efektywnych sztywności (metoda efektywnej sztywności) na poziomie przekroju, uwzględniając stan zarysowania oraz efekty takie jak sztywność naprężenia (Tension Stiffening) i proste efekty długoterminowe (skurcz i pełzanie).

1.1. Podstawowe założenia materiałowe i geometryczne

Do bezpośredniej analizy odkształceń w projektowaniu betonu przyjmuje się liniowo-sprężyste zachowanie w przypadku ściskania oraz liniowo-sprężyste zachowanie do osiągnięcia wytrzymałości na rozciąganie. Takie założenia są wystarczające do zapewnienia przydatności użytkowej. Jeśli naprężenia przekroczą wytrzymałość betonu na ściskanie, rozwój uszkodzeń następuje zgodnie z EN 1992-1-1, Sekcja 7.3.4. Obliczenia opierają się na prostym izotropowym modelu mechaniki zniszczenia, zdefiniowanym indywidualnie dla dwóch kierunków zbrojenia. Zgodnie z EN 1992-1-1, efektywna matryca sztywności materiału jest obliczana przez interpolację między stanem niezarysowanym (Stan I) i stanem zarysowanym (Stan II) zgodnie z Sekcją 7.4.3, równanie (7.18). W ten sposób beton zbrojony jest modelowany jako materiał ortotropowy. Uwzględnia się takie efekty jak sztywność naprężenia oraz proste efekty długoterminowe (skurcz i pełzanie). Obliczenia matryc sztywności materiału są realizowane dla typów modeli 2D-XY (u_z / φ_x / φ_y) oraz 3D. W modelu 3D dodatkowo uwzględniany jest wpływ ekscentryczności idealnych środków ciężkości w matrycy sztywności.

1.2. Wewętrzne siły obliczeniowe

Jak opisano powyżej, obliczenia sztywności opierają się na liniowych - sprężystych założeniach. Wewnętrzne siły są przekształcane ortogonalnie do kierunku zbrojenia φ i dla obu powierzchni s (górnej i dolnej). Otrzymane wewnętrzne siły - momenty zginające m_s,φ i siły normalne n_s,φ (momenty skręcające są eliminowane poprzez transformację) - zależą od: (a) Typu modelu; (b) Metody obliczenia; (c) Kryterium klasyfikacji.

1.3. Krytyczna powierzchnia

Aby określić krytyczną powierzchnię, każda kierunek zbrojenia φ jest rozpatrywany osobno. Stan naprężenia jest analizowany na dolnej powierzchni (w kierunku lokalnej osi +z) oraz górnej powierzchni (w kierunku lokalnej osi -z). Powierzchnia z większym naprężeniem betonu rozciąganego jest uważana za decydującą. Wewnętrzne siły na krytycznych powierzchniach są oznaczane jako n_φ i m_φ.

Siła normalna n_φ,s, która została przetransformowana do kierunku zbrojenia φ, ma dla obu powierzchni tę samą wartość (n_φ = n_φ,góra = n_φ,dół). Dlatego siły normalne nie są istotne dla określenia krytycznej powierzchni; tylko momenty zginające są rozpatrywane, aby znaleźć decydującą powierzchnię. Znaki momentów zginających m_φ,s są określane w zależności od tego, czy momenty powodują naprężenie czy ściskanie na danej powierzchni. Krytyczna powierzchnia to ta z większym momentem zginającym (czyli bardziej naprężona powierzchnia).

Do obliczeń sztywności uwzględnia się tylko wewnętrzne siły n_φ i m_φ na krytycznej powierzchni. Dotychczas termin "dolna powierzchnia" odnosił się do lokalnej osi +z. W dalszej części "dolna powierzchnia" odnosi się jednak do decydującej strony powierzchni.

1.4. Właściwości przekroju

Właściwości przekroju są określane dla obu kierunków zbrojenia oraz dla obu stanów przekroju c (zarysowany / niezarysowany). Dla Stanu I (niezarysowany przekrój) przyjmuje się liniowo-sprężyste zachowanie betonu w przypadku naprężenia rozciągającego. Dla Stanu II (zarysowany przekrój) nie uwzględnia się wytrzymałości na rozciąganie betonu.

Obliczenia parametrów geometrycznych dla Stanu I są niezależne od wewnętrznych sił, co pozwala na bezpośrednie obliczenie. Dla Stanu II głębokość neutralnej osi jest obliczana iteracyjnie. Z przyczyn numerycznych, program używa minimalnego stopnia zbrojenia ρ_min = 10^-4 dla obu decydujących powierzchni (górna i dolna), ale tylko przy dodatniej wartości sił normalnych. Oznacza to, że przy braku zbrojenia przyjmuje się wirtualną minimalną powierzchnię zbrojeniową. Tak mała wartość nie ma znaczącego wpływu na wyniki (sztywność).

Obliczone idealne właściwości przekroju (odniesione do przekroju betonowego) w kierunku zbrojenia φ i dla stanu rysy c są: (a) Moment bezwładności do idealnego środka ciężkości I_c,φ (b) Moment bezwładności do geometrycznego środka ciężkości przekroju I_0,c,φ (c) Powierzchnia przekroju A_c,φ (d) Ekscentryczność idealnego środka ciężkości e_c,φ

1.5. Efekty długoterminowe

Skurcz i pełzanie to właściwości betonu zależne od czasu. Zgodnie z EN 1992-1-1 efekty długoterminowe są uwzględniane osobno.

1.5.1. Pełzanie

Efekty pełzania są uwzględniane poprzez redukcję modułu sprężystości betonu E_c, gdzie skuteczny współczynnik pełzania ϕ_eff jest stosowany zgodnie z EN 1992-1-1, równanie (7.20):

1.5.2. Skurcz

W obliczeniach ugięcia zgodnie z EN 1992-1-1 istnieją dwa aspekty, które są wpływane przez efekty skurczu.

1.5.2.1. Redukcja sztywności materiału Sztywność materiału w każdym kierunku zbrojenia φ jest redukowana przez tzw. współczynnik wpływu skurczu k_sh,c,φ. Dla obu stanów rysy c (zarysowany / niezarysowany) skurczowe siły normalne n_sh,c,φ i momenty m_sh,c,φ są określane z wolnej deformacji skurczowej ε_sh:

Rys. 1.1: Wewnętrzne siły n_sh,φ i m_sh,φ Na podstawie tych wewnętrznych sił z tytułu skurczu obliczana jest dodatkowa krzywizna κ_sh,c,φ w analizowanym punkcie - bez wpływu modelu otoczenia. Następnie jest obliczany współczynnik wpływu skurczu

Współczynnik k_sh,c,φ jest ograniczony do zakresu k_sh,c,φ ∈ (1, 100). Oznacza to, że k_sh,c,φ nie może zredukować sztywności o więcej niż 100-krotnie (z przyczyn numerycznych i fizycznych). Minimalna wartość k_sh,c,φ = 1,0 oznacza, że wpływ skurczu nie może być brany pod uwagę, jeśli ma przeciwną orientację do krzywizny wzbudzonej przez obciążenie κ_d. Gdy skurcz jest dezaktywowany, współczynnik k_sh,c,φ = 1,0. Wpływ skurczu na sztywność membrany nie jest brany pod uwagę.

1.5.2.2. Obliczenia współczynnika dystrybucji Drugi wpływ skurczu dotyczy obliczeń współczynnika dystrybucji (parametr szkody) ζ zgodnie z EN 1992-1-1, Sekcja 7.4.3, równanie (7.18). Niniejszy rozdział szczegółowo opisuje współczynnik dystrybucji.

1.6. Współczynnik dystrybucji

Obliczenia współczynnika dystrybucji ζ_d są przedstawione dla kierunku zbrojenia φ. Najpierw program oblicza maksymalne naprężenie w rozciąganiu betonu σ_max,φ przy założeniu liniowo-sprężystego zachowania materiału. Jeśli efekty długoterminowe (pełzanie lub skurcz) są aktywowane, maksymalne naprężenie należy obliczać dwukrotnie, w przeciwieństwie do jednokrotnych obliczeń, gdy są wyłączone.

Obliczenia krótkoterminowe: Sprawdza, czy pęknięcia pojawiają się bezpośrednio po obciążeniu. Obliczenia długoterminowe: Uwzględnia zachowanie zarysowania pod wpływem pełzania lub skurczu na koniec rozważanego okresu czasu.

Kroki obliczeń: Przy włączonym pełzaniu: Oblicza się parametry geometryczne krótkoterminowe oraz maksymalne naprężenie. Przy włączonym skurczu: Konieczne jest tylko ponowne obliczenie naprężenia krótkoterminowego. Następnie maksymalne naprężenie σ_max,φ określa się jako maksimum spośród naprężenia długoterminowego σ_max,lt,φ oraz naprężenia krótkoterminowego σ_max,st,φ.

Wpływ skurczu na maksymalne napięcie rozciągania σ_max,φ uwzględnia dodatkowe wewnętrzne siły związane ze skurczem. Obliczenia współczynnika dystrybucji ζ_d,φ zależą od tego, czy sztywność naprężenia jest uwzględniana w obliczeniach odkształceń zgodnie z EN 1992-1-1.

1.6.1. Współczynnik dystrybucji ζ_d,φ uwzględniający sztywność naprężenia

1.6.2. Współczynnik dystrybucji ζ_d,φ bez uwzględnienia sztywności naprężenia

1.6.3. Rozpoznanie stanu zarysowania

Rozpoznanie stanu zarysowania można ustawić w konfiguracji przydatności do użytkowania (Serviceability Configuration). Dostępne są następujące opcje: (a) Stan zarysowania jest obliczany na podstawie odpowiedniego obciążenia; (b) Stan zarysowania na podstawie odpowiedniej charakterystycznej kombinacji (CO) sytuacji obliczeniowej SLS; (c) Stan zarysowania jako otoczka ze wszystkich sytuacji obliczeniowych SLS; (d) Stan zarysowania niezależnie od obciążenia.

Rys. 1.2: Konfiguracja przydatności do użytkowania Jeśli wybrana jest opcja Stan zarysowania jest obliczany na podstawie odpowiedniego obciążenia, stan zarysowania (współczynnik dystrybucji ζ_d) jest obliczany tylko na podstawie bieżącego obciążenia (kombinacji obciążeń). Jeśli wybrana jest opcja Stan zarysowania na podstawie odpowiedniej charakterystycznej kombinacji (CO) sytuacji obliczeniowej SLS, współczynnik dystrybucji ζ_d jest obliczany jako maksimum z wszystkich odpowiednich obciążeń. Odpowiednie obciążenia można ustalić w definicji kombinacji obciążeń.

Rys. 1.3: Odpowiednie obciążenia Jeśli wybrana jest opcja Stan zarysowania jako otoczka ze wszystkich sytuacji obliczeniowych SLS, współczynnik dystrybucji ζ_d jest obliczany jako maksimum ze wszystkich sytuacji obliczeniowych. Jeśli wybrana zostanie opcja Stan zarysowania niezależnie od obciążenia, współczynnik dystrybucji wynosi zawsze 1,0.

1.6.4. Sytuacje obliczeniowe

Z reguły ugięcie jest obliczane dla obciążeń quasi-stałych. Jednakże możliwe jest wybranie żądanych sytuacji obliczeniowych (w konfiguracji przydatności do użytkowania, opcja użytkownika Dołączanie sytuacji obliczeniowej typu), dla których ugięcie ma być obliczone. Dostępne są następujące rodzaje sytuacji obliczeniowych przydatności do użytkowania: - Quasi-stała, - Częsta, - Charakterystyczna. Dla każdego typu można ustalić graniczną wartość ugięcia (zob. Rys. 1.2). Ponadto żądane sytuacje obliczeniowe są również ustalane dla zbrojenia betonu.

Rys. 1.4: Ustawienie sytuacji obliczeniowych dla projektowania betonu Ustawienie w projektowaniu betonu jest kluczowe dla rozpoznania stanu zarysowania (zwłaszcza w przypadku wyboru, czy rozpoznanie ma być z obciążeń związanych czy ze wszystkich sytuacji obliczeniowych przydatności do użytkowania). Innymi słowy: - Jeśli sytuacja obliczeniowa jest wyłączona w konfiguracji przydatności do użytkowania, ale aktywowana w ustawieniu projektowania betonu, ta sytuacja obliczeniowa jest brana pod uwagę. - Jeśli sytuacja obliczeniowa jest aktywna w konfiguracji przydatności do użytkowania, ale dezaktywowana w ustawieniu projektowania betonu, ta sytuacja obliczeniowa nie jest uwzględniana.

1.7. Właściwości przekroju dla analizy odkształceń

W matrycy sztywności materiału D do analizy odkształceń program potrzebuje właściwości przekroju w każdym kierunku zbrojenia, odpowiednio do stanu zarysowania. Są to: (a) Moment bezwładności do idealnego środka ciężkości I_φ; (b) Moment bezwładności do geometrycznego środka ciężkości przekroju I_0,c; (c) Idealna powierzchnia przekroju A_φ; (d) Ekscentryczność idealnego środka ciężkości e_φ do geometrycznego środka ciężkości. Średnie odkształcenie ε_φ oraz średnia krzywizna κ_φ są obliczane przez interpolację między stanem zarysowanym i niezarysowanym zgodnie z EN 1992-1-1, równanie (7.18):

Odkształcenie w stanie niezarysowanym i zarysowanym c (Stan I i II) jest obliczane zgodnie z następującymi równaniami: Idealne właściwości przekroju są obliczane do idealnego środka ciężkości przekroju. Wpływ skurczu uwzględnia się przez współczynnik k_sh,c,φ : Jeśli siła normalna jest różna od zera, właściwości przekroju są obliczane do geometrycznego środka ciężkości przekroju, uwzględniając ekscentryczność:

1.8. Matryca sztywności materiału D (pręty)

Sztywność osiowa EA oraz sztywność zginająca EI_y,0 są obliczane tylko w kierunku zbrojenia φ = 1 (kierunek pręta) według następującego wzoru:

1.9. Matryca sztywności materiału D (powierzchnie)

Podczas obliczania właściwości przekroju, początkowa wartość współczynnika Poissona ν_init jest zmniejszana w obu kierunkach zgodnie z następującym równaniem:

Matryca sztywności materiału jest obliczana zgodnie z teorią dla powierzchni ortotropowych.

1.9.1. Sztywność zginania - płyt i powłok

Sztywności zginania w kierunkach zbrojenia φ są określane w następujący sposób: Dla powłok:

Dla płyt: Niediagonalny składnik matrycy sztywności materiału jest identyczny dla płyt i powłok: Dla powłok różnice w sztywności zginania ze względu na momenty bezwładności są równoważone przez składniki ekscentryczności w matrycy sztywności materiału.

1.9.2. Sztywność skrętna płyt i powłok

Elementy matrycy sztywności są obliczane dla płyt i powłok w następujący sposób:

1.9.3. Sztywność ścinania płyt i powłok

Elementy matrycy sztywności dla ścinania w analizie odkształceń nie są redukowane. Są one określane z modułu sprężystości ścinania G przekroju idealnego oraz wysokości przekroju h. Wyrażenie to jest identyczne dla powłok i płyt:

1.9.4. Sztywność membrany powłok

Sztywności membranowe w kierunkach zbrojenia φ są obliczane w następujący sposób:

Niediagonalny składnik matrycy sztywności materiału jest określany przez: Składnik sztywności ścinającej jest następujący:

1.9.5. Ekscentryczność – powłoki

Elementy matrycy sztywności dla ekscentryczności środka ciężkości (idealny przekrój) w kierunku zbrojenia φ są określane w następujący sposób:

Niediagonalny składnik matrycy sztywności materiału jest określany przez: Składnik ekscentryczności dla siły skrętnej jest obliczany w następujący sposób:

1.9.6. Test na dodatnią określoność

Dodatnia określoność matrycy sztywności materiału D jest testowana przy użyciu zmodyfikowanego (uwzględniając bloki zerowe) kryterium SYLWESTRA. Jeśli matryca sztywności D nie jest dodatnio określona, elementy niediagonalne matrycy sztywności materiału są kolejno zerowane. W skrajnym przypadku pozostają tylko dodatnie składniki głównej przekątnej.

1.10. Obliczenia ugięć

Ugięcia obiektu (pręt lub powierzchni) są określane przy użyciu wcześniej obliczonej matrycy sztywności D. Wartość obliczeniowa (Design Ratio) jest obliczana z ugięcia i wartości granicznej.

1.10.1. Odpowiednie obciążenie

Jeśli odpowiednie obciążenie jest przypisane do głównego obciążenia, zostanie obliczone końcowe ugięcie jako suma pojedynczych wartości. Główna kombinacja obciążeń jest obliczana bez właściwości zależnych od czasu (pełzanie i skurcz) i powinna być zatem krótkoterminowa (częsta lub charakterystyczna). Natomiast odpowiednia kombinacja obciążeń jest zawsze obliczana z właściwościami zależnymi od czasu i powinna być zatem długoterminowa (quasi-stała). Jeśli przypisane jest więcej niż jedno odpowiednie obciążenie, obciążenie o najwyższej wartości ugięcia jest uwzględniane. Całkowite ugięcie jest obliczane w następujący sposób:

1.11 Różnice między RFEM 5 a RFEM 6

Obliczenia wysokości strefy ściskania w betonie W RFEM 5 wysokość strefy ściskania w betonie jest obliczana na podstawie netto wysokości przekroju, podczas gdy w RFEM 6 stosuje się brutto wysokość przekroju. Dzięki temu podejściu obliczenia są szybsze i bardziej przejrzyste, co również umożliwia lepsze śledzenie wyników. Ta simplifikacja utrzymuje dokładność obliczeń na wysokim poziomie, dzięki czemu wyniki w praktyce nie wykazują znaczących różnic. RFEM 6 oferuje zatem bardziej wydajne rozwiązanie przy zachowaniu precyzyjnych wyników.

Współczynnik rozkładu zbrojenia Współczynnik rozkładu opisujący rozkład naprężeń w przekroju był w RFEM 5 określany wyłącznie na podstawie naprężeń długoterminowych. Oznacza to, że brano pod uwagę jedynie naprężenia działające przez dłuższy czas. W RFEM 6 podejście obliczeniowe zostało rozwinięte tak, aby obecnie uwzględniać maksimum zarówno z naprężeń długoterminowych, jak i krótkoterminowych. Ta zmiana zapewnia bardziej realistyczne odwzorowanie rzeczywistych warunków naprężeniowych w przekroju.