Direkte Verformungsberechnung

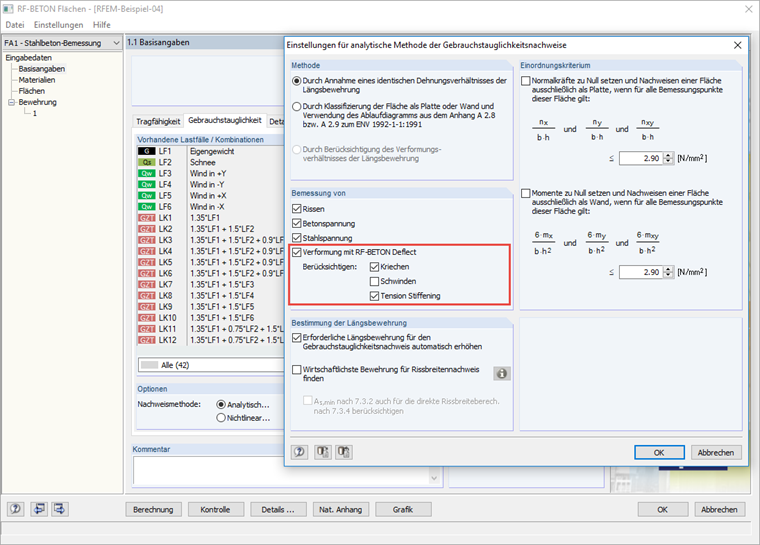
mittels Effektiver Steifigkeitsmethode (ESM)

1. Beschreibung des theoretischen Hintergrunds

Für die Verformungsanalyse im Rahmen der Betonbemessung wird ein analytisches Verfahren für 2D-Strukturen und 1D-Elemente verwendet, die Normalkräften und Biegemomenten ausgesetzt sind. Dieses basiert auf der Ermittlung effektiver Steifigkeiten (Effektive Steifigkeitsmethode) auf Querschnittsebene unter Berücksichtigung des Risszustands, sowie von Effekten wie Tension Stiffening und einfachen Langzeiteffekten (Schwinden und Kriechen).

1.1. Grundlegende Material- und Geometrieannahmen

Für die direkte Verformungsanalyse in der Betonbemessung wird ein linear-elastisches Druckverhalten sowie ein linear-elastisches Verhalten bis zur Erreichung der Zugfestigkeit angesetzt. Solche Annahmen sind für den Gebrauchstauglichkeitsnachweis ausreichend. Überschreiten die Spannungen die Betondruckfestigkeit, erfolgt die Schadensentwicklung gemäß EN 1992-1-1, Abschnitt 7.3.4.
Die Berechnung basiert auf einem einfachen isotropen Modell der Bruchmechanik, das individuell für die beiden Bewehrungsrichtungen definiert ist. Gemäß EN 1992-1-1 wird eine effektive Materialsteifigkeitsmatrix durch Interpolation zwischen dem ungerissenen Zustand (Zustand I) und dem gerissenen Zustand (Zustand II) gemäß Abschnitt 7.4.3, Gleichung (7.18), berechnet. Der Stahlbeton wird somit als orthotropes Material modelliert. Dabei werden Effekte wie Tension Stiffening sowie einfache Langzeiteffekte (Schwinden und Kriechen) berücksichtigt.
Die Berechnung der Materialsteifigkeitsmatrizen wird für die Modelltypen 2D-XY (u_z / φ_x / φ_y) und 3D umgesetzt. Beim 3D-Modell wird zusätzlich der Einfluss der Exzentrizitäten der idealen Schwerpunkte in der Steifigkeitsmatrix berücksichtigt.

1.2. Bemessungsinnere Kräfte

Wie oben beschrieben, basiert die Berechnung der Steifigkeiten auf linear - elastischen Annahmen. Die inneren Kräfte werden orthogonal zur Bewehrungsrichtung ф und auf die beiden Oberflächen s (oben und unten) transformiert. Die erhaltenen inneren Kräfte – Biegemomente m_s,ф und Normalkräfte n_s,ф (Torsionsmomente werden durch Transformation eliminiert) – hängen ab von:
(a) Modelltyp;
(b) Berechnungsverfahren;
(c) Klassifikationskriterium.

1.3. Kritische Oberfläche

Zur Bestimmung der kritischen Oberfläche wird jede Bewehrungsrichtung ф separat betrachtet. Der Spannungszustand wird auf der unteren Oberfläche (in Richtung der lokalen +z-Achse) und der oberen Oberfläche (in Richtung der lokalen -z-Achse) analysiert. Diejenige Oberfläche mit der größeren Betonzugspannung gilt als maßgebend. Die inneren Kräfte auf den kritischen Oberflächen werden als n_ф und m_ф bezeichnet.

Die Normalkraft n_ф,s, die in die Bewehrungsrichtung ф transformiert wurde, hat für beide Oberflächen denselben Wert (n_ф = n_ф,oben = n_ф,unten). Daher sind die Normalkräfte für die Bestimmung der kritischen Oberfläche nicht relevant; nur die Biegemomente werden betrachtet, um die maßgebende Oberfläche zu finden. Die Vorzeichen der Biegemomente m_ф,s werden danach bestimmt, ob die Momente Zug oder Druck auf der jeweiligen Oberfläche verursachen. Die kritische Oberfläche ist diejenige mit dem größeren Biegemoment (also die stärker auf Zug beanspruchte Oberfläche).

Für die Berechnung der Steifigkeiten werden nur die inneren Kräfte n_ф und m_ф auf der kritischen Oberfläche berücksichtigt. Bislang bezog sich der Begriff "untere Oberfläche" auf die lokale +z-Achse. Im Folgenden bezieht sich "untere Oberfläche" jedoch auf die maßgebende Seite der Oberfläche.

1.4. Querschnittseigenschaften

Die Querschnittseigenschaften werden für beide Bewehrungsrichtungen und für beide Querschnittszustände c (gerissen / ungerissen) bestimmt. Für Zustand I (ungerissener Querschnitt) wird ein linear - elastisches Verhalten des Betons bei Zug angesetzt. Für Zustand II (gerissener Querschnitt) wird die Zugfestigkeit des Betons nicht berücksichtigt.

Die Berechnung der geometrischen Parameter ist für Zustand I unabhängig von den inneren Kräften, sodass eine direkte Berechnung möglich ist. Für Zustand II wird die Tiefe der neutralen Achse iterativ berechnet. Aus numerischen Gründen verwendet das Programm den minimalen Bewehrungsgrad ρ_min = 10^-4 für beide entscheidenden Oberflächen (oben und unten), jedoch nur bei positivem Normalkraftanteil. Das bedeutet, dass bei fehlender Bewehrung eine virtuelle minimale Bewehrungsfläche angesetzt wird. Ein solch kleiner Wert hat keinen nennenswerten Einfluss auf die Ergebnisse (Steifigkeiten).

Die berechneten idealen Querschnittseigenschaften (bezogen auf den Betonquerschnitt) in einer Bewehrungsrichtung ф und für den Risszustand c sind:
(a) Trägheitsmoment zum idealen Schwerpunkt I_c,ф
(b) Trägheitsmoment zum geometrischen Schwerpunkt des Querschnitts I_0,c,ф
(c) Querschnittsfläche A_c,ф
(d) Exzentrizität des idealen Schwerpunkts e_c,ф

1.5. Langzeiteffekte

Schwinden und Kriechen sind zeitabhängige Eigenschaften von Beton. Gemäß EN 1992-1-1 sind die Langzeiteffekte separat zu berücksichtigen.

1.5.1. Kriechen

Die Kriech-Effekte werden durch eine Reduktion des Elastizitätsmoduls des Betons E_c berücksichtigt, wobei der effektive Kriechkoeffizient ϕ_eff gemäß EN 1992-1-1, Gleichung (7.20), verwendet wird:

1.5.2. Schwinden

In der Durchbiegungsberechnung gemäß EN 1992-1-1 gibt es zwei Aspekte, die durch Schwindeffekte beeinflusst werden.

1.5.2.1. Reduktion der Materialsteifigkeit
Die Materialsteifigkeit in jeder Bewehrungsrichtung φ wird durch einen sogenannten Schwindeinflusskoeffizienten k_sh,c,φ reduziert. Für beide Risszustände c (gerissen / ungerissen) werden die Schwindnormalkräfte n_sh,c,φ und Biegemomente m_sh,c,φ aus der freien Schwindverformung ε_sh bestimmt:

Abb. 1.1: Innere Kräfte n_sh,ф und m_sh,ф
Mit diesen inneren Kräften aus dem Schwinden wird die zusätzliche Krümmung κ_sh,c,ф an dem analysierten Punkt berechnet – ohne den Einfluss des umgebenden Modells. Anschließend wird der Schwindeinflusskoeffizient

Der Koeffizient k_sh,c,ф ist auf den Bereich k_sh,c,ф ∈ (1, 100) begrenzt. Somit darf k_sh,c,ф die Steifigkeit nicht um mehr als das 100-Fache reduzieren (aus numerischen und physikalischen Gründen). Der Minimalwert k_sh,c,ф = 1,0 bedeutet, dass der Einfluss der Schwindens nicht berücksichtigt werden kann, wenn diese eine entgegengesetzte Orientierung zur durch Belastung verursachten Krümmung κ_d aufweist. Wenn Schwinden deaktiviert ist, entspricht der Koeffizient k_sh,c,ф = 1,0.
Der Einfluss des Schwindens auf die Membransteifigkeit wird nicht berücksichtigt.

1.5.2.2. Berechnung des Verteilungskoeffizienten
Der zweite Einfluss des Schwindens betrifft die Berechnung des Verteilungskoeffizienten (Schadensparameter) ζ gemäß EN 1992-1-1, Abschnitt 7.4.3, Gleichung (7.18). Das folgende Kapitel beschreibt den Verteilungskoeffizienten im Detail.

1.6. Verteilungskoeffizient

Die Berechnung des Verteilungskoeffizienten ζ_d wird für die Bewehrungsrichtung ф dargestellt. Zuerst berechnet das Programm die maximale Betonzugspannung σ_max,ф unter der Annahme eines linear-elastischen Materialverhaltens. Wenn Langzeiteffekte (Kriechen oder Schwinden) aktiviert sind, muss die maximale Spannung zweimal berechnet werden, andernfalls nur einmal.

Kurzzeitberechnung: Prüft, ob Risse unmittelbar nach der Belastung auftreten.
Langzeitberechnung: Berücksichtigt das Rissverhalten mit Einfluss von Kriechen oder Schwinden am Ende des betrachteten Zeitraums.

Berechnungsschritte:
Bei aktiviertem Kriechen: Kurzzeitgeometrische Parameter und maximale Spannung werden berechnet.
Bei aktiviertem Schwinden: Es ist nur notwendig, die Kurzzeitspannung neu zu berechnen. Danach wird die finale maximale Spannung σ_max,ф als Maximum aus der Langzeitspannung σ_max,lt,ф und der Kurzzeitspannung σ_max,st,ф berechnet.

Der Einfluss der Schwindkraft auf die maximale Zugspannung σ_max,ф wird durch die zusätzlichen inneren Kräfte aus Schwinden berücksichtigt. Die Berechnung des Verteilungskoeffizienten ζ_d,ф hängt davon ab, ob das Tension-Stiffening gemäß EN 1992-1-1 bei der Verformungsberechnung berücksichtigt wird.

1.6.1. Verteilungskoeffizient ζ_d,ф unter Berücksichtigung von Tension-Stiffening

1.6.2. Verteilungskoeffizient ζ_d,ф ohne Berücksichtigung von Tension-Stiffening

1.6.3. Erkennung des Risszustands

Die Erkennung des Risszustands kann in der Gebrauchstauglichkeitskonfiguration (Serviceability Configuration) eingestellt werden. Folgende Optionen stehen zur Verfügung:
(a) Risszustand wird basierend auf der zugehörigen Last berechnet;
(b) Risszustand basierend auf der zugehörigen charakteristischen Kombination (CO) der SLS - Bemessungssituation;
(c) Risszustand als Hüllkurve aus allen SLS-Bemessungssituationen bestimmt;
(d) Risszustand unabhängig von der Last.

Abb. 1.2: Gebrauchstauglichkeitskonfiguration
Wenn die Option Risszustand wird basierend auf der zugehörigen Last berechnet ausgewählt wird, wird der Risszustand (Verteilungskoeffizient ζ_d) nur basierend auf der aktuellen Belastung (Lastkombination) berechnet.
Wenn die Option Risszustand basierend auf der zugehörigen charakteristischen Kombination (CO) der SLS - Bemessungssituation ausgewählt wird, wird der Verteilungskoeffizient ζ_d als Maximum aus allen zugehörigen Lasten berechnet. Die zugehörigen Lasten können in der Definition der Lastkombination festgelegt werden.

Abb. 1.3: Zugehörige Lasten
Wenn die Option Risszustand als Hüllkurve aus allen SLS-Bemessungssituationen bestimmt ausgewählt wird, wird der Verteilungskoeffizient ζ_d als Maximum aus allen Bemessungssituationen berechnet. Wenn die Option Risszustand unabhängig von der Last ausgewählt wird, beträgt der Verteilungskoeffizient stets 1,0.

1.6.4. Bemessungssituationen

Im Allgemeinen wird die Durchbiegung für quasi - ständige Lasten berechnet. Es ist jedoch möglich, gewünschte Bemessungssituationen auszuwählen (in der Gebrauchstauglichkeitskonfiguration, Option Benutzerdefinierte Zuweisung des Bemessungssituationstyps), für die die Durchbiegung berechnet werden soll.
Es können folgende Gebrauchstauglichkeits-Bemessungssituationstypen ausgewählt werden:
- Quasi - ständig,
- Häufig,
- Charakteristisch.
Für jeden Typ kann ein Grenzwert für die Durchbiegung festgelegt werden (siehe Abb. 1.2). Darüber hinaus werden die gewünschten Bemessungssituationen auch für die Betonbemessung festgelegt.

Abb. 1.4: Einstellung der Bemessungssituationen für die Betonbemessung
Für die Erkennung des Risszustands (insbesondere bei der Auswahl, ob die Erkennung aus zugehörigen Lasten oder aus allen Gebrauchstauglichkeits - Bemessungssituationen erfolgt) ist die Einstellung in der Betonbemessung entscheidend.
Mit anderen Worten:
- Wenn eine Bemessungssituation in der Gebrauchstauglichkeitskonfiguration deaktiviert, aber in der Einstellung der Betonbemessung aktiviert ist, wird diese Bemessungssituation berücksichtigt.
- Wenn eine Bemessungssituation in der Gebrauchstauglichkeitskonfiguration aktiviert, aber in der Einstellung der Betonbemessung deaktiviert ist, wird diese Bemessungssituation nicht berücksichtigt.

1.7. Querschnittseigenschaften für die Verformungsanalyse

In der Materialsteifigkeitsmatrix D für die Verformungsanalyse benötigt das Programm die Querschnittseigenschaften in jeder Bewehrungsrichtung, abhängig vom Risszustand. Diese sind:
(a) Trägheitsmoment zum idealen Schwerpunkt I_ф;
(b) Trägheitsmoment zum geometrischen Schwerpunkt des Querschnitts I_0,c;
(c) Ideale Querschnittsfläche A_ф;
(d) Exzentrizität des idealen Schwerpunkts e_ф zum geometrischen Schwerpunkt.
Eine mittlere Dehnung ε_ф und eine mittlere Krümmung κ_ф werden durch Interpolation zwischen gerissenem und ungerissenem Zustand gemäß EN 1992-1-1, Gleichung (7.18), berechnet:

Die Verformung in ungerissenem und gerissenem Zustand c (Zustand I und II) wird nach den folgenden Gleichungen berechnet:

Die idealen Querschnittseigenschaften werden zum idealen Schwerpunkt des Querschnitts berechnet. Der Einfluss des Schwindens wird durch den Faktor k_sh,c,ф berücksichtigt:

Wenn die Normalkraft ungleich null ist, werden die Querschnittseigenschaften zum geometrischen Schwerpunkt des Querschnitts unter Berücksichtigung der Exzentrizität berechnet:

1.8. Materialsteifigkeitsmatrix D (Stäbe)

Die axiale Steifigkeit EA und die Biegesteifigkeit EI_y,0 werden nur in Bewehrungsrichtung ф = 1 (Richtung des Stabes) wie folgt berechnet:

1.9. Materialsteifigkeitsmatrix D (Flächen)

Bei der Berechnung der Querschnittseigenschaften wird der Anfangswert des Poisson - Verhältnisses ν_init in beiden Richtungen unabhängig voneinander gemäß folgender Gleichung reduziert:

Die Materialsteifigkeitsmatrix wird gemäß der Theorie für orthotrope Flächen berechnet.

1.9.1. Biegesteifigkeit - Platten und Schalen

Die Biegesteifigkeiten in den Bewehrungsrichtungen ф werden wie folgt bestimmt:
Für Schalen:

Für Platten:
Die nicht - diagonale Komponente der Materialsteifigkeitsmatrix ist für Platten und Schalen identisch:
Für Schalen werden die Unterschiede in den Biegesteifigkeiten aufgrund der Trägheitsmomente durch die Exzentrizitätskomponenten in der Materialsteifigkeitsmatrix ausgeglichen.

1.9.2. Torsionssteifigkeit von Platten und Schalen

Die Elemente der Steifigkeitsmatrix werden für Platten und Schalen wie folgt berechnet:

1.9.3. Schubsteifigkeit von Platten und Schalen

Die Elemente der Steifigkeitsmatrix für Schub werden bei der Verformungsanalyse nicht reduziert. Sie werden aus dem Schubmodul G des idealen Querschnitts und der Querschnittshöhe h bestimmt. Der Ausdruck ist für Schalen und Platten identisch:

1.9.4. Membransteifigkeit von Schalen

Die Membransteifigkeiten in den Bewehrungsrichtungen ф werden wie folgt berechnet:

Der nicht - diagonale Teil der Materialsteifigkeitsmatrix wird bestimmt durch:

Der Anteil der Schubsteifigkeitskomponente lautet:

1.9.5. Exzentrizität – Schalen

Die Elemente der Steifigkeitsmatrix für die Exzentrizität des Schwerpunkts (idealer Querschnitt) in der Bewehrungsrichtung ф werden wie folgt berechnet:

Der nicht - diagonale Teil der Materialsteifigkeitsmatrix wird bestimmt durch:

Die Exzentrizitätskomponente für Torsion wird wie folgt berechnet:

1.9.6. Test auf positive Definitheit

Die positive Definitheit der Materialsteifigkeitsmatrix D wird mittels eines modifizierten (unter Berücksichtigung der Nullblöcke) SYLVESTER‘S - Kriteriums getestet.
Falls die Steifigkeitsmatrix D nicht positiv definit ist, werden die nicht - diagonalen Komponenten der Materialsteifigkeitsmatrix sukzessive auf null gesetzt. Im Extremfall bleiben nur die positiven Komponenten der Hauptdiagonale erhalten.

1.10. Berechnung von Durchbiegungen

Die Durchbiegungen eines Objekts (Stab oder Fläche) werden mithilfe der vorab berechneten Steifigkeitsmatrix D ermittelt. Der Bemessungswert (Design Ratio) wird aus der Durchbiegung und dem Grenzwert berechnet.

1.10.1. Zugehörige Last

Wenn eine zugehörige Last der Hauptlast zugewiesen wird, wird die endgültige Durchbiegung als Summe der einzelnen Werte berechnet. Die Hauptlastkombination wird ohne zeitabhängige Eigenschaften (Kriechen und Schwinden) berechnet und sollte daher kurzfristig sein (häufig oder charakteristisch). Die zugehörige Lastkombination wird hingegen immer mit zeitabhängigen Eigenschaften berechnet und sollte daher langfristig sein (quasi - ständig). Wenn mehr als eine zugehörige Last zugewiesen wird, wird diejenige mit dem höchsten Wert der Durchbiegung berücksichtigt.
Die Gesamtdurchbiegung wird wie folgt berechnet:

1.11 Unterschiede zwischen RFEM 5 und RFEM 6

Berechnung der Höhe der Betondruckzone
In RFEM 5 wird die Höhe der Betondruckzone auf Basis der netto Querschnittshöhe berechnet, während in RFEM 6 die brutto Querschnittshöhe verwendet wird. Diese Vorgehensweise sorgt für eine schnellere und übersichtlichere Berechnung, die auch eine bessere Nachvollziehbarkeit der Ergebnisse ermöglicht. Durch diese Vereinfachung bleibt die Genauigkeit der Berechnung auf hohem Niveau, sodass die Ergebnisse in der Praxis keine signifikanten Unterschiede aufweisen. RFEM 6 bietet somit eine effizientere Lösung bei gleichbleibend präzisen Resultaten.

Verteilungsbeiwert der Bewehrung
Der Verteilungsbeiwert, der die Spannungsverteilung über den Querschnitt beschreibt, wurde in RFEM 5 ausschließlich auf der Grundlage der langzeitwirkenden Spannung bestimmt. Dies bedeutet, dass nur die Spannung berücksichtigt wurde, die über einen längeren Zeitraum hinweg wirkt. In RFEM 6 wurde der Berechnungsansatz weiterentwickelt, sodass jetzt das Maximum aus sowohl der Langzeit- als auch der Kurzzeitspannung berücksichtigt wird. Diese Änderung sorgt für eine realistischere Abbildung der tatsächlichen Spannungsverhältnisse im Querschnitt.