The state of an enclosed gas can be described by the presumptions of the thermodynamic equilibrium. This results in the following general gas equation:
p ∙ V = n ∙ R ∙ T
with the state variables where
p is the pressure,
V is the volume,
n is the is the amount of substance,
R is the universal gas constant,
T is the temperature.
Ideal Gas Properties
When keeping certain state variables constant in the general gas equation, special properties of the ideal gas arise. It is useful to know these properties for using ideal gases in the structural analysis, and it helps to simulate certain load conditions accordingly.
Isothermal Change of State (Boyle-Mariotte)
If variables T and n are constant and acting pressure p is increased, volume V of the considered gas unit is reduced.
The following applies:
Isobaric Process (Gay-Lussac)
If variables p and n are constant and acting temperature T is increased, volume V of the considered gas unit increases.
The following applies:
Isochoric Process (Amotons)
If variables V and n are constant and acting temperature T is increased, pressure p of the considered gas unit increases.
The following applies:
Application in Structural Analysis
In structural analysis, encased gases are usually used to transfer the external forces. In this case, it is required that the force acting locally on a certain location on the volume casing is transported by the enclosed gas to all other sides of the volume casing.
This property is used, for example, in insulated glass panes or inflated membrane cushions. In both cases, the volume casing is described by the load-bearing elements and filled with a gas. The volume limitations consist of rigid shell elements in the case of insulated glass panes, and flexible membrane elements in the case of membrane cushions. However, to use one example, wind or snow load acts on one side of the volume limitation in both cases, and is transferred by the enclosed gas to the adjacent volume limitations.
Since the temperature does not change suddenly in the load situations considered in structural analysis, the ideal gas with isothermal properties is usually simulated in the volume casing.
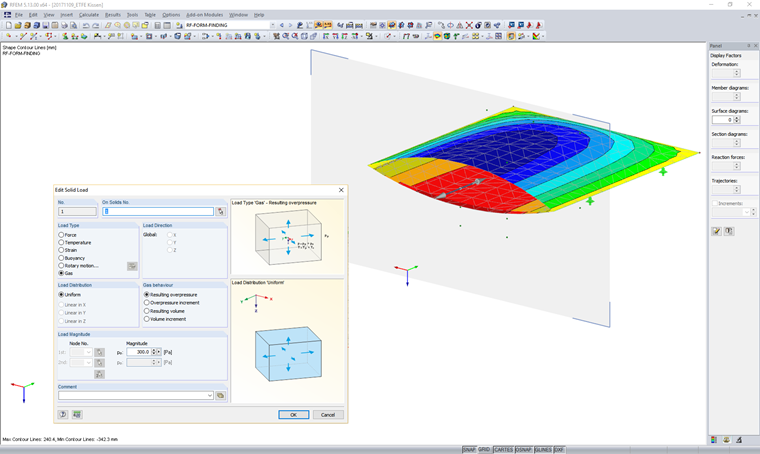
Implementation in RFEM
Solids can be defined in RFEM. These solids are described by the surrounding surfaces. In this type of volume cell of the surrounding shell and solid components, the solid definition can be inscribed with the gas type. This resulting gas volume requires describing the enclosed gas and determining the atmospheric state variables. The atmospheric state variables have no impact on the enclosed volume and only describe the initial situation for the simulation.
In the assigned load cases, the corresponding solid load can be applied for each gas solid. To simulate open or closed solids, it is possible to specify the resulting pressures/volumes or the pressure/volume changes.