Shear Resistance According to ACI 318-19 in RFEM 6

Introduction

In the previous standard ACI 318-14 [2], eight equations are specified for the calculation of the shear strength V_c - without considering the application limits. The user can choose between a simplified and an exact calculation method. One of the objectives of the new concept in ACI 318-19 was to reduce the design equations for V_c. Furthermore, the concept should consider the influence of the component height, the longitudinal reinforcement ratio, and the normal stress.

Shear Resistance V_c According to ACI 318-19

For non-prestressed reinforced concrete beams, the shear resistance V_c is calculated according to ACI 318-19 [1] with Equations a) to c) from Table 22.5.5.1. With the new Equations b) and c), the member height, the longitudinal reinforcement ratio, and the normal stress now influence the shear strength, V_c. Equation a) was basically taken from ACI 318-14 [2]. The determination of the shear resistance V_c according to Table 22.5.5.1 [1], depends on the inserted shear reinforcement A_v. If the minimum shear reinforcement A_v,min according to 9.6.3.4 is available or exceeded, the calculation of V_c may be performed either according to Equation a) or Equation b) from Table 22.5.5.1 [1]. 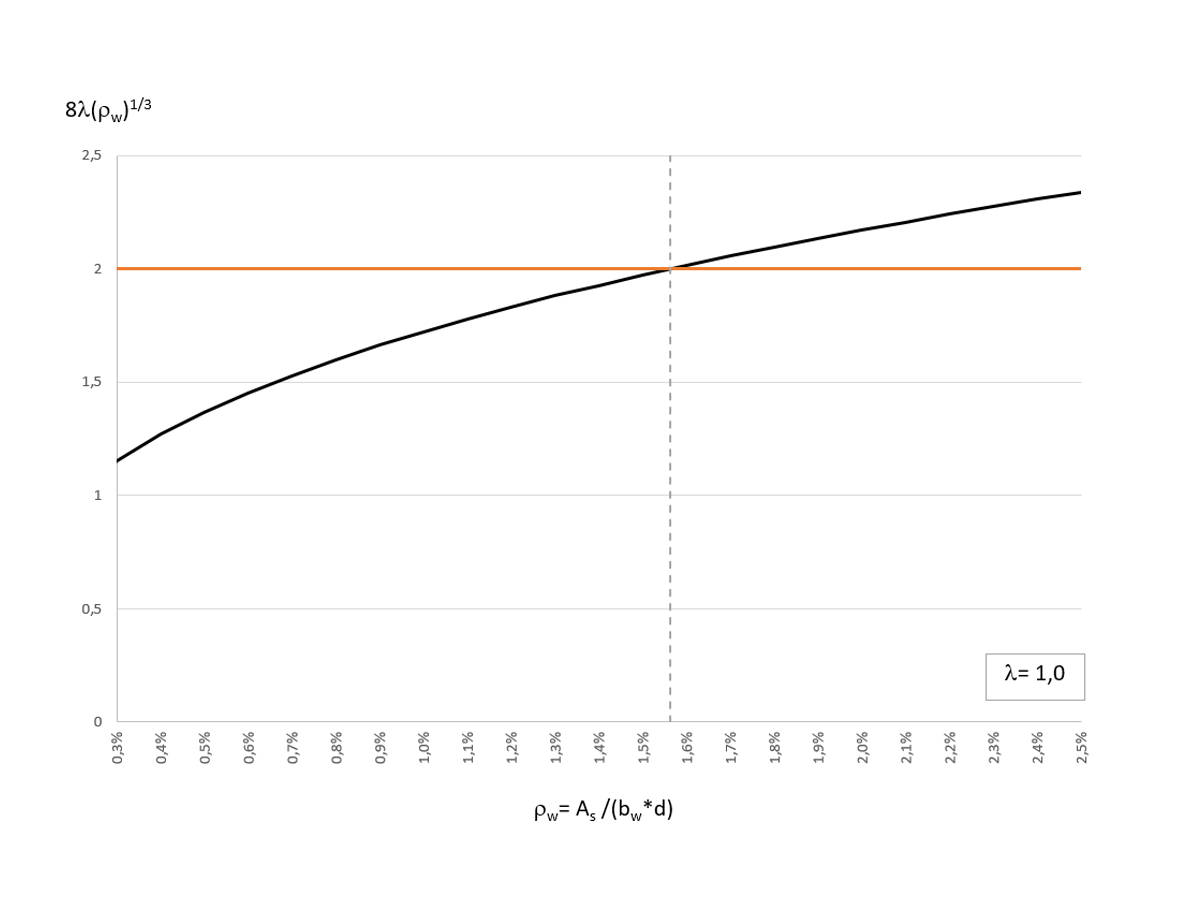If you compare the two equations shown above, you can see that in Equation b), the factor 2 λ has been replaced by the term 8 λ (ρ_w)1/3. The longitudinal reinforcement ratio ρ_w influences the calculation of the shear resistance V_c. Figure 01 shows the distribution of 8 λ (ρ_w)1/3 as a function of ρ_w (with λ = 1).

For λ = 1.0, 8 λ (ρ_w)^1/3 becomes equal to the value 2 λ for a longitudinal reinforcement ratio ρ_w = 1.56%. When calculating V_c, Equation a) for λ= 1 and a longitudinal reinforcement ratio ρ_w (greater than) 1.56% and Equation b) for λ= 1 and ρ_w > 1.56% results in the greater concrete shear resistance. The standard allows the application of both equations. Therefore, the maximum value from Equations a) and b) can be used for a cost-effective design. For beams with shear reinforcement A_v less than A_v,min, Equation c) of Table 22.5.5.1 [1] is to be used according to ACI 318-19 [1]. 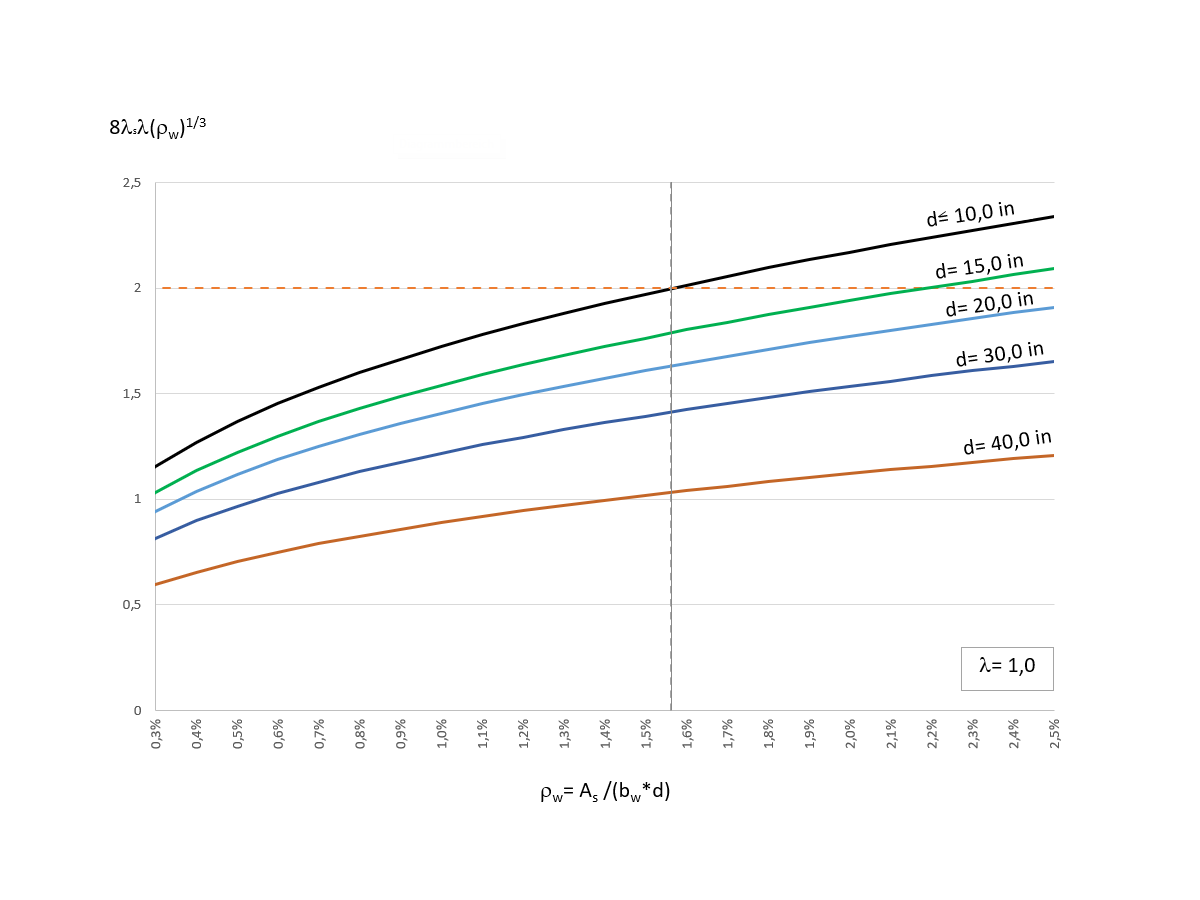Except for variable λ_s, Equation c) is similar to Equation b) discussed above. For structural components with little or no shear reinforcement, the concrete shear resistance V_c decreases with increasing structural component height. By introducing the factor λ_s, the "Size Effect" is taken into account. The factor λ_s is determined according to Equation 22.5.5.1.3 [1] as follows. The reduction of the shear resistance V_c,c by the factor λ_s is only effective for structural heights d (greater than) 10in. Figure 02 shows the distribution of term 8 λ_s λ (ρ_w)^1/3 for the different effective depths d.

Example: Calculate Required Shear Reinforcement According to ACI 318-19

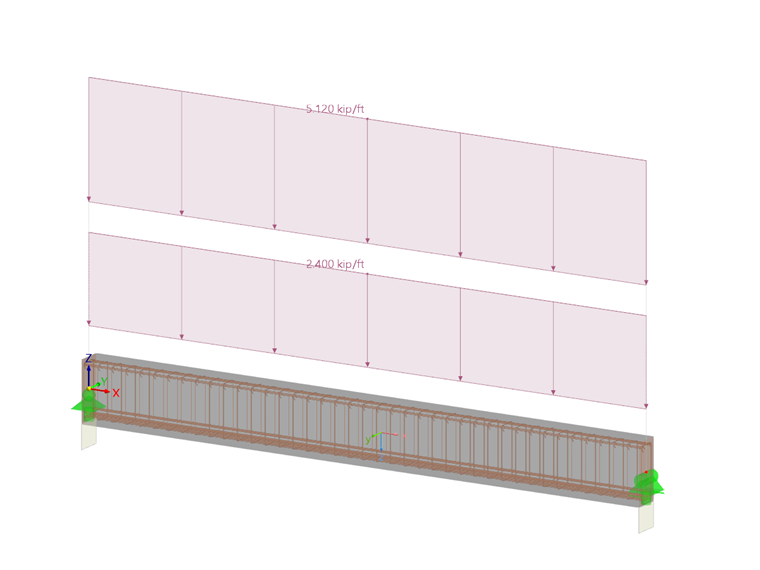
The following section describes how to determine the required shear reinforcement according to the new concept of ACI 318-19 [1] for a reinforced concrete beam, which was designed in a previous Knowledge Base Article according to ACI 318-14 [2]. Figure 03 shows the structural model and the design load.

The rectangular cross-section has the dimensions 25 in. · 11 in. The concrete has a compressive strength of f'_c = 5,000 psi. The yield strength of the reinforcing steel used is f_y = 60,000 psi. The effective depth of the tension reinforcement is applied with d = 22.5 in. The design value of the acting shear force V_u at a distance d from the support is 61.10 kips. The determination of the shear resistance V_s according to Table 22.5.5.1 [1] depends on the height of the inserted shear reinforcement A_v. The prerequisite for using Equations a) and b) is that the minimum shear reinforcement according to 9.6.3.4 [1] is applied. For this reason, a check is performed in the first step as to whether a minimum reinforcement has to be considered according to 9.6.3.1 [1].

61.10 kips > 13.13 kips

This requires a minimum shear reinforcement. This is calculated according to 9.6.3.4 [1], as follows. a_v,min = 0.12 in²/ft

When considering the minimum shear reinforcement, the concrete shear resistance V_c can now be determined with Equations a) or b) of Table 22.5.5.1 [1]. The shear resistance V_c,a according to Equation a) is calculated as V_c,a = 35.0 kips. To apply Equation b), it is necessary to know the longitudinal reinforcement ratio ρ_w. To be able to compare the calculated shear reinforcement with the calculation result of the Concrete Design Add-on, ρw is determined with the required longitudinal reinforcement at the distance d from the support. A bending moment of M_y,u = 1533 kip-in results in a longitudinal reinforcement of A_s,req = 1.33 in², which is ρ_w = 0.536%. Figure 01 shows the influence of the longitudinal reinforcement ratio ρw on the calculation of V_c,b. Since ρ_w (less than) 1.5% here, Equation b) will result in a lower shear resistance V_c,b than Equation a) and we can skip determining V_c,b. However, we calculate V_c,b to show it.

V_c,b = 24.52 kips

As expected, Equation b) provides a lower shear resistance than Equation a). Additionally, the shear resistance V_c is limited to the maximum value V_c,max according to 22.5.5.1.1 [1]. a_v,min = 0.12 in²/ft

When considering the minimum shear reinforcement, the concrete shear resistance V_c can now be determined with Equations a) or b) of Table 22.5.5.1 [1].

Maximum Value of Shear Resistance of Concrete Vc, max According to ACI 318-19, 22.5.5.1.1

The shear resistance V_c,a according to Equation a) is calculated as V_c,a = 35.0 kips.

To apply Equation b), it is necessary to know the longitudinal reinforcement ratio ρ_w. To be able to compare the calculated shear reinforcement with the calculation result of the Concrete Design Add-on, ρ_w is determined with the required longitudinal reinforcement at the distance d from the support. A bending moment of M_y,u = 1533 kip-in results in a longitudinal reinforcement of A_s,req = 1.33 in², which is ρ_w = 0.536%. Figure 01 shows the influence of the longitudinal reinforcement ratio ρ_w on the calculation of V_c,b. Since ρ_w (greater than) 1.5% here, Equation b) will result in a lower shear resistance V_c,b than Equation a) and we can skip determining V_c,b. However, we calculate V_c,b to show it.

V_c,b = 24.52 kips

As expected, Equation b) provides a lower shear resistance than Equation a). Additionally, the shear resistance V_c is limited to the maximum value V_c,max according to 22.5.5.1.1 [1].

Maximum Value of Shear Resistance of Concrete Vc, max According to ACI 318-19, 22.5.5.1.1

V_c,max = 87.5 kips

Finally, the calculation of the required shear reinforcement results in the following applicable concrete shear force resistance V_c.

V_c = max [V_c,a; V_c,b ] ≤ V_c,max

V_c = [35.0 kips; 24.5 kips] ≤ 87.5 kips

V_c = 35.0 kips

The required shear reinforcement req. a_v is calculated as follows: Req. a_v = 0.41 in²/ft ≥ 0.12 in²/ft

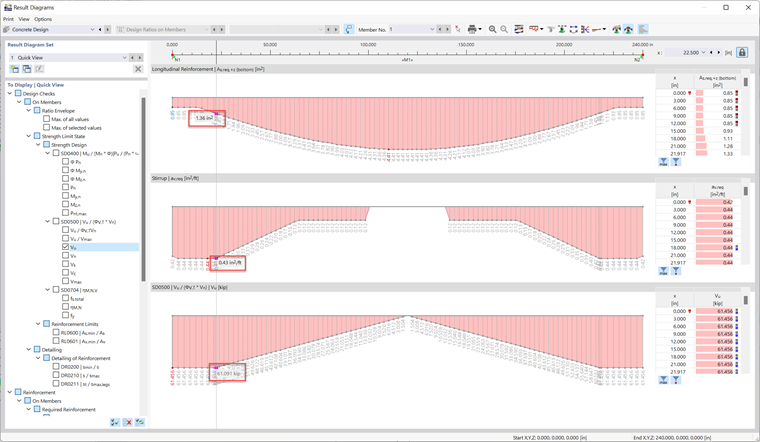
The reinforced concrete design according to ACI 318-19 [1] can be performed with RFEM 6. The Concrete Design Add-on also calculates a required shear reinforcement of 0.43 in²/ft at the distance d from the support (see Figure 04).

Note: The results in RFEM 6 differ from the hand calculations slightly due to a more accurate value for the Depth (d) calculated. RFEM 6 takes into account that there are multiple layers of tension reinforcement where the hand calculations assume a single layer.

Finally, the maximum load capacity of the concrete compression strut of the shear truss is verified according to Section 22.5.1.2. 61.10 kips ≤ 175.00 kips.

The shear design according to ACI 318-19 is fulfilled. As expected, Equation b) provides a lower shear resistance than Equation a).

Additionally, the shear resistance V_c is limited to the maximum value V_c,max according to 22.5.5.1.1 [1].

Summary

ACI 318-19 [1] introduced a new concept to determine the shear resistance V_c. It was possible to reduce the number of potential design equations from the previous version to three equations while taking into account the influence of the normal stress, the component height, and the longitudinal reinforcement ratio. This simplifies the calculation of the shear resistance V_c.