Manuali online RFEM 6 / RSTAB 9 | Verifica calcestruzzo

Torna a Manuali online

915x

005923

Dipl.-Ing. Juliane Stopper-Akdag

2025-01-21

Seleziona il manuale

Panoramica

Add-on Verifica calcestruzzo

Basi teoriche

Parametri di analisi

Specifiche di progetto

progettazione

Risultati

Tabelle per Verifica calcestruzzo
Grafico per la progettazione del calcestruzzo
- Verifiche di progetto
  
  aste
  
  Rappresentanti aste
  
  Superfici
  
  nodi
- Armatura
  
  aste
  
  Rappresentanti aste
  
  Superfici
  
  nodi
Output dettagliato dei risultati

Documentazione

Considerazione della viscosità

Considerazione del ritiro

Il ritiro descrive la deformazione del calcestruzzo sotto carico nel tempo. Le principali influenze sono simili a quelle del ritiro igrometrico. Inoltre, la cosiddetta "tensione che causa ritiro" ha un'influenza significativa sulle deformazioni da ritiro.

Per il ritiro, si devono considerare la durata del carico, il momento dell'applicazione del carico e l'entità dello sforzo. Il ritiro è rappresentato dal coefficiente di ritiro φ(t,t₀) al tempo t.

L'attivazione del ritiro avviene nella finestra di dialogo del materiale nella sezione Valori di riferimento dipendenti dal tempo del calcestruzzo. Lì vengono determinati l'età del calcestruzzo al momento considerato e all'inizio del carico, l'umidità relativa e il tipo di cemento. Il programma calcola quindi il coefficiente di ritiro φ.

Calcolo del coefficiente di ritiro

Il calcolo del coefficiente di ritiro φ è brevemente presentato secondo EN 1992-1-1, sezione 3.1.4. Prerequisito per le equazioni descritte successivamente è che la tensione che provoca ritiro σ_c del carico permanente in atto non superi il valore seguente.

σ_c ≤ 0,45 · f_ckj con f_ckj - resistenza a compressione cilindrica del calcestruzzo al momento dell'applicazione della tensione che provoca ritiro

Diagramma delle tensioni σc e delle deformazioni del materiale nel tempo

Tensione di scorrimento σc

Assumendo un comportamento lineare del ritiro (σ_c << 0,45 ⋅ f_ckj), il ritiro del calcestruzzo può essere stimato riducendo il modulo di elasticità del calcestruzzo.

E_{c, eff} = \frac{E_{cm}}{1.0 + φ (t, t_{0})}

E_cm	Modulo di elasticità medio secondo EN 1992-1-1, Tabella 3.1
φ(t,t₀)	Coefficiente di viscosità
t	Età del calcestruzzo nel momento rilevante in giorni
t₀	Età del calcestruzzo quando inizia l'applicazione del carico in giorni

Viscosità del calcestruzzo

Secondo EN 1992-1-1, sezione 3.1.4, il coefficiente di ritiro φ(t,t₀) al tempo t considerato può essere calcolato come segue.

ϕ (t, t_{0}) = ϕ_{RH} \cdot β (f_{cm}) \cdot β (t_{0}) \cdot β (t, t_{0})

β(f_cm)	coefficiente per considerare la resistenza a compressione del calcestruzzo
β(t₀)	coefficiente per considerare l'età del calcestruzzo

Il coefficiente di viscosità φ(t,t₀ ) nel punto di tempo analizzato t

β (f_{cm}) = \frac{16 . 8}{\sqrt{f_{cm}}}

Coefficiente per considerare la resistenza a compressione del calcestruzzo

β (t_{0}) = \frac{1}{0.1 + {t_{0 . eff}}^{0.2}}

coefficiente per considerare l'età del calcestruzzo

φ_{RH} = 1 + \frac{1 - \frac{RH}{100}}{0.10 \cdot \sqrt[3]{h_{0}}} \cdot α_{1} \cdot α_{2}

h₀	Spessore efficace del componente strutturale [mm] (per superfici: h₀ = h)
α₁	coefficiente di adattamento
α₂	Anpassungsfaktor

Formula_φUR

h_{0} = \frac{2 \cdot A_{c}}{u}

A_c	area della sezione trasversale
u	Perimetro della sezione trasversale

Spessore efficace del componente strutturale [mm] (per superfici: h₀ = h)

α_{1} = {(\frac{35}{f_{cm}})}^{0.7}

f_cm	Resistenza a compressione cilindrica media

Coefficiente di correzione α₁

α_{2} = {(\frac{35}{f_{cm}})}^{0.2}

f_cm	Resistenza a compressione cilindrica media

Coefficiente di correzione α₂

t_{0 . eff} = t_{0} {[1 + \frac{9}{2 + {t_{0}}^{1.2}}]}^{α} \geq 0.5 \cdot d

Formel t_0.eff

β (t, t_{0}) = {[\frac{t - t_{0}}{β_{H} + t - t_{0}}]}^{0.3}

t	Età del calcestruzzo nel momento rilevante in giorni
t₀	Betonalter zu Belastungsbeginn in Tagen

Coefficiente per tener conto della durata del carico

β_{H} = 1.5 \cdot {[1 + {(0.012 \cdot RH)}^{18}]}^{α} \cdot h_{0} + 250 \cdot α_{3} \leq 1500 \cdot α_{3}

RH	umidità relativa [%]
h₀	spessore efficace del componente [mm]
α₃	coefficiente di adattamento

Formula β_H

α_{3} = {(\frac{35}{f_{cm}})}^{0.5}

f_cm	Valore medio della resistenza a compressione del cilindro

Coefficiente di correzione α_3°

L'influenza del tipo di cemento sul coefficiente di ritiro del calcestruzzo può essere considerata modificando l'età del carico t₀ usando la seguente equazione.

t_{0} = t_{0, T} \cdot {(1 + \frac{9}{2 + {(t_{0, T})}^{1.2}})}^{α} \geq 0.5

t₀, t_T

età efficace del calcestruzzo quando inizia l'applicazione del carico, tenendo conto dell'influenza della temperatura

esponente a seconda del tipo di cemento:

-1 : cementi a indurimento lento (S) (32,5)
0 : cementi a indurimento normale o rapido (N) (32.5 R; 42.5)
1 : cementi ad alta resistenza a rapido indurimento (R) (42.5 R; 52.5)

Età del carico t₀

Considerazione computazionale del ritiro

Se le deformazioni sono note al tempo t = 0 e a un tempo successivo t, il coefficiente di ritiro φ può essere determinato per la considerazione computazionale nel modello.

φ_{t} = \frac{ε_{t}}{ε_{t = 0}} - 1

Coefficiente di viscosità

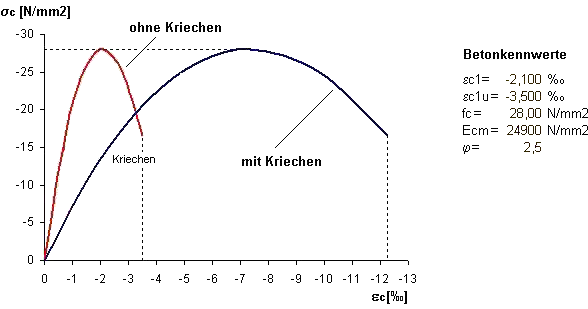
Questa equazione è riorganizzata per la deformazione al tempo t. Il seguente rapporto è valido per tensioni costanti:

ε_{t} = ε_{t = 0} \cdot (φ_{t} + 1)

relazione che è valida per tensioni uniformi

Per tensioni maggiori di circa 0,4 ⋅ f_ck, le deformazioni aumentano in modo sproporzionato, perdendo così il riferimento assunto linearmente.

Il calcolo utilizza la soluzione utile per scopi pratici in edilizia consentita secondo EN 1992-1-1, 5.8.6 (3). La curva tensione-deformazione del calcestruzzo è distorta del fattore (1 + φ).

Linea tensione-deformazione nel cemento armato per rilevare l'effetto del creep

Deformazione della curva tensione-deformazione nel calcestruzzo armato

Come visibile nella precedente immagine, la considerazione del ritiro riguarda il caso di tensioni costanti che provocano ritiro durante il periodo di carico. Questa assunzione porta a una leggera sovrastima della deformazione a causa di non considerati trasferimenti di tensione. La riduzione della tensione senza variazione della deformazione (rilassamento) è catturata in questo modello solo parzialmente. Presupponendo un comportamento elastico lineare, si potrebbe ipotizzare una proporzionalità e la distorsione orizzontale rifletterebbe il rilassamento in rapporto (1 + φ). Tuttavia, questa relazione va persa nella relazione non lineare tra tensione e deformazione.

Questo chiarisce che questo approccio deve essere inteso come un'approssimazione. Una riduzione delle tensioni a causa del rilassamento e il ritiro non lineare non possono quindi essere rappresentati o possono essere rappresentati solo approssimativamente.

Capitolo principale

Comportamento dipendente dal tempo - Viscosità e ritiro