Equation According to Pasternak
where
H is the foundation thickness,
μ is the Poisson's ratio.
Equation According to Barwaschow
where
H is the foundation thickness,
μ is the Poisson's ratio.
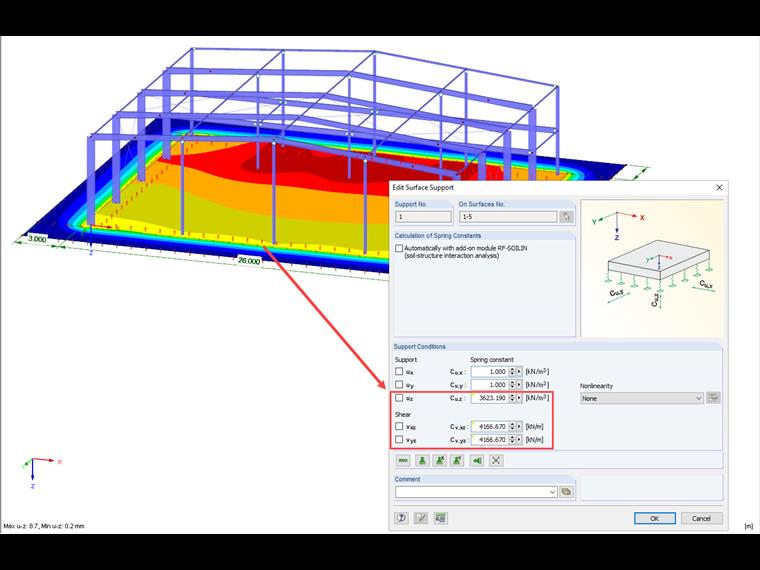
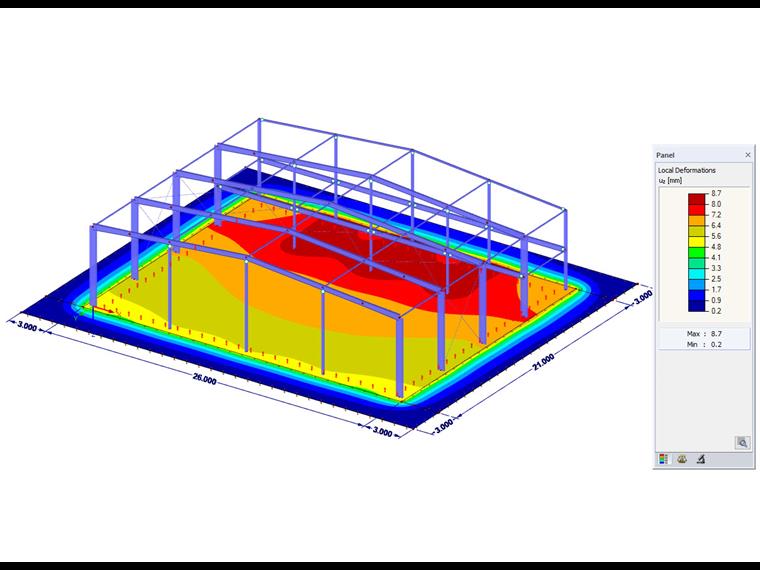
The foundation overlaps applied to this method should ideally reach until the settlement on the edge of the foundation overlap is close to zero. Moreover, the additional area should not have any additional governing stiffness, which is why the foundation overlap thickness should be kept very low.
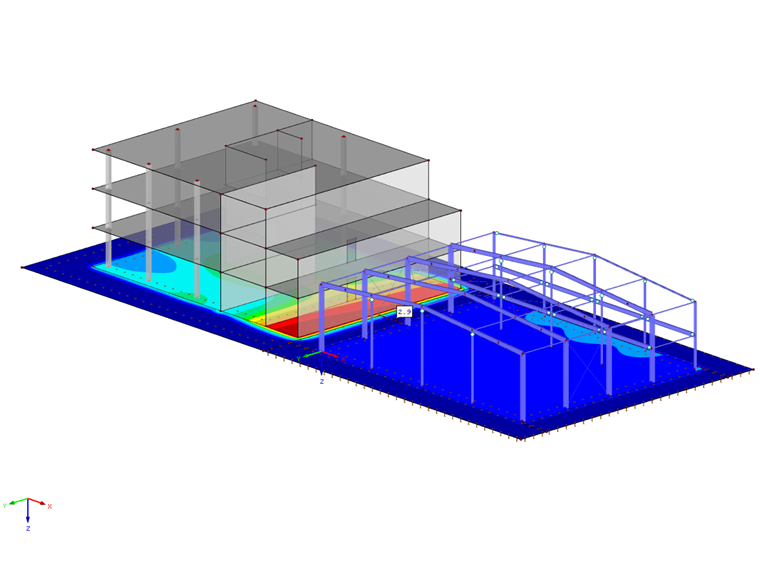
In addition to the short calculation time, an advantage of this variant is the consideration of the shear resistance. Furthermore, this method allows you to graphically display the settlement behavior outside of the foundation edge. This way, it is also possible to represent the interaction between several separate buildings that have an influence on each other via the subsidence basin.
Example
E0 = 10,000 kN/m²
μ = 0.2
H = 3 m
References
[1] Barth, C., & Rustler, W. (2013). Finite Elemente in der Baustatik-Praxis, (2nd ed.). Berlin, Beuth. [2] Kolar, V., & Nemec, I. (1989). Modelling of Soil-Structure Interaction. Amsterdam, Elsevier Science Publishers.