Przepływ stacjonarny

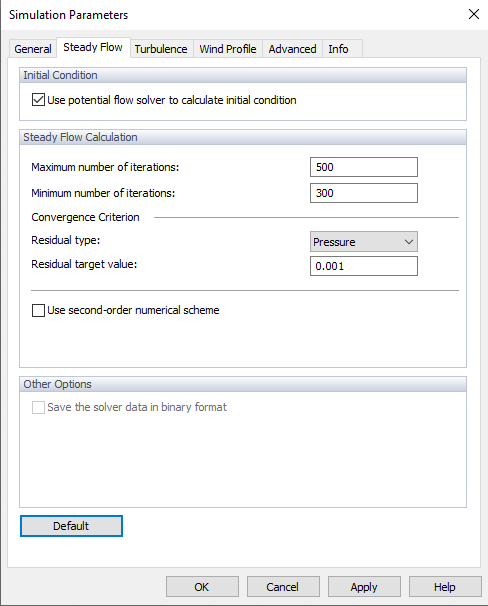
Obliczenia przepływu stacjonarnego można wybrać w zakładce „Ogólne” w oknie dialogowym „Parametry symulacji” (patrz obrazek Parametry symulacji ).

Parametry symulacji, stały przepływ

Warunki początkowe

Po aktywowaniu opcji "Wykorzystać przepływ potencjalny do obliczenia warunku początkowego" do wygenerowania warunków początkowych wykorzystywana jest zlinearyzowana wersja nielepkich równań Naviera‑Stokesa.

Obliczenia przepływu stacjonarnego

Można zdefiniować "Maksymalną liczbę iteracji". Domyślnie ograniczenie to wynosi 500 iteracji. Jeżeli obliczenia są zbieżne w mniejszej liczbie iteracji, są zatrzymywane. Można również zdefiniować "Minimalną liczbę iteracji", która jest domyślnie ustawiona na 300 iteracji (patrz ilustracja Opcje programu ), niezależnie od tego, czy kryterium zbieżności (patrz niżej) zostało już spełnione. Maksymalna liczba jest przydatna, aby uniknąć nieskończonych pętli.

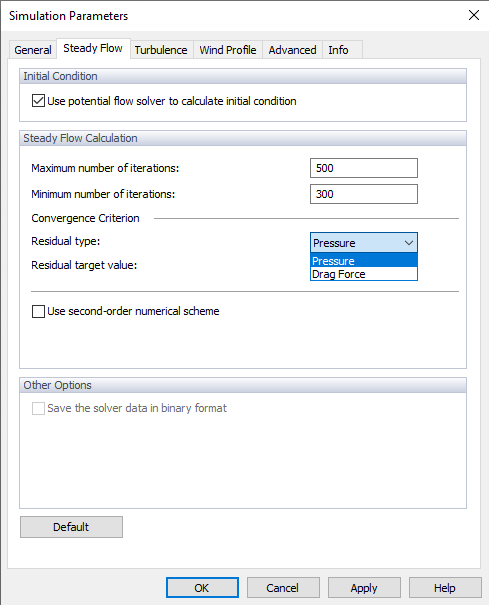
'Kryterium zbieżności' stanowi wartość graniczną dla obliczeń. Dostępne są dwa kryteria zbieżności, kryterium ciśnienia lub kryterium siły oporu. Należy wybrać jedną z opcji w Typie pozostałości, a następnie ustawić wartość docelową.

Parametry symulacji, ustalony przepływ, typ pozostałości

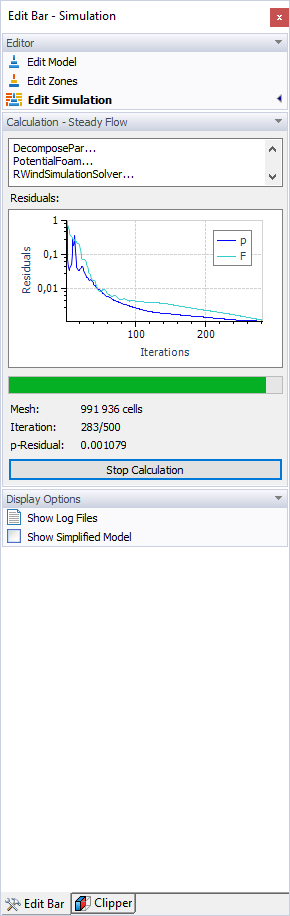
Jeżeli ilość pozostałości spadnie poniżej zdefiniowanej wartości, obliczenia zostają zakończone. Podczas obliczeń wyświetlany jest wykres iteracji i ilości resztkowej (p-Residual dla ciśnienia). Jest ona również dostępna w wynikach symulacji (patrz rozdział Wartości rezydualne).

Wykres obliczeń

Pole wyboru "Zastosować schemat numeryczny drugiego rzędu" określa, który schemat numeryczny zostanie zastosowany dla składników dywergencji (strumieni). Domyślnie nie jest aktywna, więc obliczenia są przeprowadzane według pierwszego rzędu. Jeżeli pole wyboru jest zaznaczone, rozwiązywanie problemów jest wykonywane według drugiego rzędu.

Inne opcje

Solwer stanu ustalonego w RWIND 3 nie uwzględnia w pełni efektów "oscylacyjnych", jak opisano w FAQ 4731. Aby numerycznie rozwiązywać równania różniczkowe cząstkowe, należy zdyskretyzować wszystkie człony różniczkowe (pochodne przestrzenne i czasowe). Więcej informacji na temat solwerów można znaleźć w dokumentacji Algorytmy i solwery. Istnieje długa lista dyskretyzacji ("schematy"), z których każdy ma określone zachowanie numeryczne ze względu na dokładność, stateczność i zbieżność. Więcej informacji na temat zbieżności można znaleźć na stronie CFD Direct.