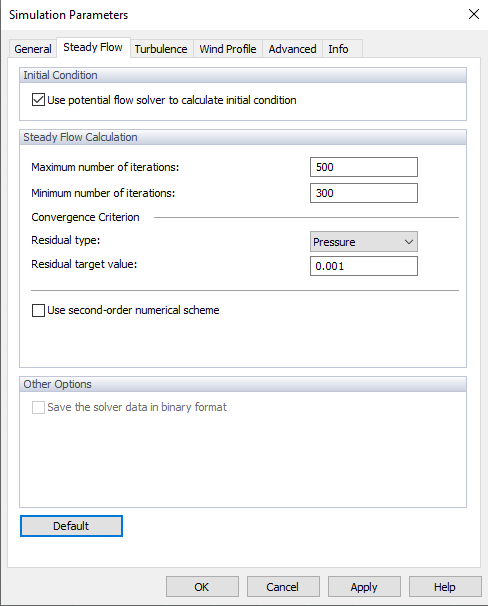
Die Berechnung der stationären Strömung kann im Register "Allgemein" des Dialogs "Simulationsparameter" ausgewählt werden (siehe Bild Simulationsparameter ).
Anfangsbedingungen
Bei Aktivierung der Option "Anfangsbedingung mit Potentialströmung berechnen" wird eine linearisierte Version der nicht-viskosen Navier-Stokes-Gleichungen zur Erzeugung der Anfangsbedingungen verwendet.
Berechnung der stationären Strömung
Sie können die "Maximale Anzahl der Iterationen" festlegen. Standardmäßig liegt die Grenze bei 500 Iterationen. Wenn die Berechnung in weniger Iterationen konvergiert, wird sie beendet. Sie können auch die "Mindestanzahl der Iterationen" festlegen, die standardmäßig auf 300 Iterationen eingestellt ist (siehe Bild Programmoptionen ), unabhängig davon, ob das Konvergenzkriterium (siehe unten) bereits erfüllt ist. Die maximale Anzahl ist sinnvoll, um Endlosschleifen zu vermeiden.
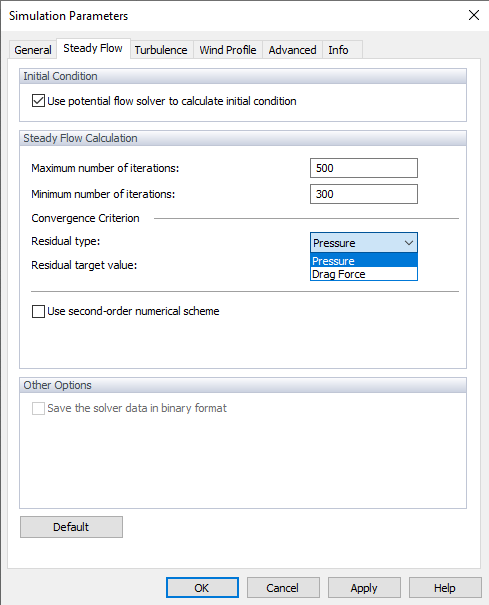
Das "Konvergenzkriterium" stellt die Stoppgrenze für die Berechnung dar. Es stehen zwei Konvergenzkriterien zur Verfügung; Sie können dem Druckkriterium oder dem Widerstandskraftkriterium folgen. Wählen Sie eine der Optionen im Differenztyp und legen Sie dann den Zielwert fest.
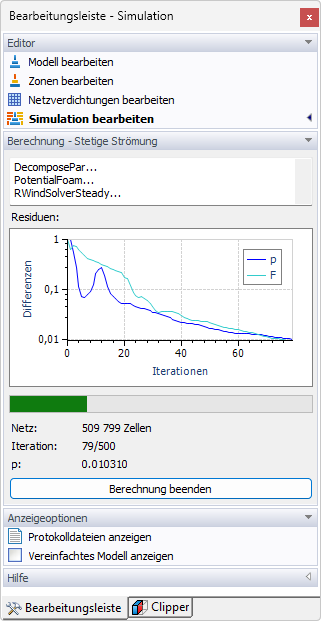
Sobald die Differenzmenge den definierten Wert unterschreitet, wird die Berechnung abgebrochen. Das Diagramm der Iterationen und der Differenzmenge (p-Differenz für Druck) wird während der Berechnung angezeigt. Es ist auch in den Simulationsergebnissen verfügbar (siehe Kapitel Residuen).
Das Kontrollfeld "Numerisches Schema zweiter Ordnung verwenden" steuert, welches numerische Schema für Divergenzterme (Flüsse) verwendet wird. Es ist standardmäßig nicht aktiviert, so dass die Berechnung nach der ersten Ordnung durchgeführt wird. Wenn das Kontrollfeld aktiviert ist, wird die Berechnung nach zweiter Ordnung durchgeführt.
Sonstige Optionen
Der stationäre Solver von RWIND 3 erfasst nicht vollständig die "oszillierenden" Effekte, wie sie in FAQ 4731 beschrieben sind. Um die partiellen Differentialgleichungen numerisch zu lösen, müssen alle Differentialterme (räumliche und zeitliche Ableitungen) diskretisiert werden. Weitere Informationen über Solver finden Sie in der Dokumentation über Algorithmen und Solver. Es gibt zahlreiche Diskretisierungen („Schemata“), wobei jedes Schema ein bestimmtes numerisches Verhalten in Bezug auf Genauigkeit, Stabilität und Konvergenz aufweist. Weitere Informationen über die Konvergenz finden Sie bei CFD Direct.