Update NDS 2018 für Brettsperrholzbemessung

Neuregelung 1: Formatkonvertierungsfaktor, K_F (nur LRFD) - Abschnitt 10.3.10

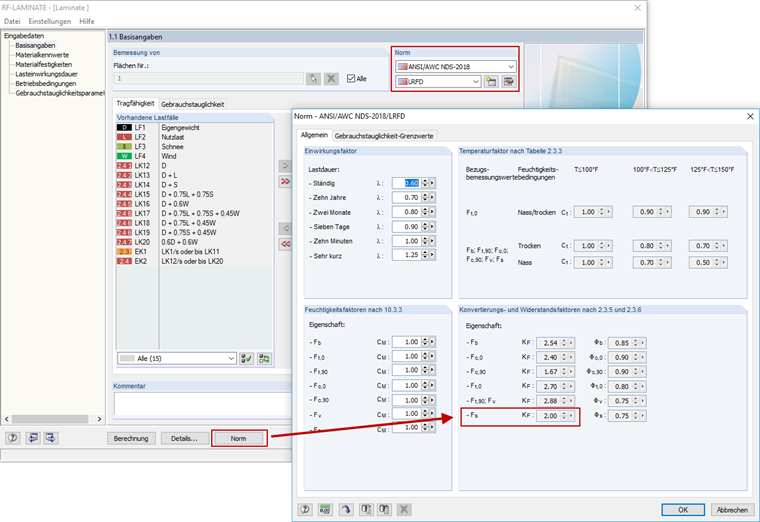
Der Formatkonvertierungsfaktor K_F wird in Tabelle 10.3.1 [1] näher erläutert. Dieser Wert wird in Betracht gezogen, wenn die Rollschubkraft F_s mit LRFD allein berechnet wird. Der Faktor passt den ASD-Referenzbemessungswert an den LRFD-Referenzwiderstand an. Vorher war der Faktor mit 2,88 im NDS von 2015 angesetzt. In der Version von 2018 wurde dieser Wert zu 2,00 korrigiert.

The RF-LAMINATE module has been updated to account for the new K_F factor of 2.00 when designing as per ANSI/AWC NDS-2018 and LRFD.

Formatkonvertierungsfaktor KF bei Bemessung nach NDS 2018 und LRFD in RF-LAMINATE

Neuregelung 2: Auftretende Biegesteifigkeit für Durchbiegungsberechnungen - Abschnitt 10.4.1

The 2018 NDS states in Section 10.4.1 [1] that the deflection of a CLT panel must include the effects of bending as well as shear deformation. Die Norm empfiehlt darüber hinaus, die effektive Biegungssteifigkeit EI_eff zu reduzieren, um die Schubverformung als eine Funktion der Plattenlast sowie Lagerbedingungen, Geometrie, Spannweite und effektive Schubsteifigkeit zu berücksichtigen. The stiffness adjusted for shear deformation is referred to as the apparent bending stiffness, (EI)_app, and can be calculated as per equation 10.4-1 [1]. Diese Gleichung weicht etwas von der Norm von 2015 ab.

In RFEM und RF-LAMINATE ist es nicht möglich (EI)_app zu berücksichtigen, da der Anpassungsfaktor der Schubverformung  K_s für jede Platte mit Tabelle 10.4.1.1 [1] bestimmt werden muss. K_s depends on both the loading conditions (that is, uniformly distributed, line load at mid-span, line load at quarter points, and so on), as well as the end fixity (that is, fixed, pinned, cantilever, and so on). These variables do not necessarily fall into the defined categories defined in Table 10.4.1.1, but rather may include several different loading conditions or end fixity. Daher gibt es bei RF-LAMINATE einen anderen und genaueren Ansatz, um die Effekte der Schubverformung zu berücksichtigen.

RF-LAMINATE wendet die Laminattheorie an, um die effektive Schubsteifigkeit einer BSH-Platte zu berechnen. Die gesamte Steifigkeitsmatrix für jede Platte besteht aus mehreren Steifigkeitseingaben, die Biegung und Torsion, Schub, Membrane und Exzentrizität beinhalten, zusammen mit den D₄₄ and D₅₅-Eingaben, die sich speziell auf Schubsteifigkeit beziehen.

Schubsteifigkeitseingaben D44 und D55 in der gesamten Steifigkeitsmatrix der BSH-Platte:

General technical regulations [2] suggest that in order to calculate the effective shear stiffness, the shear stiffness must be reduced by applying a shear correction coefficient, κ, in the panel's x and y directions. Effektive Schubsteifigkeit = κGA
mit
κ = Schubkorrekturfaktor
G = Schubmodul
A = Querschnittsfläche

Für ein typisches homogenes Material hat der Schubspannungsverlauf eine Parabelform, wenn der Querschnitt des Elements betrachtet wird. Ein κ-Wert von 5/6 oder 0,8 wird typischerweise für dieses homogene Material verwendet. However, when looking at the shear stress distribution of a CLT panel, the shape is no longer parabolic and the material is not considered homogeneous, but rather isotropic. Daher kann der Faktor 0,8 nicht verwendet werden. Es gibt einige Schätzungen für den Schubkorrekturbeiwert für BSH-Platten, die von der Anzahl an Querlagen abhängig sind.

Schätzungen Schubspannungsverlauf und Schubkorrekturfaktor

In RF-LAMINATE wird der Schubkorrekturfaktor indirekt berücksichtigt, wenn die D₄₄- und D₅₅-Steifigkeitsmatrixeinträge nach der Grashofschen Integralformel [3] berechnet werden.

Die Werte der Steifigkeiten D₄₄, D₅₅ werden durch die folgenden Gleichungen angegeben, wobei l die durchschnittliche Länge der Linien ist, die die Fläche als eine "Box" umgeben.

Die Einträge D₄₄ und D₅₅, die automatisch in RF-LAMINATE berechnet wurden, werden nun die erforderlichen Schubsteifigkeitsreduzierungen berücksichtigen. Die gleiche Steifigkeitsmatrix wird weiter in RFEM benutzt, um die Plattendurchbiegungen zu berechnen. Therefore, the requirements of the 2018 NDS considering both bending and shear deformation for deflection calculations as per Section 10.4.1 are met by taking a more exact approach with the Laminate Theory, as opposed to approximating the effects of shear deformation by reducing the effective bending stiffness.