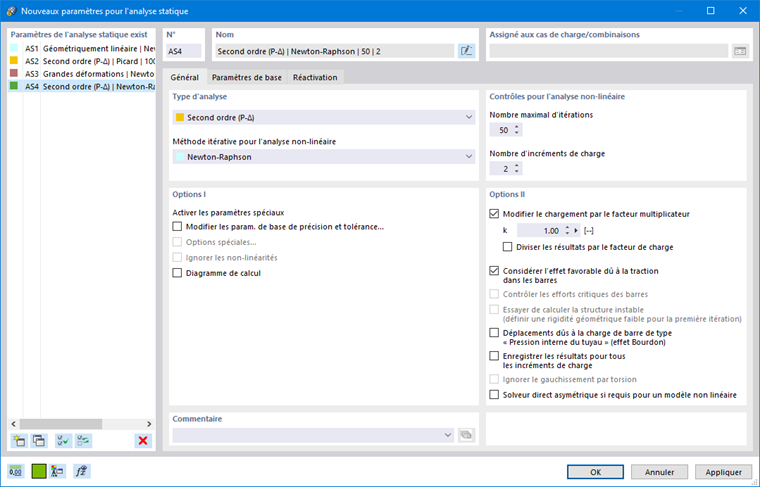
Un paramètre pour l'analyse statique (SA) définit les règles selon lesquelles les cas de charge et les combinaisons de charges sont calculés.
Types d'analyse
Dans RFEM et RSTAB, trois types d'analyse standard sont prédéfinis :
- Analyse géométriquement linéaire
Lors du calcul selon l'analyse géométriquement linéaire (premier ordre), l'équilibre est analysé sur une structure non déformée.
- Second ordre
Dans la théorie « structurale » du second ordre, l'équilibre est déterminé sur un système structural déformé. Des déformations sont supposées petites.
- Analyse des grandes déformations
L'analyse des grandes déformations (selon la théorie du troisième ordre) prend en compte les efforts longitudinaux et transversaux dans le calcul. Après chaque étape d'itération, la matrice de rigidité du système déformé est générée.
Méthode itérative pour l'analyse non linéaire
Selon le type d'analyse, il existe différentes méthodes pour résoudre le système d'équations algébriques non linéaires.
- Newton-Raphson
L'approche selon Newton-Raphson est prédéfinie pour l'analyse des grandes déformations. Le système d'équations non linéaire est résolu numériquement à travers des approximations itératives avec tangentes.
- Selon Picard
La méthode de Picard peut être comprise comme une approximation finie de la méthode de Newton-Raphson. La différence entre l'itération actuelle et l'itération d'origine dans l'étape d'augmentation de charge actuelle est considérée.
- Newton-Raphson combiné avec Picard
Avec cette méthode, la méthode selon Picard est appliquée en premier. Après quelques itérations, le programme passe à la méthode selon Newton-Raphson.
- Newton-Raphson avec analyse post-critique
Cette méthode est utile pour résoudre les problèmes selon l'analyse post-critique qui nécessitent de surmonter une zone d'instabilité.
- Relaxation dynamique
La méthode finale est appropriée pour les calculs selon l'analyse des grandes déformations et pour la résolution de problèmes selon l'analyse post-critique. Dans cette approche, un paramètre de temps artificiel est introduit. En considérant l'inertie et l'amortissement, l'échec peut être pris comme un problème dynamique.