Ein Berechnungsabbruch wegen eines instabilen Systems kann verschiedene Gründe haben. Einerseits kann er auf eine „reelle“ Instabilität aufgrund einer Überlastung des Systems hinweisen, anderseits können jedoch auch Modellierungsungenauigkeiten für diese Fehlermeldung verantwortlich sein. Nachstehend finden Sie eine mögliche Vorgehensweise, um die Ursache der Instabilität ausfindig zu machen.
1. Kontrolle der Modellierung
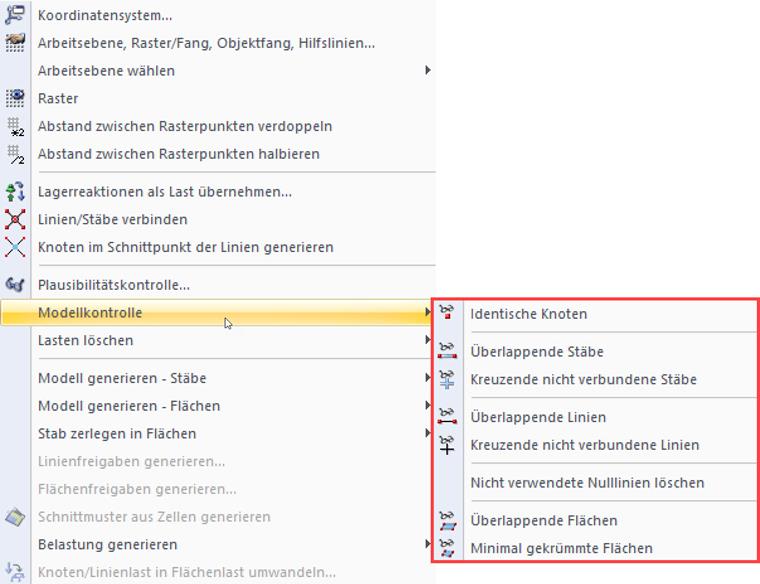
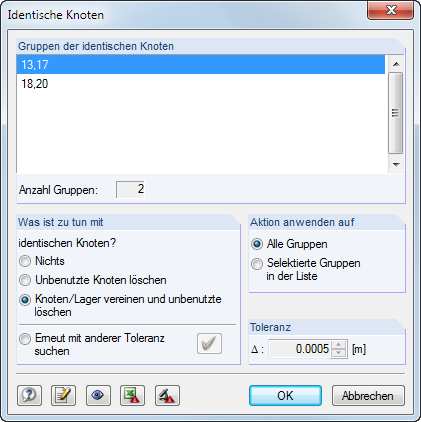
Zuerst sollten Sie überprüfen, ob das System vonseiten der Modellierung in Ordnung ist. Hierfür bietet es sich an, die von RFEM 5 / RSTAB 8 zur Verfügung gestellten Modellkontrollen (Extras → Modellkontrolle) zu verwenden. Mithilfe dieser Möglichkeiten lassen sich beispielsweise identische Knoten und überlappende Stäbe finden und gegebenenfalls löschen.
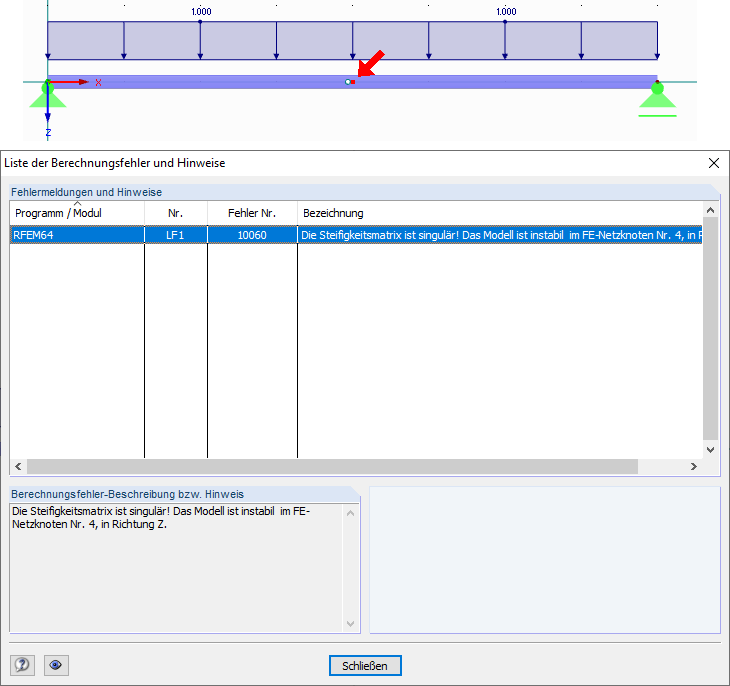
Weiterhin kann man die Struktur z. B. unter reinem Eigengewicht in einem Lastfall nach Theorie I. Ordnung berechnen. Werden hier Ergebnisse ausgegeben, ist die Struktur hinsichtlich der Modellierung stabil. Sollte dies nicht der Fall sein, sind im Folgenden die häufigsten Ursachen aufgelistet (siehe auch Video "Modellkontrolle" im Bereich "Downloads):
Falsche Definition von Auflagern / Fehlen von Auflagern
Dies kann zu Instabilitäten führen, da das System nicht in alle Richtungen gehalten ist. Deshalb ist es erforderlich, dass die Lagerbedingungen mit dem System als auch mit den äußeren Randbedingungen im Gleichgewicht stehen. Statisch unterbestimmte Systeme können ebenfalls zu Berechnungsabbrüchen aufgrund mangelnder Randbedingungen führen.
Torsion von Stäben um die eigene Achse
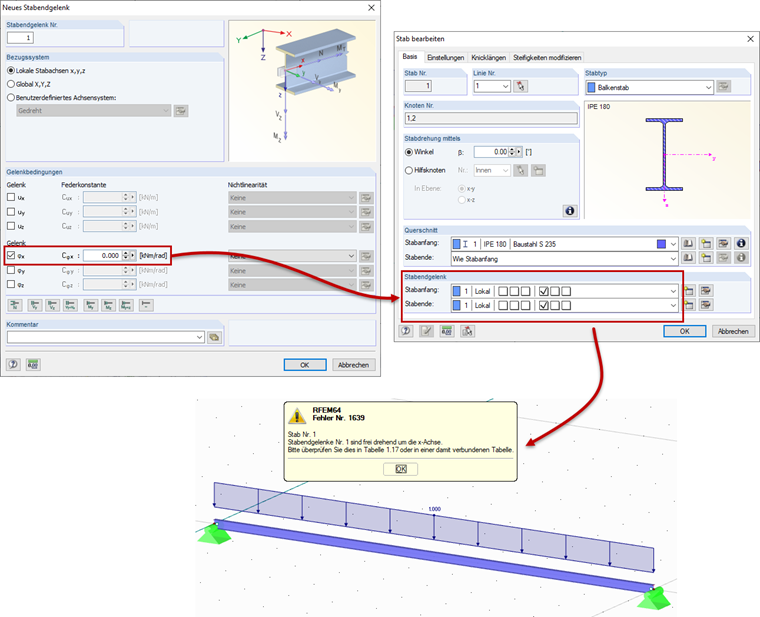
Wenn Stäbe um die eigene Achse tordieren, also der Stab um die eigene Achse nicht gehalten ist, kann dies zu Instabilitäten führen. Häufig liegt die Ursache an den Einstellungen der Stabendgelenke. So kann es sein, dass sowohl am Anfangs- als auch am Endknoten Torsionsgelenke eingeführt wurden. Ein Hinweisfenster beim Start der Berechnungen macht den Nutzer dabei allerdings aufmerksam.
Fehlende Verbindung von Stäben
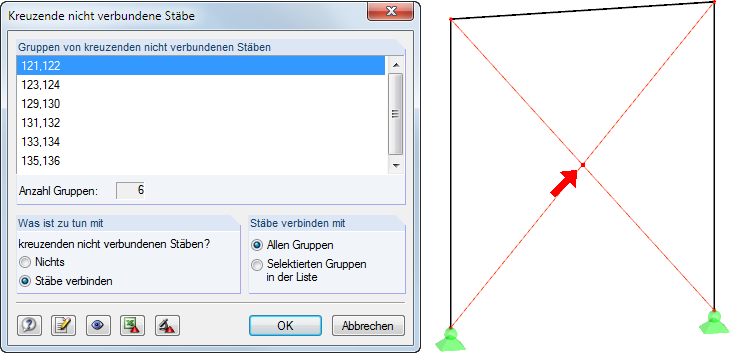
Vor allem bei größeren und komplexeren Modellen kann es schnell passieren, dass einige Stäbe nicht miteinander verbunden sind und somit "frei in der Luft schweben". Auch das Vergessen von kreuzenden Stäben, die sich eigentlich miteinander schneiden sollten, können zu Instabilitäten führen. Eine Abhilfe schafft die Modellkontrolle "Kreuzende, nicht verbundene Stäbe", die nach Stäben sucht, die sich kreuzen, jedoch keinen gemeinsamen Knoten im Schnittpunkt aufweisen.
Kein gemeinsamer Knoten
Die Knoten liegen augenscheinlich an selber Stelle, bei genauerer Betrachtung weichen diese jedoch minimal voneinander ab. Häufige Ursachen sind CAD-Importe, die man aber mithilfe der Modellkontrolle bereinigen kann.
Entstehen einer Gelenkkette
Zu viele Stabendgelenke an einem Knoten können eine Gelenkkette verursachen, die zu einem Berechnungsabbruch führt. Pro Knoten dürfen nur n-1 Gelenke mit demselben Freiheitsgrad bezogen auf des globale Koordinatensystem definiert werden, wobei "n" die Anzahl der angeschlossenen Stäbe ist. Selbiges gilt auch für Liniengelenke.
2. Kontrolle der Aussteifung
Eine fehlende Aussteifung führt ebenfalls zu Berechnungsabbrüchen infolge von Instabilitäten. Daher sollte immer kontrolliert werden, ob das Tragwerk in allen Richtungen ausreichend ausgesteift ist.
3. Numerische Probleme
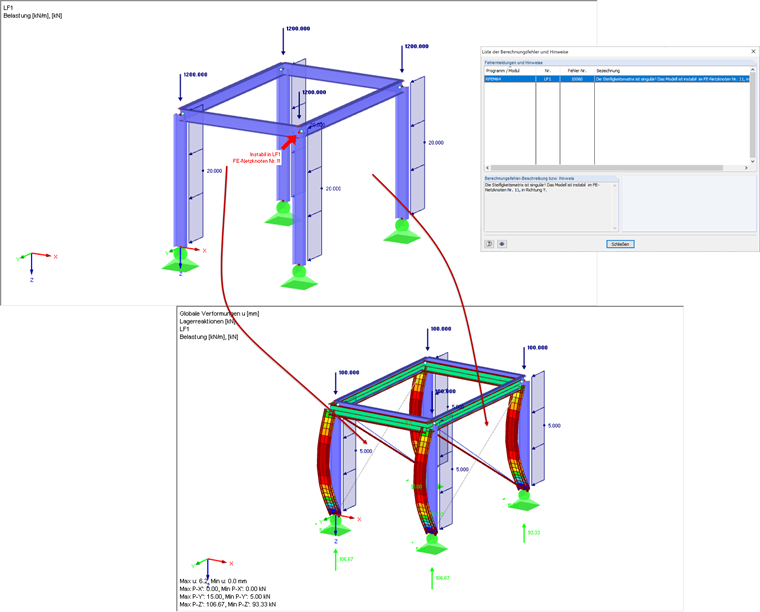
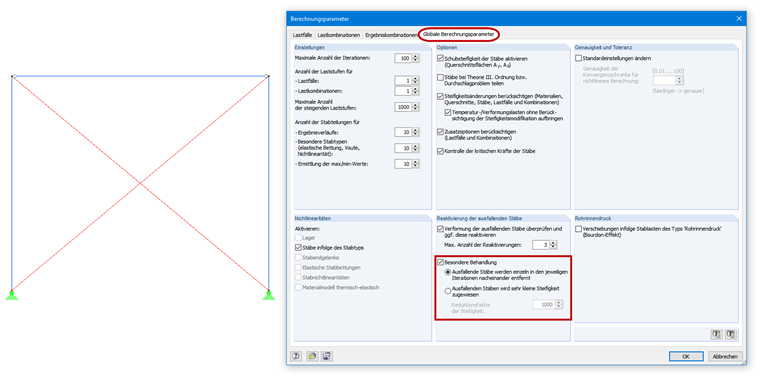
Zu diesem Punkt wird in Bild 08 ein Beispiel aufgezeigt. Es handelt sich um einen gelenkigen Rahmen, welcher durch Zugstäbe ausgesteift wird. Wegen der Stielverkürzungen infolge der Vertikallasten erhalten die Zugstäbe im ersten Berechnungsdurchgang kleine Druckkräfte. Sie werden aus dem System entfernt (da nur Zug aufgenommen werden kann). Im zweiten Rechendurchgang ist das Modell ohne diese Zugstäbe dann instabil. Es gibt mehrere Möglichkeiten, dieses Problem zu lösen. Sie können den Zugstäben eine Vorspannung (Stablast) erteilen, um die kleinen Druckkräfte zu „eliminieren“, den Stäben eine kleine Steifigkeit zuweisen oder die Stäbe nacheinander in der Berechnung entfernen lassen (siehe Bild 08).
4. Ursachenfindung einer Instabilität
Automatische Modellkontrolle mit grafischer Ausgabe
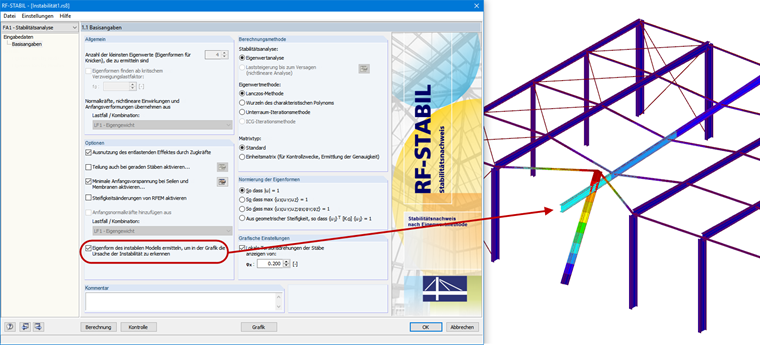
Um eine grafische Darstellung der Ursache einer Instabilität zu erhalten, kann das Modul RF-STABIL (für RFEM 5) bzw. das Add-On Strukturstabilität (für RFEM 6) weiterhelfen. Mit der Option "Eigenform des instabilen Modells ermitteln" (siehe Bild 09) bzw. "Berechnen ohne Belastung für Instabilitätsnachweis durch Eigenform" lassen sich vermeintlich instabile Systeme berechnen. Es wird anhand der Strukturdaten eine Eigenwertanalyse durchgeführt, sodass als Ergebnis die Instabilität des betroffenen Bauteils grafisch dargestellt wird.
Verzweigungsproblem
Lassen sich Lastfälle oder Lastkombinationen nach Theorie I. Ordnung berechnen und die Berechnung steigt erst ab Theorie II. Ordnung aus, so liegt ein Stabilitätsproblem vor (Verzweigungslastfaktor kleiner 1,00). Der Verzweigungslastfaktor gibt an, mit welchem Faktor die Belastung multipliziert werden muss, damit das Modell unter der zugehörigen Last instabil wird (z. B. ausknickt). Daraus folgt: Ein Verzweigungslastfaktor kleiner 1,00 bedeutet, dass das System instabil ist. Nur ein positiver Verzweigungslastfaktor größer 1,00 lässt die Aussage zu, dass die Belastung infolge der vorgegebenen Normalkräfte multipliziert mit diesem Faktor zum Knickversagen des stabilen Systems führt. Um die "Schwachstelle" ausfindig machen zu können, empfiehlt sich folgende Vorgehensweise, welche das Modul RSKNICK (RSTAB 8) oder RF-STABIL (RFEM 5) bzw. das Add-On Strukturstabilität (RFEM 6 / RSTAB 9) voraussetzt (siehe auch Video "Verzweigungsproblem" im Bereich "Downloads).
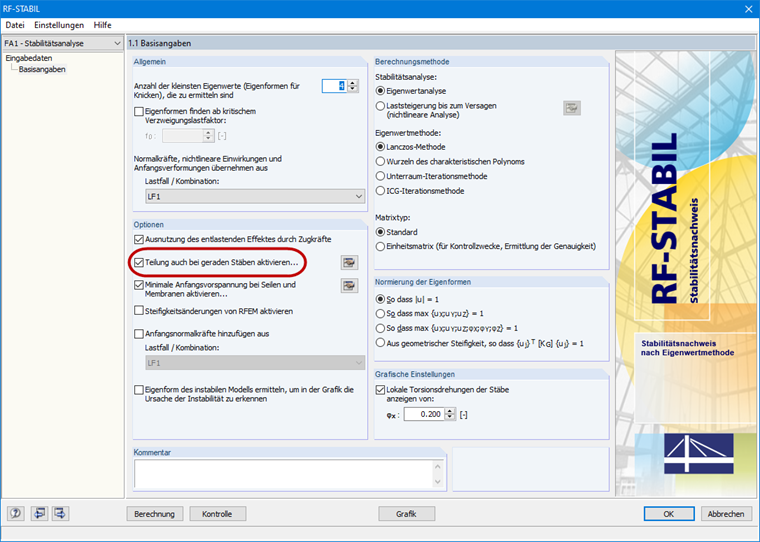
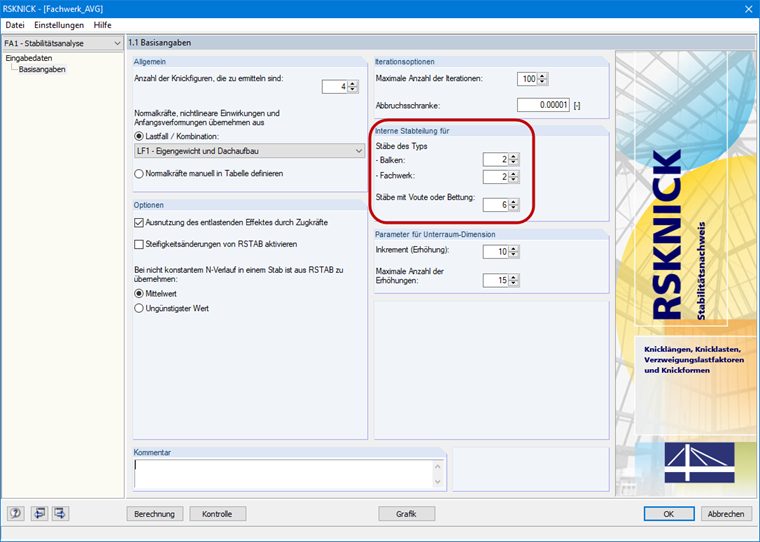
Zuerst sollte die Last der betroffenen Lastkombination solange verringert werden, bis die Lastkombination stabil wird. Als Hilfsmittel dient dabei der Lastfaktor in den Berechnungsparametern der Lastkombination. Dies entspricht auch einer manuellen Ermittlung des Verzweigungslastfaktors, falls die oben genannten Module bzw. Add-Ons nicht zur Verfügung stehen. Bei rein linearen Strukturelementen kann es bereits ausreichen, die Lastkombination nach Theorie I. Ordnung zu berechnen und diese im Zusatzmodul direkt zu berechnen bzw. die Verzweigungslast mit dem Add-On ermitteln zu lassen. Anhand der grafischen Knick- oder Beulfigur dieser Lastkombination können Sie möglicherweise die "Schwachstelle" im System ausfindig ausmachen und Abhilfemaßnahmen ergreifen. Damit neben den globalen Eigenformen auch die lokalen Versagensformen der Stäbe erfasst werden, sollten Sie im Modul RF-STABIL (RFEM 5) die Stabteilung aktivieren bzw. im Modul RSKNICK (RSTAB 8) die Teilung für Fachwerkstäbe auf mindestens "2" setzen. Für das Add-On Strukturstabilität (RFEM 6 / RSTAB 9) sollten Sie überprüfen, ob die Stabteilungen für Stäbe aktiviert sind.
Siehe Links unter diesen FAQ.