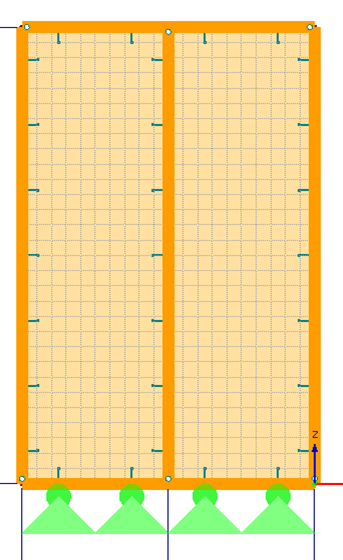
Aufbau Holztafelwand
Die Ermittlung der Tragfähigkeit einer Holztafelwand erfolgt gemäß den Regelwerken wie zum Beispiel Eurocode 5 oder NDS 2018. In vielen Ländern hat sich die Schubfeldtheorie zur Bemessung durchgesetzt.
Wie eingangs erwähnt, ist die Bemessung der Holztafeln nicht das Hauptaugenmerk dieser Betrachtung. Sie wird daher im Folgenden nur kurz nach dem im Eurocode 5 geregelten Verfahren beschrieben. Ebenfalls wird es im Rahmen dieser Beiträge keine umfassenden Hinweise zu den geometrischen Regelungen oder Mindestabständen der Verbindungsmittel geben.
Eine Holztafelwand besteht aus folgenden Elementen:
- Kopfrippe
- gegebenenfalls Innenrippe
- Beplankung
- Verbindungsmittel
- Randrippe
- Fußrippe
Tragfähigkeit
Üblicherweise erfolgt die Verbindung der Beplankung aus OSB mit den Rippen über Klammern.
Tragfähigkeit eines Verbindungsmittels:
Gleichung 1:
Fließmoment My,Rk = 150 ⋅ d3
Gleichung 2:
Lochleibungsfestigkeit fh,1,k = 65 ⋅ d-0,7 ⋅ t0,1
;fh,2,k = 0,082⋅ρk ⋅ d-0,3
Gleichung 3:
Tragfähigkeit (NA.109 DIN EN 1995-1-1)
mit
d = Durchmesser Verbindungsmittel
t = Stärke Beplankung
Gleichung 4:
Verhältnis Wandbreite
Gleichung 5:
Tragfähigkeit
mit
bi = Gesamtbreite der Wand
h = Wandhöhe
b0 =
av = Abstand Verbindungsmittel
Weitere wichtige Nachweise sind zum Beispiel der Knicknachweis der Randrippen, Nachweis der Verankerung und der Beulnachweis der Beplankung.
Verformung
Analog zum Nachweis der Tragfähigkeit sind auch bei der Ermittlung der Steifigkeit zur Berechnung der Verformung die vier Elemente einer Holztafel relevant:
- Nachgiebigkeit aus dem Verbindungsmittel
- Nachgiebigkeit aus der Beplankung
- Nachgiebigkeit der Rippen
- Nachgiebigkeit der Verankerung
Gleichung 6:
Nachgiebigkeit des Verbindungsmittels (Klammer)
Gleichung 7:
Nachgiebigkeit der Beplankung
Gleichung 8:
Nachgiebigkeit der Rippen
Zusammenfassung
In diesem Beitrag wurde die Ermittlung der Tragfähigkeit sowie der Steifigkeit einer Holztafelwand aufgezeigt. In den folgenden Beiträgen zum Thema Holztafeln wird anhand dieser Grundlagen die Berücksichtigung dieser Steifigkeiten in einer zwei- beziehungsweise dreidimensionalen Berechnung erläutert.
.jpg?mw=350&hash=8f312d6c75a747d88bf9d0f5b1038595900b96c1)
.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)
