Üblicherweise gelten Bauwerke als nicht schwingungsanfällig, wenn die Verformungen unter Windeinwirkung durch Böenresonanz um nicht mehr als 10 % vergrößert werden [2]. In diesem Fall kann man die zeitlich veränderliche Windeinwirkung als statische Ersatzlast beschreiben.
Unter der Annahme, dass die im Windstrom enthaltenen Wirbel im Verhältnis zur Gebäudeabmessung sehr groß sind, kann mit RWIND Simulation nach der "Quasi-stationären Methode" beziehungsweise dem sogenannten Böenkonzept eine statisch wirkende Druckverteilung p auf eine Gebäudegeometrie berechnet werden [3].
Dabei wird im Grunde für die turbulente Geschwindigkeitsschwankung über die Wirkdauer der Böe ein stationäres Strömungsfeld um das Bauwerks-Modell angenommen [3]. Die Druckschwankung an der Modelloberfläche aus der Anströmturbulenz wird damit als Zustand stationär über einen bestimmten Zeitraum t gesehen. Die Fluktuationen folgen somit exakt dem Verlauf der zeitlich gemittelten Druckbeiwerte cp,mean auf der Modelloberfläche.
Der daraus resultierende windinduzierte Druck Δp(t) auf die Modelloberflächen hängt dann rein von der Anströmgeschwindigkeit v(t) ab.
|
ρ |
Dichte der Luft |
|
v |
Anströmgeschwindigkeit |
|
cp,mean |
Zeitlich gemittelter Druckbeiwert |
|
t |
Zeit |
Der Betrag des Anströmgeschwindigkeitsvektors v(t) ist dann:
v(t)² = (vx,mean + vx,fluctuation(t))² + vy,fluctuation(t)² + vz,fluctuation(t)²
Wenn die quadrierten Terme nur einen geringen Beitrag leisten, ergibt sich ein effektiver Betrag des Anströmgeschwindigkeitsvektors v(t):
v(t)² = vx,mean² + 2 ⋅ vx,mean ⋅ vx,fluctuation(t)
Mit Nutzung der effektiven Anströmgeschwindigkeit in der Gleichung des windinduzierten Drucks ergibt sich:
Δp(t) = 1/2 ⋅ ρ ⋅ vx,mean² [1 + (2 ⋅ vx,fluctuation(t)) / vx,mean] ⋅ cp,mean
Diese Umformung zeigt, dass die Schwankung des Winddrucks Δp(t) nur noch von der Schwankung der Windgeschwindigkeit vx,fluctuation(t) in die Hauptanströmrichtung x abhängt.
Ersetzt man die zeitlich veränderlichen Geschwindigkeitsschwankung vx,fluctuation(t) durch die maximal auftretenden Geschwindigkeitsschwankung vx,fluctuation,max, nimmt man die zeitliche Veränderlichkeit aus dem System.
Vergleicht man dann den Term vx,fluctuation,max / vx,mean als ein Vielfaches g der Turbulenzintensität Iv(z),
|
δv |
Standardabweichung zur mittleren Geschwindigkeit vmean |
|
vmean(z) |
Mittlere Geschwindigkeit abhängig von der Höhe |
|
z |
Höhe über Grund |
kann man den Term in der eckigen Klammer als Böenfaktor G(z) beschreiben. Mit Einsetzen der Terme in die Nennwindlastgleichung ergibt sich:
|
ρ |
Dichte der Luft |
|
vmean |
Mittlere Anströmgeschwindigkeit |
|
G(z) |
Böenfaktor abhängig von der Höhe |
|
cp,mean |
Zeitlich gemittelter Druckbeiwert |
mit
|
g |
Faktor zur Festlegung der Böendauer |
|
Iv(z) |
Turbulenzintensität abhängig von der Höhe |
|
z |
Höhe über Grund |
Beispielsweise ist in der EN 1991-1-4 der Faktor g zur Beschreibung der Böendauer 3,5.
RWIND Simulation berechnet die Mittelwerte der Drücke pmean auf der Modelloberfläche abhängig von einer Anströmgeschwindigkeit vx(z) über eine stationäre Lösung der RANS-Gleichungen durch Anwendung des SIMPLEC-Algorithmus. Da hier die Mittelwerte der Druckbeiwerte cp,mean auf dem Verhältnis zwischen ermittelten Druckmittelwerten pmean zu dem ungestörten Spitzenwindgeschwindigkeitsdruck an der Dachhöhe q(Dachhöhe) basieren,
cp,mean = pmean / q(Dachhöhe)
kann zur Ermittlung der Nennwindlasten nach dem Böenkonzept die Anströmgeschwindigkeit aus dem umgerechneten Spitzenwindgeschwindigkeitsdruck q(z) über die Höhe verwendet werden [1].
v(z) = √(2 ⋅ q(z) / ρ)
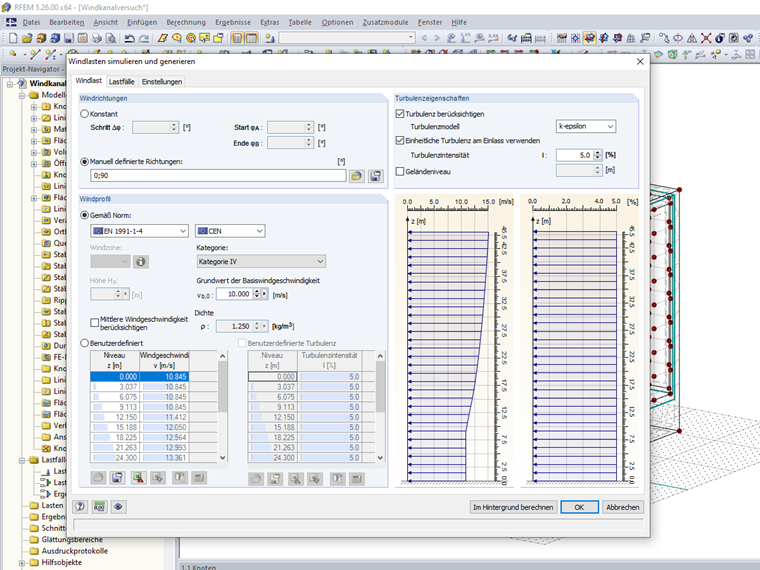
Diese Windgeschwindigkeit beinhaltet damit die mittlere Windgeschwindigkeit vmean und den maximalen Schwankungsanteil vfluctuation. Die Anströmturbulenzintensität kann in diesem Fall konstant über die Höhe sehr klein auf zirka 5 % eingestellt werden [4].
Bei Betrachtungen von Kraftwirkungen auf das gesamte Gebäude oder große Flächenbereiche liefert diese Methode eine sehr gute Näherung zur natürlichen Windbelastung [3]. Die Ursache liegt darin, dass die durch die Mittelung ausgeblendeten kleinen Turbulenzeffekte nur in Teilbereichen wirken und durch die globale Aufintegration der Kraftgrößen keinen merklichen Effekt mit sich bringen.
Weiter reagiert das Konzept auch bei kleinen Teilflächen mit frontaler Anströmung sehr gutmütig, da hier die effektiven Druckschwankungen bereits sehr gut im Spitzenwindgeschwindigkeitsprofil erfasst sind [3].
Dem entgegen ergibt das System bei Flächen mit Strömungsablösungen (Seiten- und Rückwand) eine schlechtere Konvergenz an die Realität. Genau an diesen Regionen hat die durch das Böenkonzept "weggemittelte" gebäudeinduzierte Turbulenz einen größeren Effekt als der im Anströmgeschwindigkeitsprofil enthaltene Anströmturbulenzeffekt.